相对论中的质空积守恒

殷 建,殷 业

(1.无锡职业技术学院基础课教学部,江苏 无锡 214121; 2.上海师范大学信息与机电工程学院,上海 200234)

相对论中的质空积守恒

殷 建1,殷 业2

(1.无锡职业技术学院基础课教学部,江苏 无锡 214121; 2.上海师范大学信息与机电工程学院,上海 200234)

相对论中不同的参照系有不同的时空度量和质量度量,当测量从相对物体静止的参照系变到相对物体运动的参照系时对物体度量的体积会变小,质量会增加,在物体的体积变小和质量增加之间是否存在数量上的内在联系,文章研究了该问题,并在相对论中证明了它们之间的关系遵循:质空积守恒,同时证明质空积不但对惯性系守恒而且对平移非惯性系也守恒。文中还分析了质空积守恒和能量守恒的关系,发现质空积守恒是能量守恒的更高级形式。

相对论;质空积;质空积守恒;真空能;能量守恒

相对论中不同的参照系有不同的时空度量和质量度量,爱因斯坦在第一篇关于相对论的论文中就指出一个相对地面高速运动的球从地面观察是一个椭球[1]。也即从与球一起运动的参照系测量变到地面参照系测量,球的体积会缩小,但质量会增大,那么在体积缩小和质量增大之间存不存在数量上的内在联系?本文研究了该问题,并在相对论中证明了它们之间的关系遵循:质空积守恒,同时证明质空积不但对惯性系守恒而且对平移非惯性系也守恒。根据爱因斯坦的质能关系公式 ,质量是一种储能形式,当质量变化时必伴随着能量的变化,本文分析了质空积守恒和能量守恒的关系,发现质空积守恒是能量守恒的更高级形式。

1 相对论中不同参照系对物体体积和质量的度量

爱因斯坦在“论动体的电动力学”[1]中指出,经典物理学在解释运动物体的电磁现象时会表现出不对称,为了解决这一矛盾,爱因斯坦选择了洛伦兹变换,因为洛伦兹变换对麦克斯韦方程组是协变的,这样就解决了电动力学中的所有不对称现象。

洛伦兹变换为:

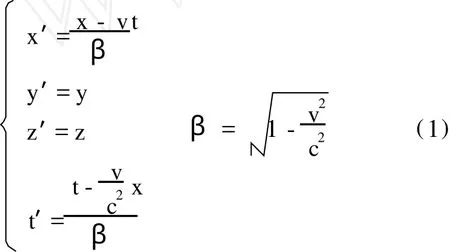
其中 K系为 (O xyzt)和 K′系为 (O′x′y′z′t′), K′相对 K沿 x轴正向匀速运动。

至此狭义相对论的建立只剩一个问题,如何导出洛伦兹变换?洛伦兹得到洛伦兹变换是为了使他的电子论可以解释新的实验事实[2],特别是迈克尔逊 -莫雷实验。也就是洛伦兹变换的获得并不是为了满足方程的坐标系协变性。爱因斯坦为了得到洛伦兹变换,进行了革命性的思考:1)绝对的运动不存在,只存在相当运动;2)宁可牺牲同时性,也要保证规律的协变性;3)欧几里得:“公理 +逻辑 =理论”的方法可以用来建构新力学,这种方法爱因斯坦称为“原理理论”[3]。基于这样的哲学思考爱因斯坦建立了两条公设:1)光速不变原理。2)狭义相对性原理。并从这两条公设出发,通过简单的逻辑推理得到了洛伦兹变换[4],至此爱因斯坦建立了狭义相对论。

下面我们讨论运动尺变短和运动物体体积变小的问题。

从洛仑兹变换(1)可得在 K和 K′中度量尺的长度,有长度缩短的相对论效应。其公式如下:

其中:l为 K系中测量的长度,l0为 K′系中测量的长度,考虑一与运动方向垂直的长方形面 S,与 K′一起运动,则从 K看 K′中的面 S,面积不变, V=lS构成一封闭的长方体运动空间。从(2)式可得:lS=βl.S,即:

从(3)式可知从相对做匀速运动的不同惯性坐标系中测量一个固定在运动坐标系中的长方体物体的体积时,会发生运动物体体积缩小的相对论效应,体积缩小的倍数即为β。以上讨论中物体的形状是规则的长方体,那么对于任意形状的物体(3)式是否成立?可以证明任意形状物体,静体积V0和动体积V之间仍有关系:V=βV0。

证明:

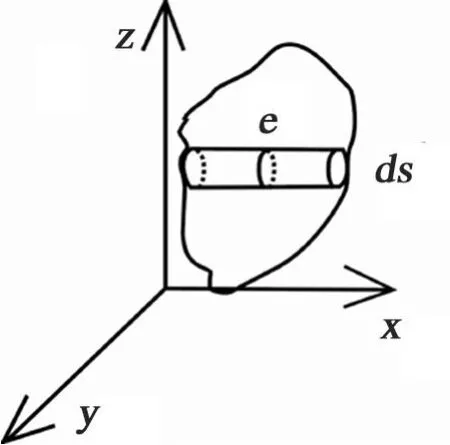
图 1 静体积和动体积的关系示意图Fig.1 Sketch m ap to reveal the relationship betw een static volum e and dynam ic volum e

如图 1,在 K系中,沿运动方向 x取封闭空间中的一微柱体 lds,ds垂直 x轴,则封闭空间的动体积为:

同理在 K′系中,静体积为:

所以有:V=βV0,证毕。

公式(3)是在惯性坐标系中得到的,如果放宽条件让物体以任意速度平动,则静体积和动体积之间仍然有关系 (3)。因为我们可以考察 (dx,dt)内的坐标系,在此瞬间内坐标系可以看成是匀速的,因为是平动,所以 K和 K′之间的长度缩短倍数β在垂直于 x轴的整个平面内是一样的,故仍有关系(3)式。

洛伦兹变换虽然保证了电动力学方程在 K和K′之间变换时形式不变,但牛顿力学对洛伦兹变换是不协变的,为了使牛顿力学方程对洛伦兹变换也协变,我们必须修正牛顿力学的形式[4]。这一修正导致了另外的相对论效应:1)运动物体质量增加;2)质量是一种能量的储存形式,即得爱因斯坦质能方程:E=m c2,本质上质能方程是运动物体质量增加效应的必然结果,设想外界不断地将能量加给物体,使物体运动速度加快,但相对论中光速是所有物体运动的极限速度,所以外界加到物体上的能量,不可能通过速度无限体现,只能通过增加质量无限制地将能量存储到质量中去。

为了使牛顿运动方程对洛伦兹变换协变,同时考虑到相对论时空观中,空间和时间的相关性,闵可夫斯基提出了统一的四维时空概念[5,6],令时间维为:x4=ict,并称四维时空为世界,在四维空间中距离公式和笛卡尔的三维空间中的距离公式形式上完全一样[7]:

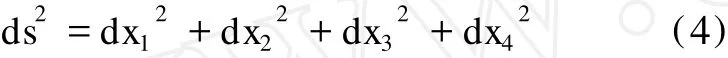
这样洛伦兹变换的必要条件就可表示成:

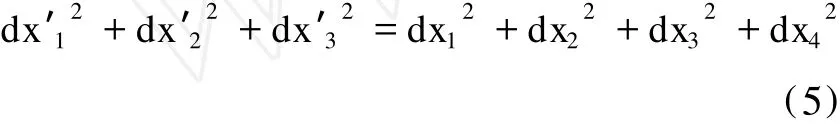
当 ds2=0时,(5)就是光速不变原理,显然洛伦兹变换是必须满足的。

在此基础上将所有的牛顿力学中的三维量改造成四维量,如速度、加速度、动量、力等,并将力学方程改造成张量方程,因为张量方程可以做到对坐标变换是协变的。

经改造后的力学动力学方程为:

其分量方程为:

其中:μ=1,2,3,4。

(7)就是改造后的对洛伦兹变换协变的力学动力学方程,在得到(7)的过程中必须定义新的质量为:

其中m0为静质量,m为动质量。公式 (8)虽然是推理中得到的,但已为粒子加速器实验所证实,(8)表明运动物体的质量会增加。(8)对做平动的变速坐标系在瞬时中也成立。

2 质空积守恒

这一节我们讨论当物体运动时,质量增加和体积缩小之间的数量关系。(3)和 (8)分别给出了在K系和 K′系中度量物体体积和质量的关系公式。

定义:运动物体的体积与它质量的乘积称为运动物体的质空积。

前面我们已经证明了对相对做匀速运动的惯性坐标系和对惯性坐标系做平动的坐标系 (3)和(8)均成立。将 (3)式乘以 (8)式,可得:

(9)式说明,相对于静系静止的物体的质空积等于相对于静系运动的物体的质空积,并且与运动速度无关,即有:

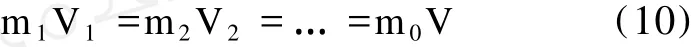
1、2、3…分别表示以不同的速度运动的同一物体,(10)式表明运动的物体的体积与它的质量成反比,体积减小,质量增大。当物体运动速度接近光速时,体积无限小,质量无限大,但乘积保持不变,与速度无关。(10)可写成以下守恒形式。

(11)式表明:质空积守恒。至此我们就得到了运动物体质量和体积之间的数量关系,并证明了:质空积守恒对惯性参照系和平动非惯性参照系成立。

质空积守恒是在狭义相对论中证明的,在广义相对论中 (11)式需在一定假设条件下才能成立。处于引力场中的局域总能找到一个坐标系用惯性力场抵消引力场得到满足狭义相对论的条件,也即质空积守恒成立。但从一个统一的坐标系去考察非均匀的引力场空间中各点时,dm变化引起 dV的变化,dV内的空间能量密度可能不同,所以不能相加,无法积分,故质空积不守恒,但能量守恒仍成立,所以根据宇宙学原理假设:空间能量密度处处相等,并在空间膨胀过程中保持等密度膨胀 (此假设在宇观范围内近似满足)。

将(11)式两边乘以平均的宇观空间能量密度ρ0,得:

E0表示空间中蕴含的能量,(12)式虽然和(11)式是等价的,但 (12)式显式地反映了质量与真空能的关系。

3 质空积守恒与能量守恒的关系

我们考察一个含有物质的有限封闭空间V,其中有质量m,如下图:

我们不去对这个封闭空间做任何改变,仅仅用不同的两个参考系考察它,A参考系相对于封闭空间静止,B参考系以速度 V′运动。封闭空间相对于A参考系的质量为mA,体积VA;相对于B参考系的质量为 mB,体积 VB,根据相对论,mAVB,当从B参照系变到A参照系,质量减少,体积增加,根据爱因斯坦质能公式 E=m c2,质量减少意味着能量减少,由于封闭空间只有体积变化,能量又不可能消失,所以只能是能量转化到增加的空间体积中去了。从这里我们看到空间也是储存能量的一种形式,物质和空间能可以相互转化,所以说质空积守恒本质上是能量守恒的更高级形式。

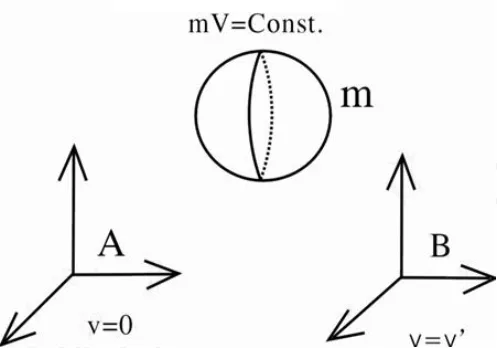
图 2 质量和真空能之间的关系示意图Fig.2 Sketch m ap revealing the relationship betw een m ass and vacuum energy

能量守恒定律的适用范围,在历史上有过多次扩展[8]。人类首先发现动能和势能可以相互转化,遵循机械能守恒定律;后来发现了内能和机械能可以相互转化,遵循热力学第一定律;后来爱因斯坦又发现质量和能量可以相互转化,遵循质 -能守恒定律;这里我们发现质量和真空空间能可以相互转化,遵循质空积守恒,这样将能量守恒定律的适用范围扩展到了包含真空空间能。

以上的推导和分析均属于经典相对论的逻辑范畴,但如果假设 (12)式能定性地适用于整个大爆炸后的宇宙,我们就可以从能量守恒和转化的角度去分析宇宙膨胀问题。从 (12)式看引力质量和蕴含在空间中的暗能量之间可以发生转化,但需遵循能量守恒定律,如果将宇宙膨胀的原因归结为暗能量的斥力引起的,那么宇宙中必存在引力质量不断转化为空间暗能量的机制,即宇宙膨胀是有代价的,可以设想当所有引力质量全部转化为空间能量,并忽略非能量转化引起的宇宙膨胀,则宇宙就不可能再膨胀了。当然(12)式是否真的能定性地适用于整个宇宙需要考证。

在用牛顿力学解决力学问题时,通常有两种方法[9]:1)直接从动力学方程牛顿第二定律出发分析解决问题;2)从能量、动量、角动量等守恒定律出发分析解决问题。在现在的宇宙学中,研究宇宙的膨胀问题,我们一般是用爱因斯坦引力场方程及其解的模型分析解答问题的[10-12],我们还从来没有从能量守恒的角度分析过整个宇宙的膨胀问题,质空积守恒给我们提供了这种可能。

4 总 结

爱因斯坦的质能公式使质量成为储能的一种形式,质空积守恒定律使真空空间也成为储能的一种形式,真空能[13]的增加或减少,必然伴随着其他形式能量的变化。真空空间收缩则质量增加,能量从存储在空间中,转移到存储在质量中;真空空间膨胀则质量减少,能量从存储在质量中转移到存储在空间中,质空积守恒本质上是能量守恒的更高级形式。

[1] 爱因斯坦.爱因斯坦奇迹年[M].范岱年,译.上海:上海科技教育出版社,2001:97-129.

[2] 李醒民.论狭义相对论的创立[M].成都:教育出版社,1994:22-24.

[3] 爱因斯坦.爱因斯坦文集[M].许良英,译.北京:商务印书馆,1976:75-76.

[4] P.G.柏格曼著.相对论引论[M].周奇,译:北京:人民教育出版社,1961:87-107.

[5] 爱因斯坦.相对论原理 (相对论经典论文集)[M].赵志田,译.北京:科学出版社,1980.:61-82.

[6] W.泡利.相对论[M].上海:上海科学技术出版社,1979:95-100.

[7] 爱因斯坦.狭义与广义相对论浅说[M].杨润殷,译.北京:北京大学出版社,2006:96-97.

[8] ErnstM ach.Science of M echanics[M].London:The Open Court Publishing Co.,1942:151-621.

[9] Richard Feynm an.The Feynm an Lectures on Physics V olum e II[M].California:A ddison-W esley Publishing Company, 1964:9-1～14-2.

[10] 爱德华·哈里森.宇宙学[M].李红杰,译.长沙:湖南科学技术出版社,2008:400-402.

[11] 王永久.引力论和宇宙学[M].湖南长沙:湖南师范大学出版社,2004:715-772.

[12] 俞允强.物理宇宙学讲义[M].北京:北京大学出版社,2002:109-112.

[13] 罗恩泽.真空动力学[M].上海:上海科学普及出版社,2003:1-49.

Conversation ofMass2Space Product in Relativity

YIN J ian1,YIN Ye2
(1.D epartm ent of Foundation Courses,W uxi Institute of Technology,W uxi 214121,China; 2.College of Inform ation,M echanical and Electrical Engineering, Shanghai N orm al U niversity,Shanghai 200234,China)

D ifferent reference fram es in Relativity have different space m easurem ent and m ass m easure2 m ent.Cubage of an object decreases and its m ass increases w hen relative object′s rest reference fram e changes into m oving reference fram e.Is there any num erical internal relationship betw een the decrease of cubage and increase of m ass of the object?The paper explored the answ er to this question,and proved that their relationship follow s Conversation of M ass-Space Product,and also proved thatM ass-space Product keeps conservation not only to inertial reference fram e but also to translation non-inertial refer2 ence.B y analyzing the relationship betw een Conservation of M ass-space Product and Conservation of Energy,the paper com es to the conclusion that in object conservation ofM ass-space Product represents the higher level of conservation of energy.

relativity;M ass2space Product;Conversation of M ass2Space Product;W acuum Energy;Con2 versation of Energy

O412

A

1671-7880(2010)04-0052-04

2010-06-05

国家科技支撑计划课题(2007BAK27B02)

殷 建(1963— ),男,江苏无锡人,副教授。