Bézier曲线的光滑拼接

林 芳

(西安建筑科技大学数学系,西安 710055)

Bézier曲线的光滑拼接

林 芳

(西安建筑科技大学数学系,西安 710055)

Bézier曲线是计算机图形学研究的主要内容.曲线的拼接是曲线曲面造型中的关键技术之一.基于 Bézier曲线的拼接原理,在 Visual C++6.0环境下开发 Bézier曲线的拼接程序,将曲线拼接在界面中动态实现.

Bézier曲线 ;拼接 ;连续

1 问题的提出

Bézier曲线是计算机图形学的重要内容.它是描述物体的外型,建立所画对象数学模型的有力工具.Bézier曲线采用分段参数多项式形式,曲线的形状不依赖于坐标系的选取,可直观和简便的人机交互,造型灵活易于控制.但是Bézier曲线不能精确表达除抛物线外的圆锥曲线,为表达复杂曲线在计算机图形学中常用曲线拼接的方法,即将一段段的 Bézier曲线首尾相连拼接起来,以满足实际的需要[1].这里要解决的就是怎样实现光滑连接的问题.

2 Bézier曲线的定义及性质

2.1 Bézier曲线的定义

称为伯恩斯坦基函数.它恰好是二项式[t+(1-t)]n的展开项.曲线采用顶点表示后,给输入与交互修改设计曲线带来莫大的方便,只要移动顶点就可灵活地控制曲线的形状.

2.2 伯恩斯坦基函数的主要性质

(1)非负性:Bj,n(t)≥0;

(4)对称性:Bj,n(t) =Bn-j,n(1-t);

(5)函数递推公式:Bj,n(t) = (1-t)Bj,n-j(t)+tBj-1,n-1(t);

2.3 Bézier曲线的端点性质

(1)Bézier曲线的首末端点正好分别是 Bézier多边形的首末顶点,即 p(0)=b0,p(1)=bn.

(2)Bézier曲线在首末端点的 k阶导矢分别与Bézier多边形的首末 k条边有关,与其他边无关.这表明曲线在首末端点分别与首末条边相切.

其中,Δkbj=Δk-1bj+1-Δk-1bj,Δ0bj=bj,aj为边矢量.

3 参数连续性及几何连续性

光滑连接有两种不同的方式[3]:一种是用函数曲线的可微性,把组合参数曲线构造成在连接处具有直到 n阶连续导矢即 n次连续可微,称为 n阶参数连续性,简记 Cn.组合曲线在连接处满足不同于 Cn的某一组约束条件称之为具有 n阶几何连续性,简记为 Gn[4].

3.1 两种连续性的定义

0阶参数连续性,记作 C0,是指曲线相连.即第一个曲线段在 t=1处的值与第二个曲线段在 t=0处的值相等.一阶连续性记作 C1,指两个相邻曲线段在交点处有相同的一阶导数.二阶连续性记作 C2,指两个曲线段在交点处有相同的一阶和二阶导数.

两段曲线在连接点处首尾相连,它们在连接点达到G0连续.两段曲线在连接点处达到G0连续,且切向相同,它们在连接点处达到G1连续.两段曲线在连接点除达到G1连续外,它们的主法线方向一致且曲率相等,则在连接点达到 G2连续.

3.2 两种连续性的比较

参数连续性与参数选取有关,Bézier曲线在整体参数下的参数连续条件与在局部条件下的连续条件是不相同的,后者只是前者的一种特殊情况.其次,参数连续性实际是用函数曲线的可微性,与函数曲线的光滑度相一致的函数曲线的可微性,当用于参数曲线时,出现了可微性与光滑度不一致的问题.在参数曲线上出现零切矢处虽然仍是可微的,但却可能是不光滑的.反之,光滑的曲线有可能是不可微的.其实,参数连续是对参数曲线连接光滑度的过分限制,是认为强加的限制.参数连续与参数选取及具体的参数化有关,而形状的客观内在几何特征,例如光滑度是不依赖于参数选取与具体参数化的.正是由于参数连续性不能客观准确度量参数曲线连接的光滑度,取而代之的就是几何连续性[5].

几何连续性与参数选取及具体的参数化无关,这就排除了由参数选取引起的非正则情况.组合曲线在连接处的光滑度或光顺性与组合曲线整体的光顺性是不矛盾的,前者包含在后者之中.通过上面的关于几何连续性的介绍,两条 Bézier曲线拼接到一块可以达到最高 G2连续性,最低 G0连续性[6].在本文中通过Visual C++在界面中将 G0,G1,G2连续实现.

4 程序实现

Bézier曲线的生成用伯恩斯坦基函数表达通过 Visual C++编程实现.图 1所示,是两条 Bézier曲线,一条是二次的,一条是三次的,这是两条未拼接之前的曲线形状.

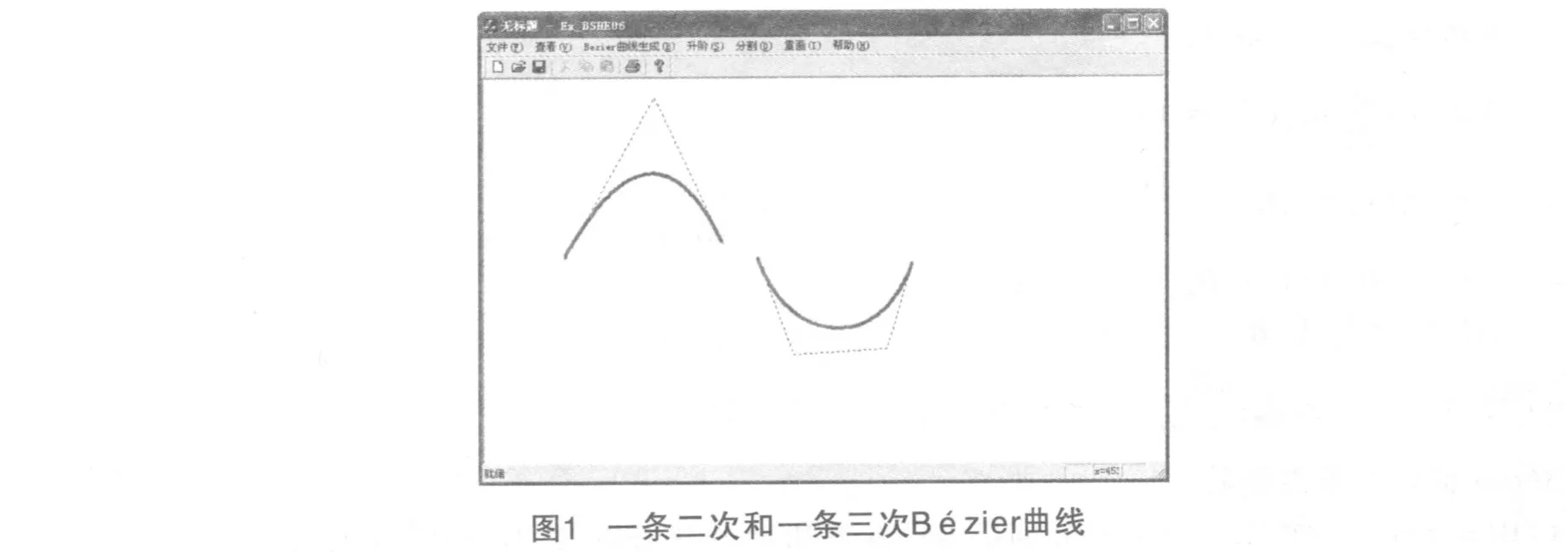
图2和图 3展示了这两条Bézier曲线的拼接过程,仅移动右下方曲线的左上顶点.从图 3可以看出,这时连接成一条复杂曲线,但是在连接点处关于弧长的一阶导矢不是相同的,只是达到了 G0连续性.

移动图 3中的B点,使AB的斜率与左上的二次曲线的第二条控制边的斜率相同,得到如图 4的效果.这时在连接点处实现了有公共的切矢,从而使曲线在连接处达到了 G1连续性.

如果继续移动图 4中的 C和D点,移到如图 5的位置,那么我们可以发现在A点处两条曲线有公共的曲率矢,从而实现了二阶几何连续,即 G2连续性.

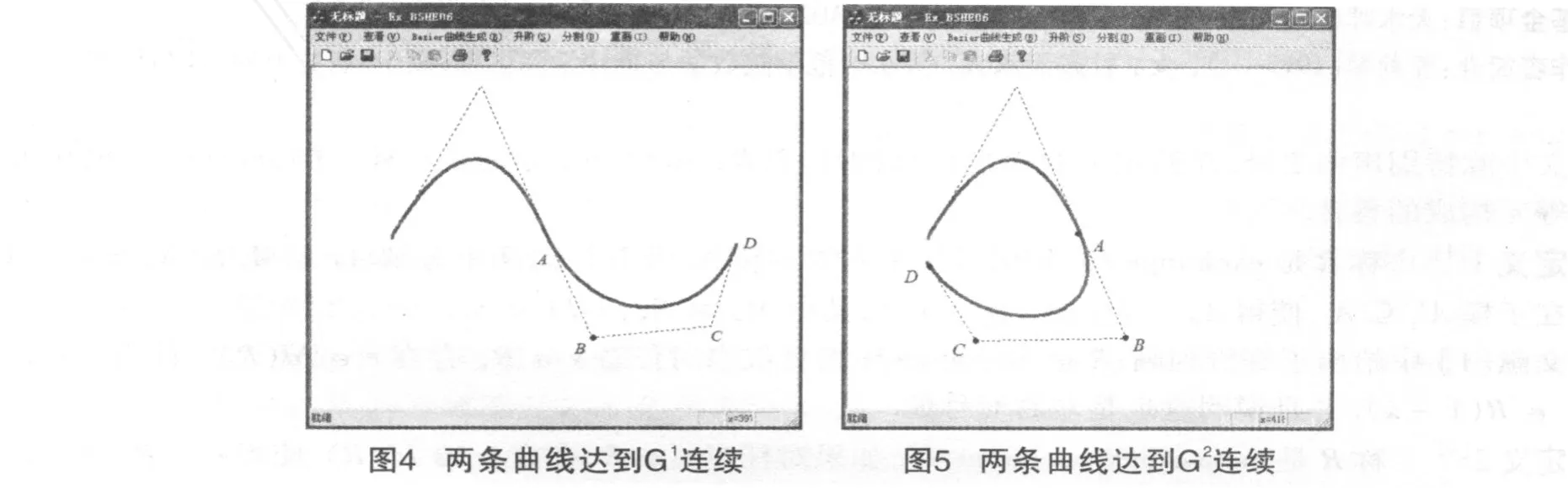
这样,完成了两条Bézier曲线在满足不同连接条件的拼接.同时我们拼接成的曲线有较好的局部控制性.

5 结论

在实际应用中,对于难以用单一的一段曲线描述的复杂曲线,可以通过曲线的拼接来实现.从上图中可以看出曲线拼接满足 G2连续,具有光滑度,有其显著的应用价值.同时,曲线的拼接思想可以推广到曲面的拼接,对算法进行修正即可.

[1]芦殿军.Bézier曲线的拼接及其连续[J].青海大学学报 (自然科学版),2004,22(6):84-86.

[2]施法中.计算机辅助几何设计与非均匀有理 B样条[M].北京:高等教育出版社,2001.

[3]Donald Hearn,M.Pauline Baker.Computer Graphics[M].American:Addison-Wesley,1998.

[4]严兰兰,宋来忠,李军成.有理 Bézier曲线的拼接[J].三峡大学学报 (自然科学版),2005,27(5):469-471.

[5]唐荣锡,汪嘉业,彭群生.计算机图形学教程[M].北京:科学出版社,1990.

[6]陈宝平,赵俊岚,尹志凌.有理参数曲线的光滑拼接[J].内蒙古大学学报 (自然科学版),2008,39(3):357-360.

[责任编辑 舒尚奇]

The Smooth Connection of Bézier Curve

L IN Fang
(Depar tment of Mathematics,Xi’an University ofArchitecture and Technology,Xi’an 710055,China)

Bézier Curve is one of the most elementary contents in the computer graphics.The connection ofBézier Curve is one of the most elementary technologies in the computer graphics.Based on the principle about the connection ofBézier Curve,the connection ofBézier Curve can be dynamically realized in the menu interface byVisual C++6.0.

Bézier Curve;connection;continuity

TP391

A

1009—5128(2010)05—0003—03

2010—06—10

西安建筑科技大学青年基金 (QN0933)

林芳 (1971—),女,上海人,西安建筑科技大学副教授,硕士.研究方向:计算机图形及辅助制造.