关于Meta-sided Exchange环的几点注记

郭莉琴,何建伟,卲海琴

(天水师范学院数学与统计学院,甘肃天水 741001)

关于Meta-sided Exchange环的几点注记

郭莉琴,何建伟,卲海琴

(天水师范学院数学与统计学院,甘肃天水 741001)

给出了 meta-sided exchange环的性质;讨论了Morita系统环的 meta-sided exchange性质和具有零化条件的 meta-sided exchange环;证明了满足一定条件的 meta-sided exchange环是环.

exchange环;meta-sided exchange环;Morita系统环;环

文中除特别声明之外,总假定 R是有单位元的环.J(R)和 Id(R)分别表示环 R的 Jacoboson根和由 R的幂等元构成的集合.

定义 1[1]称 R是 exchange环,如果对每个右 R-模AR及其任意两个分解 AR=MR⊕ NR=⊕i∈IAi,都存在子模 A′i⊆ Ai,使得 AR=MR⊕ (⊕i∈IA′i),其中 MR≅ RR,|I|< ∞.

文献[1]中给出了等价刻画:R是 exchange环当且仅当对任意 x∈R,存在 e∈Id(R),使得 e∈Rx,1-e∈R(1-x).并且说明这也是左右对称的.

定义 2[1]称 R是 meta-sided exchange环,如果对任意 x∈R,存在,e∈Id(R)使得 e∈Rx,1-e∈R(1-x)R,.meta-sided exchange环并没有上述的对称结构.

从以上的两个定义可以看出,meta-sided exchange环是 exchange环的推广.由meta-sided exchange环的定义易得:

引理 1 meta-sided exchange环的同态像是 meta-sided exchange环.

命题 1 如果 R是 meta-sided exchange环,e∈ Id(R),则 eRe和 (1-e)R(1-e)是 meta-sided exchange环.

证明 设任意 x∈eRe,由 R是 meta-sided exchange环,存在 f∈Id(R),使得 f∈Rx,1-f∈ (1-x)R.则 fe=f,(ef)2=ef∈ (eRe)x,e-ef=e(1-f)e∈ (e-x)eRe.

故 eRe是 meta-sided exchange环.类似地,可证 (1-e)R(1-e)是 meta-sided exchange环.

下面讨论Morita系统环的 meta-sided exchange性质.

设 (A,B,M,N,ψ,φ)表示 Morita系统环,其中 A和 B都是环,BMA和ANB都是双模,ψ:N ⊗M →A,φ:M ⊗N →B是双模同态,且满足:ψ(ν⊗w)ν′=ν φ(w ⊗ν′),φ (w ⊗ν)w′=wψ(ν⊗w′),这些条件保证了关于普通矩阵的加法和如下定义的下乘法:作成环,称为Morita系统环.[2]

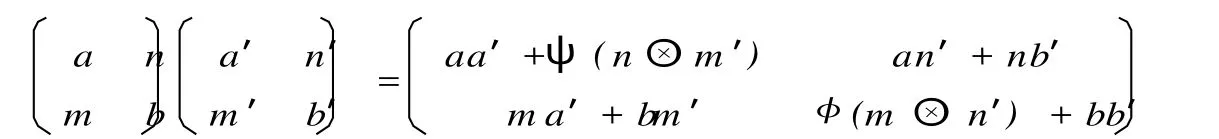
证明 (必要性)定理 1中已证.

(充分性 )设 T是 meta-sided exchange环,令因为

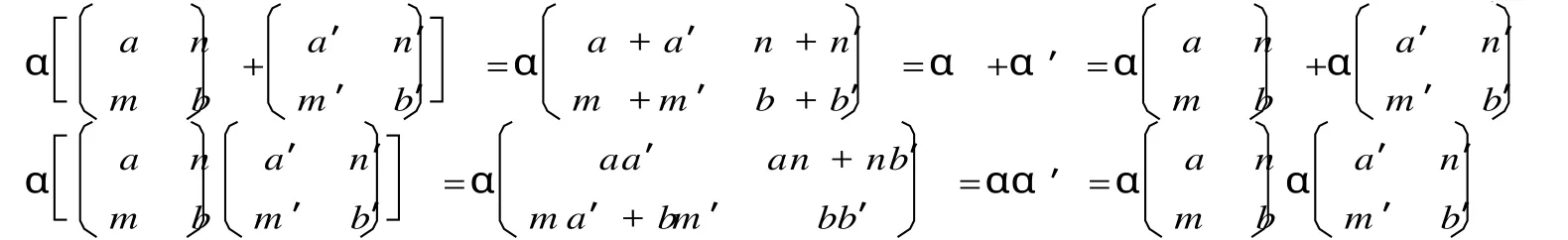
所以α是环同态,显然α是满的.同样可验证β也是满的环同态,因此A和B都是 T的同态像,由引理1知 A和 B都是 meta-sided exchange环.

下面讨论具有零化条件的meta-sided exchange环.l(a)和 r(a)分别表示元素 a的左零化子和右零化子.

引理 2 设 R是meta-sided exchange环,则对任意 a∈R,存在幂等元 e∈R,使得 a的右零化子 r(a)⊆eR,l(1-a)⊆R(1-e).

命题2 设R的每个主左理想是左零化子且每个主右理想是右零化子,则R是meta-sided exchange环当且仅当对任意 a∈R,存在幂等元 e∈R,使得 r(a)⊆ eR,l(1-a)⊆ R(1-e).

定义 3[4]称 R是 I-环,如果 R的每个非诣零的右理想都包含非零幂等元.

定理 3 设 R是环,对 R的任意非零右理想 I,都满足条件 I∩C(R)≠0.如果 C(R)是半本原的meta-sided exchange环,则 R是 I-环.

证明 反设 R不是 I-环.则存在 R的非诣零的右理想 I,它不包含非零幂等元.而 I∩C(R)≠0,则存在 0≠a∈I∩C(R).因为 C(R)是meta-sided exchange环,所以存在幂等元 e∈R,使得 e∈C(R)a,1-e∈ (1-a)C(R).由假设和 C(R)a⊆ I知,e只能是 0,则有 1=1-e∈ (1-a)C(R),因此 1-a是右可逆的.对任意 s∈C(R),同理可知,1-as是右可逆的.由[5,定理 15.3]知,a∈J(C(R)),则J(C(R))≠0,这与 C(R)是半本原的矛盾.故 R是 I-环.

[1]CHEN huan-yin.On one-sided exchange rings[J].Journal of Mathematics study,1998,31(2):145-148.

[2]HughanyA.Hopficity and co-hopficity forMorita contexts[J].Comm Algebra,1999,27(1):477-492.

[3]A.haghany,K.Varadarajan.Study of formal triangularmatrix rings[J].comm.Algebra,1999,27(11):5507-5525.

[4]C.Y.Hong,N.K.Kim,Y.Lee.Exchange rings and their extensions[J].J.Pure Appl.Algebra,2003,179(9):117-126.

[5]F.W.Ander son,K.R.Fuller.Rings and Categories ofModules[M].New York:Springer-verlag,1992:166-170.

[6]Pace P.Nielsen.Square-free moduleswith the exchange property[J].J.Algebra,2010,323(12):1993-2001.

[7]薛利敏,舒尚奇.利用行列式性质求矩阵的特征值[J].渭南师范学院学报,2010,25(2):13-17.

[责任编辑 舒尚奇]

Some Notes for Meta-sided Exchange Rings

GUO Li-qin,HE Jian-wei,SHAO Hai-qin
(School of Mathematics and Statistics,TianshuiNormalUniversity,Tianshui 741001,China)

Some properties ofmeta-sided exchange are given.The properties of meta-sided exchange aboutMorita contexts are investigated.And meta-sided exchange with certain annihilator condition is considered.It also proved thatmeta-sided exchange ring is I-ring under some additional conditions.

exchange ring;meta-sided exchange ring;Morita contexts ring;ring

O153.3

A

1009—5128(2010)05—0006—02

2010—05—31

天水师范学院中青年教师科研资助项目 (TSA020231)

郭莉琴 (1977—),女,甘肃天水人,天水师范学院数学与统计学院讲师,硕士.研究方向:环与代数.