n阶行列式计算方法探讨

唐仙芝，刘春新

（黄河水利职业技术学院，河南 开封 475003）

n阶行列式计算方法探讨

唐仙芝，刘春新

（黄河水利职业技术学院，河南 开封 475003）

行列式计算的技巧性很强．文章探讨了行列式的几种特殊计算方法，涉及范得蒙行列式、数学归纳法、拉普拉斯定理、方阵特征值与行列式的关系等内容．

行列式；拉普拉斯定理；范得蒙行列式

n阶行列式的计算是线性代数中的一个重要问题，也是一个很复杂的问题，其技巧性很强．理论上任何一个n阶行列式都可以按定义计算，但是当n较大时，直接按定义计算而不借助于计算机几乎是不可能的．因此，探寻n阶行列式的计算方法是十分必要的．本文给出n阶行列式的几种特殊计算方法，它们基本上可以解决一般的n阶行列式的计算问题．

1 利用范得蒙行列式进行计算

例1[1]计算行列式Dn+1，其中

分析：该行列式与范得蒙行列式很相似，可以先利用行列式的性质把它变为范得蒙行列式再进行计算．通过相邻两行的交换，先把最后一行交换至第一行（交换n次），再将新的最后一行交换至第二行（交换n−1次），如此继续下去，经过n(n + 1)/2次交换后，原行列式变为范得蒙行列式．

解：由范得蒙行列式的性质得

2 利用数学归纳法进行计算

数学归纳法多用于证明题．用数学归纳法计算 n阶行列式，需要对同结构的低阶行列式进行计算，从中发现规律并得出一般性结论，然后再用归纳法证明其正确性．

例2[2]计算行列式Dn+1，其中

3 利用拉普拉斯定理进行计算

拉普拉斯定理是行列式按一行或一列展开定理的推广．在应用拉普拉斯定理时，为了计算上的方便，一般先利用行列式的性质对原行列式进行变形，再按含零多的k行或k列展开．

例3 计算行列式Dn，其中

分析：如果从第3行开始每一行都减去第2行，再从第3列开始每一列都加到第2列，可使行列式中更多的元素为零．

解：先按上述分析对行列式进行变换，

再由拉普拉斯定理可得

4 利用方阵特征值与行列式的关系进行计算

例4 计算行列式Dn，其中

显然bEn的n个特征值为b，b，…，b，而An的n个特征值为故A的特征值为

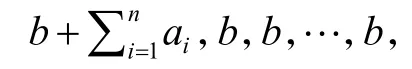
由方阵特征值与对应行列式的关系知

5 利用特殊公式进行计算[3]

设α，β 是方程 x2− ax + bc=0的两个根，则

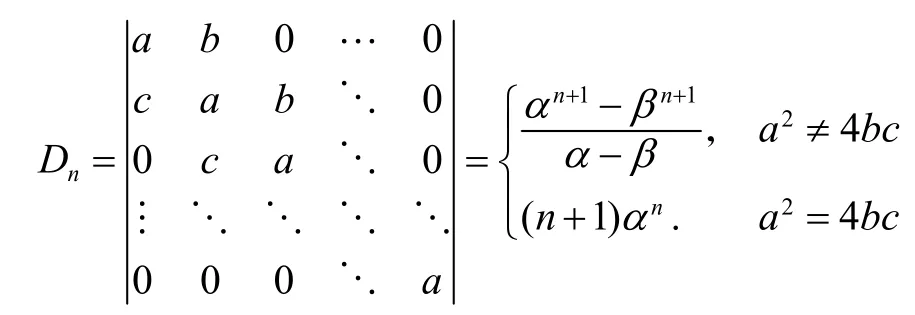
我们先证明这个特殊公式：将Dn按第1行展开，再将展开式中的第2个行列式按第1行展开，可得

令 α+ β=a，α β=bc，即α，β 是方程 x2− ax + bc=0的两个根，则

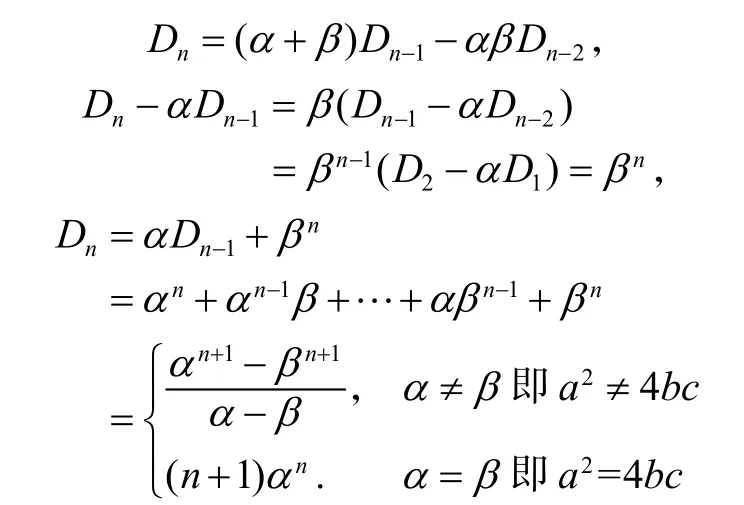
例5[1]计算行列式Dn，其中

6 通过构造新行列式进行计算

例6[4]计算行列式Dn，其中i≠j时ija≠a，

解：在Dn中加1行1列可配成范得蒙行列式，即

由于Dn是多项式 Dn+1(y)中 yn−1的系数的相反数，所以

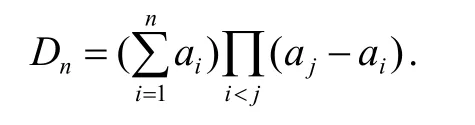
例7[5]若a≠b，计算行列式

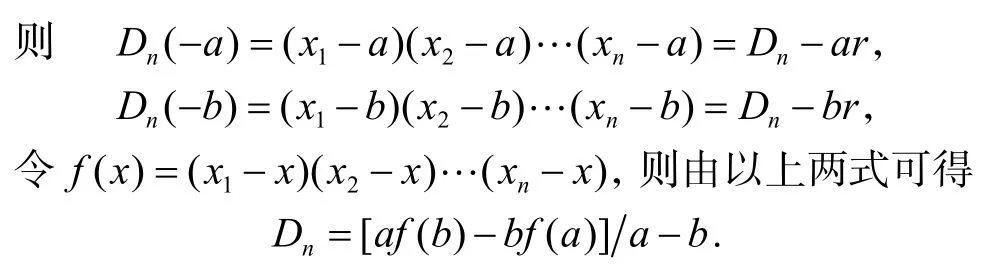
解：构造新行列式例8[5]计算循环行列式

由上述3例可见，为简化行列式的计算，有时需要先根据题设条件构造一个新行列式．

[1] 王品超．高等代数新方法：下册[M]．徐州：中国矿业出版社，2003．

[2] 北京大学数学系几何与代数教研室代数小组．高等代数[M]．2版．北京：高等教育出版社，1998．

[3] 徐甫华．线性代数典型题精讲[M]．大连：大连理工大学出版社，2002．

[4] 钱吉林．高等代数题解精粹[M]．北京：中央民族大学出版社，2002．

[5] 徐仲．线性代数典型题解集[M]．2版．西安：西北工业大学出版社，2000．

〔责任编辑 张继金〕

Calculation of n-order Determinant

TANG Xian-zhi,LIU Chun-xin
(Yellow River Conservancy Technical Institute,Kaifeng Henan 475001,China)

The determinant calculation relies much more on techniques. Some special methods of calculating the determinant are discussed,which relates the relationship between determinant and Van De Monte,mathematical induction,Laplace theorem as well as matrix eigenvalue. the of the content

determinant; Laplace theorem; Van De Monte determinant

O151.2

A

1006-5261(2010)05-0004-03

2010-03-25

唐仙芝（1967―），女，河南开封人，副教授．