关于优化数学分析课程教学质量的思考
张秀全,彭 真
(黄淮学院 数学系,河南 驻马店 463000)
关于优化数学分析课程教学质量的思考
张秀全,彭 真
(黄淮学院 数学系,河南 驻马店 463000)
在数学分析课程的教学中,要重视概念的引入,以增强课堂教学的趣味性;要重视概念之间的联系,以帮助学生掌握理论的精髓;要重视形象化教学,以帮助学生理解抽象的概念;可采用多媒体辅助教学,以创造生动活泼的教学氛围.
优化;数学分析教学;学科交叉;课程体系整合
数学分析是数学专业重要的主干基础课之一,是分析数学系列课程的中心,是近现代数学理论教育的重要基础.数学分析不仅为学生学习后续课程提供必要的基础,而且它所体现的分析数学思想、逻辑推理方法、处理问题的技巧,对整个数学学习和科学研究起着奠基作用.数学分析课程有助于锻炼和提高学生的理性思维能力、数学表达能力、综合应用能力与科学创新能力,对学生数学基本素质的培养起着十分重要的作用.许多教师都讲授过数学分析课,但真正能把它讲好且能实现教学目标的不多.目前,数学分析课程的教学质量不容乐观.笔者认为,提高数学分析课程教学效果的关键是提高学生的学习兴趣,激发学生的学习动力.
1 重视概念的引入,增强课堂教学的趣味性
数学分析的基本思想蕴涵于有着千丝万缕联系的基本理论、概念、定理、性质、法则、公式之中,因此,概念教学是数学分析教学的基础.
概念是一种思维形式,又是思维的基本结构单位,一切分析、想象、推理都要依据概念和运用概念.在教学中,学生只有透彻理解教学概念,才能灵活掌握运算的技能和技巧.概念教学有助于培养学生分析研究问题和解决问题的能力.为抓好概念教学,教师要剖析每个概念的本质,并增强概念教学的趣味性.
(1)教师在教学过程中,教师要重视概念的引入.初学一个数学概念时,学生从具体的实例或教学模型中首先得到概念的直觉认识,然后经过分析、综合,从特殊到一般,从具体到抽象的思维过程,逐步理解有关概念中的本质属性和数学语言.对此,只要教师讲解时概念引入得力,学生就会将生活中已知的现象,通过加工提炼和高度概括,使直观认识得以升华,初步掌握数学概念.概念引入要有趣味性,但也不能缺乏科学性,这样才会使学生越学越深入.
(2)要注意概念的深化.在数学概念引入之后,学生对概念的掌握仍只处于初级阶段,尚不能用概念去分析和解决问题.学生往往由于对概念的理解还存在片面性,不能全面分析问题,容易引起概念判断上的失误;或因对概念缺乏实质性的认识,致使思维活动受限,难以打开逻辑判断通道.这是学生学习数学概念时都会经历的一个阶段,因此教师必须对学生不断地进行深化概念训练,具体训练方法可根据内容特点而定.例如,教师要通过各种典型问题,从各种不同角度让学生深入理解概念,让学生发现自己片面性理解的误区,从而对概念有完整、全面的理解,并逐步形成自己的观点.
2 重视概念之间的联系,帮助学生掌握理论的精髓
数学分析课程抽象性强,学习难度大,学生容易因为学不会而丧失学习兴趣和信心.因此,教师要教给学生学习的方法,设法帮助学生掌握理论的精髓.数学分析课程的系统性很强,将相关的概念联系起来学习,便于学生系统地掌握理论的精髓.
例如,微分学中的罗尔定理、拉格朗日定理、柯西中值定理等是微分学的基本定理,如果教师只是孤立地讲授这些定理,学生很难掌握定理的精髓.为了便于学生系统地掌握这些定理,教师可引导学生建立这些定理之间的联系,即:

再如,不定积分与定积分是两个不同的概念,但是它们之间存在着一定的联系.这种联系是由著名科学家牛顿和莱布尼茨发现的,所以就有了牛顿–莱布尼茨公式:
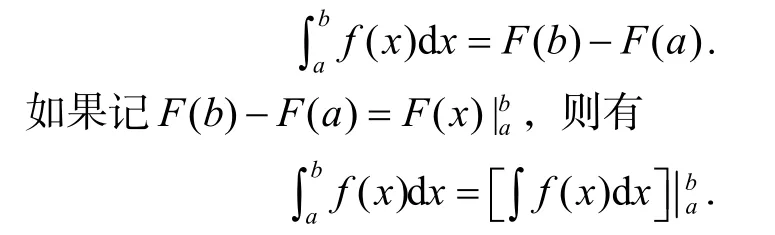
又如,定积分、重积分、线积分、面积分等都是从不同的具体原形抽象概括出来的,但它们之间却有着本质的联系,它们的思想方法都是“分割取近似,求和取极限”.
3 重视形象化教学,帮助学生理解抽象的概念
在数学分析课程教学中,教师可以采取形象化教学方法,变抽象为直观,帮助学生理解抽象的概念.例如,对于正项级数的比较检验,有如下命题:设u1+u2+…和 v1+v2+…都是正项级数,如果存在正整数N,对一切n > N都有vn≥un,则 v1+v2+…收敛时u1+u2+…也收敛,u1+u2+…发散时 v1+v2+…也发散.此结论可理解为“如果较大的级数收敛,那么较小的级数也收敛;如果较小的级数发散,那么较大的级数也跟着发散”.为了让学生接受这个结论,笔者设计了一个“吹气球”实例:把无穷级数的各项相加过程看作吹气球,即每向气球吹一次空气,相当于无穷级数加上一项,气球爆炸相当于级数发散,一直吹气气球总不爆炸相当于级数收敛到一个有限的数;假设有两个相同的气球u和v,第n次向这两个气球充入空气的体积分别为un和vn,n=0,1,2,…,若vn≥un,则一直吹气时,只要气球u爆炸,气球v必定爆炸.这一实例可直观地解释“n≥1时,如果 vn≥un,则v1+v2+…收敛时,u1+u2+…一定收敛;u1+u2+…发散时,v1+v2+…一定发散”,再考虑 u1+ u2+…+ uN和v1+ v2+…+ vN都是有限数,这样学生就能很好地理解所分析的命题.
4 采用多媒体辅助教学,创造生动活泼的教学氛围
根据教学内容,在使用粉笔与黑板进行数学分析课程教学的同时,可适当地结合多媒体技术进行教学.多媒体教学可以充分利用图像、声音、动态等媒体,创造出更为生动活泼的教学氛围,从而调动学生学习的积极性,增加学生学习的兴趣.例如,动态几何软件可以动态地演示函数的变化规律,教师在课上只需要点击事先设置好的图标,就可以将以前需要许多课时讲解才能描述清楚的内容,通过形象生动的动态图形演示变得一清二楚,而且也节省大量的课时.多媒体教学不仅能使枯燥的说教变成形象生动的动态展示和讲解,增强教学内容的直观性、形象性、化难为易、化抽象为具体,由浅入深地进行教学,而且还能让学生在教师的引导下通过自己的研究、观察,将实践上升到理论高度.在数学分析课程教学中,适当地进行多媒体教学能极大地发挥学生学习的主观能动性,激发学生的学习热情,激发学生再发现的欲望,有利于学生的自主学习,有利于提高教师的教学效率.因此,在数学分析课堂教学中,根据教学内容,适度地选择多媒体进行教学,加强数学分析课程与现代化教育技术的有机结合,可以取得较好的授课效果.
[1] 华东师范大学数学系.数学分析[M].3版.北京:高等教育出版社,2001.
[2] 周科,钟智.《数学分析》课多媒体教学初探[J].广西师范大学学报,2000,17(1):58―60.
[3] 王昆扬.关于 Riemann积分理论的本质缺陷及以Lebesgue积分取代之的看法[J].数学教育学报,1999,8(3):95―98.
[4] 张永锋.高师数学分析教学的研究与实践[J].咸阳师范学院学报,2009,24(2):93―94.
〔责任编辑 牛建兵〕
G420
A
1006-5261(2010)05-0071-02
2009-10-10
黄淮学院教学与改革研究项目(2008004)
张秀全(1974―),男,河南驻马店人,讲师,硕士.

