非线性弯曲波摄动后的混沌行为

张善元,刘志芳,张 涛

(太原理工大学应用力学与生物医学工程研究所,太原030024)

比较式(20)和(21),则有

相应的Melnikov函数为

其中 f∧g=f 1 g2-f 2g1.由于g1=0,上式变成

其中

其中

从20世纪60年代起,孤子和混沌在许多领域得到了广泛的研究和应用。从数学上来看,两者都是非线性的产物,然而孤子和混沌分处完全可积分和不可积分系统的两个极端,它们的运动形态呈现出截然不同的行为。孤子解是一种稳定的行波解,两孤子间的作用表现出犹如粒子碰撞一样的守恒性质;而混沌解却对初始条件表现出极度的敏感性,以至系统的长期行为不可预测。一般孤子解是在Hamilton系统讨论的,如果该系统受到摄动(如阻尼、外力等的作用),运动将如何演化?这是一个很自然的问题。另外,在这两类问题的定性分析中,在一定条件下都可能出现同宿或异宿轨道。在非线性波的问题中,同宿轨道对应着孤立波,异宿轨道对应着冲击波;而在混沌研究中,同(异)宿轨道的破裂将是通向混沌运动的一个途径。由此可以得到启示,两类貌似截然不同的非线性运动现象,将有可能在某些方面有所联系,这正是本文工作的一个基本出发点。

同流体力学、等离子物理现象以及光学领域相比,对固体结构中非线性波的研究工作相对要少得多,而且集中于一维非线性纵波的研究。最近,作者讨论了有限挠度梁中非线性弯曲波的传播特性[1-3],得到了精确的周期波解及孤立波解。一个实际的梁结构,或多或少会有阻尼耗散,同时常常受到外加载荷的激励。容易想到,阻尼和外加载荷的引入,会导致同(异)宿轨道的破坏,甚至到一定程度有可能出现横截同(异)宿点。本文在讨论有限挠度梁中非线性弯曲波传播特性的基础上[1],引入外加载荷和阻尼对系统的摄动,利用Melnikov函数[4-6],给出了横截同(异)宿点出现的阈值条件,从而表明系统具有Smale马蹄意义下的混沌性质。为了得到Melnikov函数的一个明确表达式以揭示孤立波(冲击波)进入混沌运动的机制,我们取外部激励为

的特殊形式[7],这并不改变问题的固有性质。

1 Timoshenko梁的运动方程及简化

Timoshenko梁理论认为梁的挠度w由两部分组成,即

其中,w b和w s分别是由弯曲变形和剪切变形产生的挠度。式(1)对 x求偏导,则有

轴向平衡

横向平衡

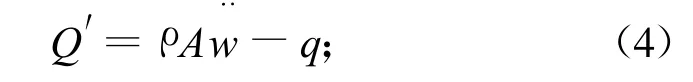
转动平衡

式中,M,Q,N分别为梁截面上的弯矩、剪力和轴力;u和w分别为梁中面上任意点的轴向和横向位移;(′)表示对x求偏导;(◦)表示对时间 t求偏导。在得到以上方程时认为梁是保守系统,没有考虑阻尼力的作用。在实际问题中,阻尼是不可避免的,然而准确地考虑阻尼作用是一件复杂的事情,这里假定阻尼力与横向运动速度成正比,即在(4)式右端增加一项v w◦,其中v是阻尼系数。梁的几何方程除(2)以外,尚包括梁的曲率—挠度关系

以及梁的中面伸长—位移关系

梁的本构关系假定为线性,则

式中,μ是与截面形状有关的因子(μ＜1)。将本构关系(8)、(9)、(10)和几何方程(6)、(7)代入到平衡方程中,不难得到支配 Timoshenko梁中弯曲波的非线性偏微分方程组

采用行波法求解,假定

其中,k和c为常数,k为波数,c为波速。参照文献[1]的步骤,完成积分,消去u和 Ψ,可将偏微分方程组(11)转化为一个φ关于ξ的常微分方程：2

其中

若不计外加载荷与阻尼的作用,得到式(12)的派生方程

文献[1]中的定性分析表明,式(14)在相平面上存在异宿轨道,它对应着冲击波解。进而利用齐次平衡原理和Jacobi椭圆函数展开,给出了式(14)的冲击波解

2 Melnikov函数求解

为分析非线性弯曲波摄动后的混沌行为,现讨论具有外加载荷和阻尼项的方程(12)。根据文献[1],当m→1时,k2→δT1/2,式(12)可以改写为

其中,ε为一小参数,式(16)最终可以写成

比较式(20)和(21),则有

相应的Melnikov函数为

其中 f∧g=f 1 g2-f 2g1.由于g1=0,上式变成

将式(15)带入到式(24),其中式(15)右边取负号,则有

式(25)中第一项积分利用留数定理可以得到,第二项积分由于被积函数为奇函数而得零。于是有

第三、四项积分经简单运算可得：

将I 1,I2,I3和I4代入到式(25)得：

由式(17),有

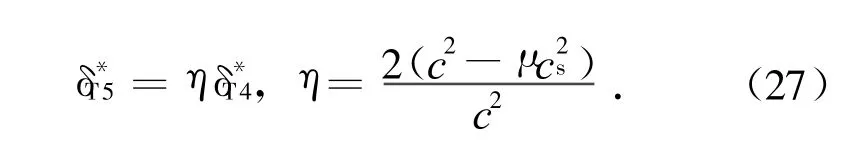
从而式(26)变成

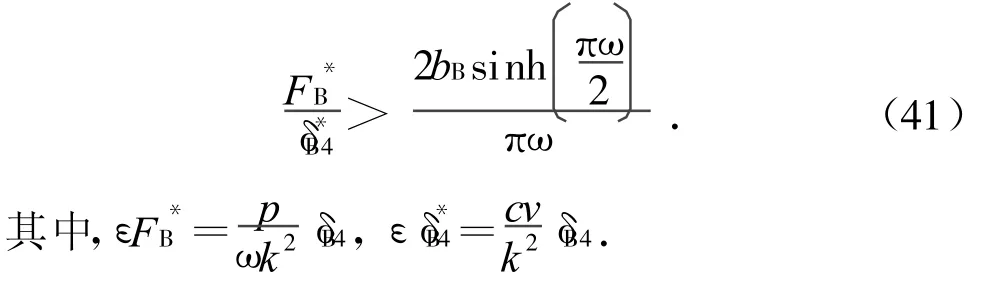
根据Melnikov准则,当

时,M(θ)有简单零点,由此表明系统在一定条件下会出现Smale马蹄意义下的混沌。

3 Rayleigh修正梁

对于Rayleigh修正的梁理论,不计剪切变形,即φ-Ψ=0,此时Q只能参加力的平衡,而不能作为广义内力。于是式(12)简化为由两个方程组成的非线性偏微分方程组

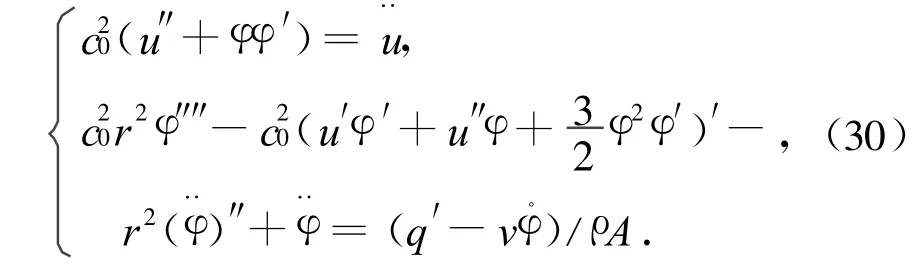
采用行波法求解,参照文献[1]的步骤,可将偏微分方程组(30)化为φ关于ξ的常微分方程

其中

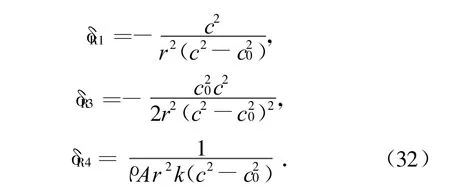
如果略去外部激励和阻尼的影响,则得到式(31)的派生方程为

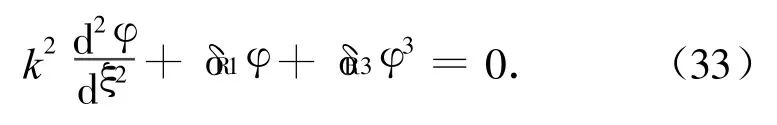
在文献[1]中,通过对式(33)定性分析,表明系统在相平面上存在同宿轨道,它对应着孤立波解,通过Jacobi椭圆余弦函数展开给出了式(33)的孤立波解：

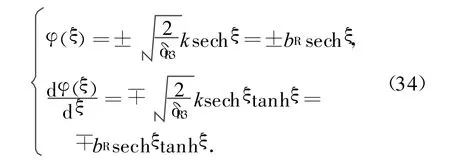
仿照第3节的讨论步骤,不难完成外加载荷和阻尼对同宿轨道的摄动分析。由Melnikov函数同样可以得到系统(31)出现Smale马蹄意义下的混沌的阈值条件：

其中

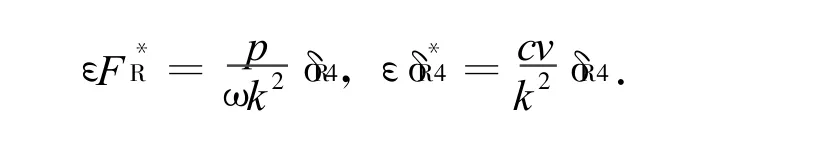
4 Bernoulli-Euler梁

对于经典的Bernoulli-Euler梁理论,不计剪切变形和转动惯性的影响,其支配方程只需略去方程(30)中的r2″项便可得：

采用行波解法求解,完成必要的积分,偏微分方程组(36)最终可化为

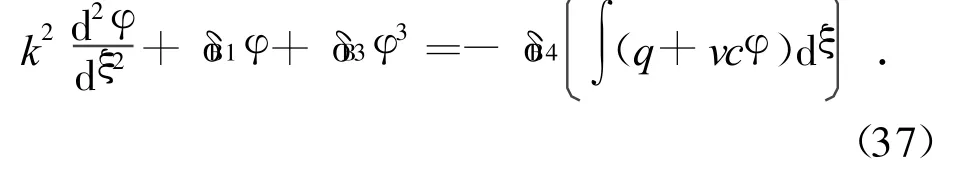
其中

若略去外部激励和阻尼的作用,则式(37)简化为如下自治系统

在文献[1]中,已经证得该自治系统在相平面上存在异宿轨道,它对应着冲击波解。进一步采用Jacobi椭圆正弦函数展开,得到了式(39)的冲击波解：

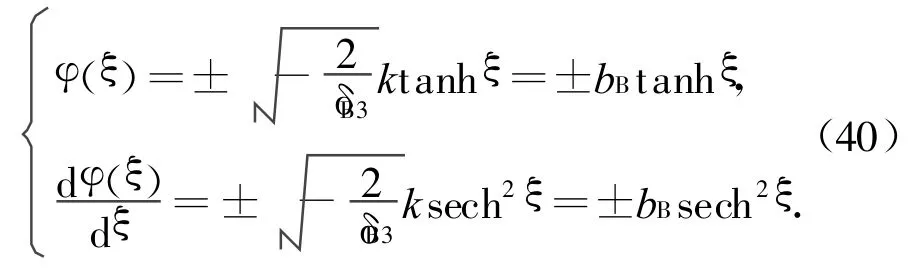
利用Melnikov函数和解(40),可得系统(37)出现Smale马蹄意义下的混沌的阈值条件：

5 结果与讨论

1)作者在文献[1]中研究了无限长Timoshenko梁、Rayleigh修正梁和 Bernoulli-Euler梁中非线性弯曲波的传播,结果表明,在一定条件下会形成孤立波或冲击波。本文在此基础上,引入外加载荷和阻尼对同(异)宿轨道的摄动,利用Melnikov方法给出了横截同(异)宿点出现的阈值条件,表明在一定条件下系统可能出现Smale马蹄意义下的混沌,从而揭示了孤波与混沌两大类非线性现象之间内在的本质联系。

2)在对时域混沌问题研究时,利用Melnikov方法得到混沌条件后,通常还要选择某些特定参数计算相轨迹图、时程曲线和poincaré映射,可以给出混沌运动的具体信息。本文不关心混沌运动的具体细节,所以没有进行更多的数值计算,而重点是在揭示两类非线性现象之间的关联。

3)梁是固体结构中最常用的结构元件之一,关于梁中非线性弯曲波的研究无论是在学术上还是在应用上都有重要意义。目前尚未看到他人在这方面的工作。本文利用文献[1]得到的冲击波解和孤立波解,引入了阻尼和外加载荷对系统的摄动作用,显然这种引入在物理上是很自然的,在实践中是合理的。

[1] 张涛,刘志芳,张善元.三类有限挠度梁中的非线性弯曲波[J].太原理工大学学报,2009,40(4)：440-445.

[2] Zhang Shanyuan,Liu Zhifang.Three kinds of nonlinear dispersive waves in finite deformation elastic rods[J].Ap pl Math M ech,2008,29(7)：909-917.

[3] Zhang Shanyuan,Liu Zhifang,Lu Guoyun.Nonlinear flexural waves in large-deflection beams[J].Acta Mechanica Solida sinica,2009,22(4)：287-294.

[4] 刘曾荣.混沌的微扰判据[M].上海：上海科技出版社,1994.

[5] Nayfeh A H,Balachand ran B.Ap plied Nonlinear Dynamics[M].New York：John Wiley and Sons,1995.

[6] M elnikov V K.On the stability of the center for time periodic peturbations[J].Trans Moscow Math Soc,1963,12：1-57.

[7] Blyuss K B.Chaotic behavior of the solutions to a perturbed Korteweg-de Vries equation[J].Reports on Mathematical Physics,2002,49：29-38.