基于改进遗传算法的煤矿探测机器人路径规划

周 巍,李元宗

(太原理工大学机械工程学院,太原030024)

我国是煤炭资源大国,也是世界上最大的煤炭生产国和消费国。然而,由于矿井自然条件差,高瓦斯矿井多,随着近年来国家对煤炭资源需求量的不断增长,使得煤矿开采中瓦斯爆炸、涌水、着火等事故频繁发生,由此造成重大的人员伤亡事故和不良的社会影响,严重制约着煤炭工业的健康发展。因此,研发煤矿探测机器人是煤矿井下发生瓦斯爆炸事故后进行抢险救援的前提手段和必要工具,对煤矿安全生产、减少国家和人民生命财产的损失具有十分重要的意义。本课题的研究得到了山西省科技攻关项目的资助,其中煤矿井下搜救探测机器人运动装置已获得国家发明专利。

煤矿巷道本身是一个非常复杂的三维非结构化环境,特别是矿难发生后,原有结构往往遭到不同程度的破坏。煤矿探测机器人置身于这种复杂环境,必须具有一定的路径规划能力,即能够在有障碍物的工作环境内,寻找一条从起始位置到达目标位置的无碰路径,同时还要保证这是一条按照路径长度最短、能量消耗最少、使用时间最短等优化准则产生的最优路径。目前,求解机器人路径规划的方法有很多,与传统优化方法相比,遗传算法以其较强的全局优化能力和较高的搜索效率在解决此类问题中得到广泛的应用[1-6]。但是,以上方法仍然存在许多不足,如早熟现象、接近最优解时收敛较慢等[7],这将可能导致局部最优解的产生,并影响到在实时性要求较高的环境中的应用。笔者根据煤矿探测机器人路径规划本身的实际应用要求,结合遗传算法所具有的特点,对传统的遗传算法进行了改进：在机器人工作的复杂三维空间中,充分考虑到井下环境地形的高低变化,采用栅格法对其进行建模,并根据路径长度最短、能耗最少的评价指标设计了适应度函数。按照可变长度的染色体编码方式及随机指导式搜索策略来生成初始种群,保证初始阶段无障碍路径的产生。同时,针对传统遗传算法中存在的“早熟现象”和“收敛速度慢”等问题,将交叉算子和变异算子进行优化设计,从而使整个规划过程变得简单而有效。

1 规划空间的建模

路径规划算法所处理的空间是环境的抽象空间,而机器人的工作空间是一个现实的物理空间,所以建立环境模型即实现物理空间到抽象空间的映射是进行机器人路径规划的一个重要环节。煤矿探测机器人工作的空间为三维地形空间,其中任意一点的坐标可表示为(x,y,z),其中平面 xy采用由Howden W.E.提出的栅格法[8]进行划分,以栅格为单位记录环境平面信息,z值则表示高度信息。这样工作空间被量化成具有一定分辨率的栅格,栅格的大小以机器人自身的尺寸为准,直接影响着环境信息存储量的大小和规划时间的长短。栅格划分太大,环境信息存储量小,规划时间短,但分辨率会下降,路径规划不够精确;栅格划分太小,环境分辨率提高了,但环境信息存储量加大,规划时间长。因此,可以通过比较机器人、障碍物及工作空间的大小来确定栅格的尺寸与数目,既保证机器人能在工作空间中灵活运动,又尽可能地减少环境信息的存储量,缩短机器人进行路径规划的时间。

假设机器人工作在具有静态障碍物的环境空间中,障碍物的位置和大小已知,把障碍物边界向外扩展一个最小安全距离即机器人本体在长、宽方向上最大尺寸的1/2,这样机器人就可看作为一个质点。划分后的机器人工作空间如图1所示,自由空间和障碍物均可表示为栅格的集成。图1中,黑色区域表示障碍栅格;栅格内不含任何障碍物,则为自由栅格,用白色区域表示。栅格内的数字表示离散化后的高度信息[9]。

图1 机器人的工作空间

本文采用直角坐标法和序号法两种栅格的标识方法。

1)直角坐标法。在图1中,栅格图的左上角为坐标原点,X轴、Y轴的正方向分别为水平向右和垂直向下,坐标轴上的单位长度定义为栅格区间的大小,则任意栅格均可由其直角坐标(x,y)惟一确定。

2)序号法。在图1中,定义左上角第一个栅格序号为0,并按照从左到右、从上到下的次序栅格序号依次递增的方法,为每个栅格定义一个序号 N,则每个栅格与其序号一一对应。

上述两种表示方法具有如下对应关系：

其中,mod表示取N/10之余数,int表示取N/10之整数。

在下面的算法分析中,分别用到了这两种栅格标识法。其中,序号法用于机器人运动路径的表示,因为序号法表示简单直观,便于进行遗传操作,且比直角坐标法节省内存。而在规划路径评价时,为了便于计算路径长度,则依照上述对应关系将序号转换成直角坐标。

2 基于改进遗传算法的路径规划方法

2.1 染色体的编码方式

遗传算法的运算对象是表示染色体的符号串,染色体表示机器人在工作空间中的一条运动路径。由于机器人运动路径可变,为了直观地表示生成的各条路径,方便遗传算子的操作,文中采用可变长度的染色体编码方式,用序号法标识栅格,从起始位置到终点位置由不同栅格序号连接起来的符号串即可描述一条路径。如图2所示,若设起点为0,终点为99,则图中所示的一条可行路径可以用符号串(0,10,21,31,42,52,53,64,65,76,77,78,88,98,99)加以描述。

2.2 初始种群的生成

遗传算法是对群体进行的进化操作,种群初始化是迭代运算的起点。为了保证算法能达到全局最优,初始种群应尽可能随机分布在搜索空间中每一个区域。若采用随机生成法,虽然能保持生成路径的多样性,但生成可行解的效率较低,因此本文用一系列随机生成与自由栅格构成的路径连接起点和终点,产生一条无障碍路径,有效地保证了生成路径的可行性,减少了初始种群产生的困难和盲目性。

2.3 适应度函数的设计

遗传算法中以适应度函数表明个体的优劣程度,从而决定其遗传机会的大小,直接影响到遗传算法的计算效率。结合实际情况,本文以路径长度和能量消耗作为评价指标,目标是找到这样一条路径：从起点到达终点的距离即路径长度最短,同时从起点到达终点的能耗也是最少的。因此个体适应度函数构造为

式中：α,β为权重系数,分别表示不同评价指标所占权重。令

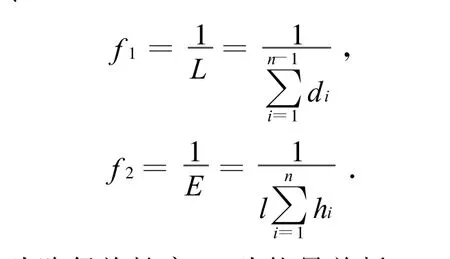
式中：L为路径总长度;E为能量总耗;d i表示路径中相邻两点的距离;hi表示路径中第i个栅格的高度;l表示栅格区间的大小。

2.4 遗传算子的操作

2.4.1 选择算子

选择操作采用De Jong K.A.提出的最优保存策略,也称为“精英保留”策略。其思想是把当前种群中适应度最高的个体完整地复制到下一代,并将下一代种群中适应度最小的个体淘汰,下一代种群中其余的个体则由轮盘赌选择法产生[10]。该策略的采用可以保证遗传算法迄今为止得到的最优个体不会因交叉、变异等遗传运算而破坏,它是遗传算法收敛性的一个重要保证,同时从理论上可以证明采用“精英保留”策略的标准遗传算法是全局收敛的[11]。

2.4.2 交叉算子

交叉操作是通过把两个父代个体的部分基因相互交换重组而生成两个新个体的操作,是遗传算法区别于其他进化算法的重要特征。本文采用单点和重合点混合的交叉方式。所谓重合点交叉是指对随机选取的两个个体,选择栅格序号完全相同的点进行交叉操作,当重合点多于一个时,随机选择其一进行交叉。若没有重合点,则随机选择交叉点进行单点交叉。显然常规交叉操作易产生间断路径,而重合点交叉不会产生新的断点。

2.4.3 变异算子

变异操作在改善局部搜索能力和维持种群多样性,防止出现早熟现象方面起着关键的作用。在传统遗传算法中采用的是随机变异操作,并没有对已知的环境信息加以利用,于是变异常常导致路径劣化。为此,笔者采用改进型变异算子,利用局部启发式搜索技术,保证变异后的节点必须在待变异节点相邻的自由区域内,且在路径的前进方向上,从而避免了变异的盲目性,以此来提高变异后生成新路径的连通性及算法的收敛性。

2.5 算法终止条件

本文采用遗传算法中常用的规定进化代数和设定收敛条件相结合的复合准则。当遗传算法满足设定的收敛判断条件时,算法终止;若达到规定进化代数但仍未满足设定的收敛判断条件,算法也将终止。其中设定算法的收敛条件为：若连续进化五代后,最优解均未发生变化,且适应度函数值提高不足1%。

3 仿真实验结果

遗传算法中运行参数的选择非常关键,控制参数的不同选取会对算法收敛性和最终解的质量产生直接影响。考虑到本文在初始种群生成时已采取一定的优化措施,因此,种群规模可取较小值,M=30;规定终止进化代数G=50。由于在交叉、变异等遗传算子的设计中,采取一系列的措施保证了产生的个体路径的有效性,所以交叉概率p c和变异概率pm的取值较大(其中pc=0.9,pm=0.1),以提高算法的全局搜索能力。

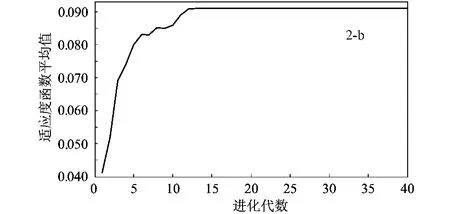
图2 改进遗传算法的仿真结果

为了研究改进遗传算法的正确性和有效性,并与采用单点交叉和随机变异的传统遗传算法进行比较,本文在10×10栅格的规划空间进行了仿真实验,结果如图2、图3所示。图中S和G分别表示机器人运动路径的起点和终点,折线表示算法所产生的最优路径。图2-a、图3-a分别表示改进遗传算法和传统遗传算法找到的最优路径,图2-b、图3-b分别表示改进后和改进前的群体适应度函数平均值随着进化代数的收敛情况。图中结果显示,采用笔者提出的改进遗传算法,进化约进行了12代后已达到收敛,而传统遗传算法则需要进化17代,说明改进算法具有很高的收敛速度。

图3 传统遗传算法的仿真结果

另外,本文还对随机运行60次的实验结果进行统计,从最小成功收敛代数、平均收敛代数及最优解出现概率等方面对算法的性能进行比较,结果如表1所示。

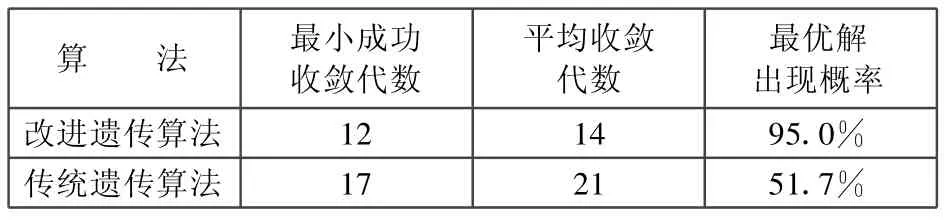
表1 算法的性能比较

可以看出,改进后的遗传算法较改进前在收敛性能和搜索效率上都有很大提高。

4 结束语

笔者针对煤矿探测机器人的实际应用要求,在三维空间中对机器人工作环境进行建模,采用了可变长度的染色体编码方式,使用随机指导式搜索策略来生成初始种群,保证初始阶段无障碍路径的产生,降低了算法的复杂性。根据路径长度最短且能耗最少的评价指标设计了适应度函数,有效地利用了路径规划中的地图信息。对遗传算法中的交叉和变异算子的优化设计,解决了传统遗传算法“早熟现象”和“收敛速度慢”的问题。仿真实验证明了本文所提算法的有效性和可行性,后续的主要工作是结合煤矿探测机器人的工作情况,将改进的算法应用到实际当中,并对提高算法的效率和收敛速度进行进一步的研究。

[1] 孙树栋,曲彦宾.遗传算法在机器人路径规划中的应用研究[J].西北工业大学学报,1998,16(1)：79-83.

[2] GERKE M.Genetic path planning for mobile robots[C]∥IEEE.Proceedings of the 1999 American Control Conference.San Diego ：IEEE Press,1999 ：2424-2429.

[3] Hu Y,Yang S X.A knowledge based genetic algorithm for path p lanning of a mobile robot[C]∥IEEE.Proceedings of the 2004 IEEE international Conference on Robotics and Automation.New Orleans：IEEE Press,2004：4350-4355.

[4] 王强,姚进,王进戈.基于遗传算法的移动机器人的一种路径规划方法[J].哈尔滨工业大学学报,2004,36(7)：867-870.

[5] TU J,YANG S.Genetic algorithm based path planning for a mobile robot[C]∥IEEE.Proceedings of the 2003 IEEE International Conference on Robotics and Automation.Taipei：IEEE Press,2003 ：1221-1226.

[6] OSCA RCastillo,LEONA RDO Trujillo.Multiple objective genetic algorithms for path planning optimization in autonomous mobile robots[J].Soft Computing,2007,11(1)：269-279.

[7] 雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社,2005.

[8] HOWDEN W.E.The sofa p roblem[J].The Computer Journal,1968,11(3)：299-301.

[9] 师黎,邵国.改进遗传算法用于移动机器人路径规划[J].计算机工程与设计,2008,29(24)：6330-6333.

[10] DE JONG K A.An analysis of the behavior of a class of genetic adaptive systems[D].Michigan：University of Michigan,1975.

[11] RUDOLPH G.Convergence analysis of canonical genetic algorithms[J].IEEE Trans on Neural Networks,1994,5(1)：96-101.