基于在险值的证券投资风险度量与管理

蔡基栋

（武汉大学经济与管理学院，湖北武汉430072）

基于在险值的证券投资风险度量与管理

蔡基栋

（武汉大学经济与管理学院，湖北武汉430072）

在险值是国际金融市场上通用的度量证券价格风险的工具，在金融机构风险管理中得到广泛应用。本文分别就单一证券资产和证券资产组合讨论了风险度量方法，总结了不同市场条件下在险值的计算公式。金融机构根据其业务种类和所分析的资产组合类型，选择合理的时间范围，计算出单个资产或证券价格指数的在险值，在此基础上计算出整个资产组合的在险值。为了降低证券资产组合价值的波动性，金融机构应尽量选择那些负相关、不相关或正相关程度不高的防御性证券进行组合投资。

在险值；标准差；证券价格风险；有效投资管理

证券价格的变化或者说波动性是客观存在的。在一个有效的证券市场上，证券价格是其内在价值的真实反映，而证券内在价值的确定与该证券预期收到的未来现金流及其不确定性有关。关于该证券的市场预期发生了改变，证券价格就会发生变化。影响证券市场预期的因素实在太多，包括政治的、经济的甚至心理的因素。从某种程度上来说，证券价格的风险远大于一般商品价格的风险。因为一般商品的价格（或者说价值）取决于生产该商品的社会必要劳动时间也就是劳动生产率，从短期来看，一般商品价格是相对稳定的（石油、贵金属等不可再生的稀缺资源除外）。但是就证券价格而言，即使在短期内也可能是不稳定的。因此，金融机构必须清醒地认识到证券价格风险的客观存在性，采取合适的方法进行度量，在准确度量的基础上进行有效的管理。目前对证券价格风险进行度量的主要工具就是在险值（Value at Risk，VaR）。由于证券价格的变化必然导致证券投资收益率的变化，或者说，证券投资收益率的变化实质是证券价格变化的真实反映。因此，在下面的模型分析中，大都是对证券投资收益率进行运算，如有必要，再转换成证券价格。

一、单只证券风险的度量

1．非参数方法

在不要求对证券收益率的概率分布作出假设的情况下，可以运用非参数法来计算在险值。例如，我们可以选择过去1001个交易日的收盘价格作为历史数据来计算95%置信度下的每日在险值，计算需采取以下五个步骤：

第一步：把1001个收盘价数据转换成1000个证券收益率序列；第二步：利用这1000个历史单日收益率，得出证券收益率在一天内的1000个模拟变化值；第三步：把证券的模拟变化值排序，就可以看出频度分布形状；第四步：找出全部模拟值最“左侧”的5%，即最“左侧”的50个模拟值；第五步：步骤4找到的对应于横轴上收益率的绝对值就是日在险值。

2．参数方法

在事先已知或假设资产收益率概率分布的情况下，可以运用参数法来计算。通常我们假设资产收益率的概率密度函数服从正态分布。

在正态性假设下，单一证券的在险值可以用一个简单易记的公式计算：

其中，α是与所选的ω概率水平相对应的标准正态分布Z值（例如，如果ω＝5%，则α＝1.645；如果ω＝2.5%，则α＝1.96；如果ω＝1%，则α＝2.33），σ是给定时间范围内证券收益率的标

3．含δ因素的在险值方法

通常情况下，证券价格的变化与证券市场指数的涨跌密切相关，我们可以把指数的变化看作证券价格变化的主要风险因素。不同的证券，其价格变动随指数变动的程度是不一样的，有的证券价格波动幅度高于指数波动幅度，有的则要低一些。用来衡量一只证券的收益率随整个市场指数收益率变动程度的指标就是δ参数。在只有证券市场指数这一个风险因素的情况下，计算单只证券在险值的解析式为：

其中σRF是给定时间范围内证券市场指数收益率的标准差，δ是该只证券特定的δ参数，其余指标的含义同上。

二、证券组合风险的度量

现代投资组合理论认为，证券组合的风险不是组合间单只证券风险的简单加总，它还取决于证券本身之间价格变动的协方差。一般来讲，一个证券组合的在险值要小于组合中所有单只证券的在险值之和。[1]这一点很容易通过现代投资组合理论模型加以验证。

在正态性假设下，证券组合的在险值同样可以用公式（1）加以度量，只不过这里的σ是给定时间范围内证券组合收益率的标准差，P是证券资产组合的当前市场价值。

若已知单只证券的在险值以及单只证券两两之间收益率变动的相关系数矩阵Σ，则证券资产组合的在险值也可通过下式计算：

其中X是单只证券在险值构成的列向量。

根据证券资产的两个基本定价模型即市场模型和因素模型，可以直接测算出证券资产组合的市场风险大小。

1．基于市场模型证券组合的风险度量

单只证券或组合的收益率与市场组合收益率之间的关系，可以通过下面的特征线来确定：

βP是证券组合的β系数，它相当于单只证券的δ参数。

2．基于因素模型证券组合的风险度量

因素模型认为，决定单只证券或组合收益率的因素有多个，而且满足线性关系：

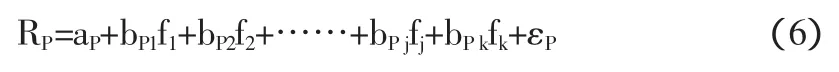
其中bPj表示证券组合P对第j个因素的敏感性。

对于一个充分分散化的证券组合来说，证券组合收益率的方差σp2=δ'Σ1δ，其中δ是因素敏感性bPj组成的列向量，Σ1是因素模型风险因子之间的方差—协方差矩阵。直接应用标准的在险值计算公式得到：

例如，假定一家中国银行买入了一笔以美元计价的10年期美国长期国债，价值1000万美元。风险管理经理想计算该国债1年期、95%置信水平的在险值。该头寸面临外汇风险和利率风险，我们将分别计算这两类风险的在险值，然后把风险加总得出反映外汇风险和利率风险唯一的在险值。计算时采用参数法，假设风险因素的变动服从正态分布。

首先，计算外汇风险及相应的在险值（记为VaR1）。风险因素是人民币/美元汇率，其变化的1年期标准差σ=0.3%。由于汇率变化能完全影响头寸的价值，所以δ=1，应用公式（2），可以得到：

VaR1=1.65×0.3%×1×10000000×8=396000（元）

假设当前汇率为1美元兑换8元人民币。

现在计算与利率风险有关的在险值（VaR2）。假定美国国债按面值计价，修正持续期（即本例中的δ参数）为7.3年，收益率1年期的波动性为0.4%，则对VaR的计算如下：

VaR2=1.65×0.4%×7.3×10000000×8=3854400（元）

该银行持有美国国债的多头头寸，因此面临利率和汇率双重风险，如果利率（债券的风险因素）变动与人民币/美元汇率变动的相关系数为0.2，则组合的VaR计算结果为：

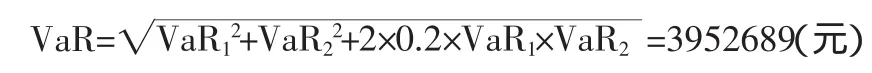
分散化的作用体现在未分散组合的在险值（VaR1和VaR2的简单加总）和组合分散后的在险值之间的差额（4250400-3952689=297711）。在证明资产分散化的作用时，我们选择了一种资产面临两种风险的例子而未选两个或两个以上不同的资产，其实这并不影响结论。在险值的核心在于（只要有可能）把组合中任一资产的风险分解成更简单的基本工具。因此，同时受利率风险和外汇风险影响的美国债券可以分解成两种更简单的工具，一种只受利率风险影响，另一种只受外汇风险影响。该美国债券于是可视为一个组合，由多头持有一只以人民币计价的固定利率债券和多头持有一只受外汇风险影响的美元计价的资产组成。

通过单一资产风险加总得出组合风险这一过程不仅限于两种资产，而且可以一般化适用于多种资产的情形。以下用一个例子显示分散化对一个多种资产构成的组合起了何等作用。表1给出了一家中国银行账户上的资产状况。

以下我们将基于风险因素变动服从正态分布的假设，运用参数法计算在险值。每种风险因素的1年期标准差给定。

假设人民币与美元之间的当前汇率为1美元兑换8元人民币，每种资产的在险值单位用人民币表示。公式（2）可以算出每种资产的在险值，如表1最后一列所示。

在计算整个组合的在险值时，必须考虑每对风险因素之间的相关性。这一步运用矩阵形式就可以简明清晰地表达出来。令X为单个资产在险值向量，Σ为风险因素相关矩阵，则整个组合的在险值用公式（3）计算：

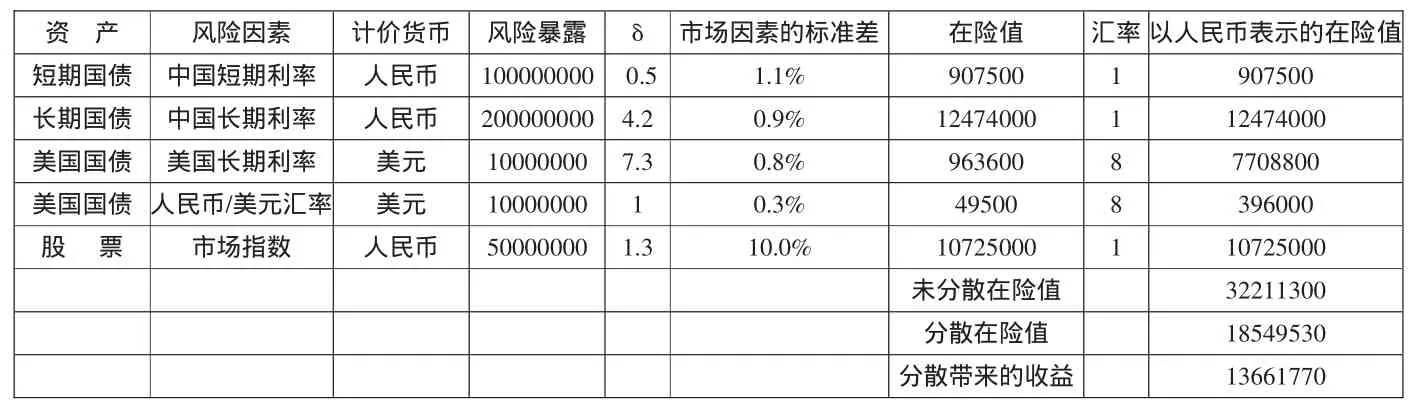
表1 计算金融资产组合的在险值

其中X'=[907500，12474000，7708800，396000，10725000] Σ值见表2。

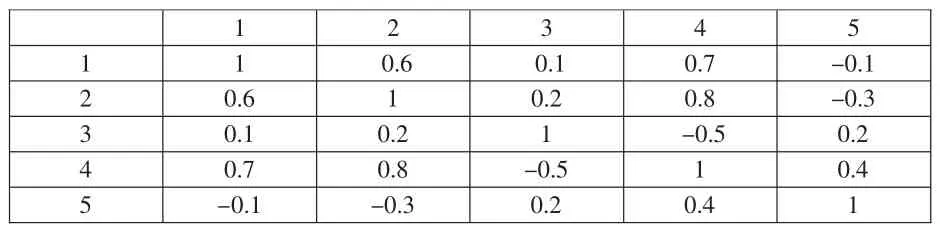
表2 风险因素的相关性矩阵

整个组合的在险值为18549530（95%置信水平，1年期），显著低于组合未分散下的在险值，后者高达32211300。分散化带来的好处是上两者之差即13661770。显然，如果每对风险因素的相关系数为1，那么组合分散与否在险值都是一样的，这也是马科维茨组合理论的观点。[2]

三、证券价格风险管理

由于在险值反映了给定的置信水平和目标时段下证券资产价值预期的最大损失，也就是最坏情况下的损失，这与市场参与者日常理解的风险概念是一致的。因此，在险值正确地度量了证券资产价值的风险。为了降低证券资产价值的风险，需要对证券资产进行有效管理。

1．根据金融机构的业务种类和所分析的资产组合类型，选择合理的时间范围。对于资产组合主要投资于高流动性货币市场工具的银行，最好选择1天为一个时间段。对于需按季度调整组合并报告业绩的投资基金经理来说，90天是比较合适的。理想的情况是时间范围与组合定期清算所需的最长时间相一致，如果时间范围短于组合定期清算所需的时间，则必须把流动性风险明确反映在模型之中。

2．在正确选择概率水平和期望收益率概率密度函数的基础上，计算单个资产或证券价格指数的在险值。根据金融机构对风险的理解，可选择5%或者1%的损失概率作为极端情形。一般情况下，可假定期望收益率的概率密度函数为正态分布。采用正态分布是因为几乎所有已知的推论性统计方法出发点都是正态假设，它在理论上已经过中心极限定理的证明。

3．计算出单个资产的在险值后，经过前面公式计算出资产组合的在险值。用这一在险值就可以评估金融机构在极端市场情形和目标时段下证券资产组合价值可能遭受的最大损失。

通过前面单个资产和资产组合在险值的计算公式可知，在险值的大小主要取决于单个资产和资产组合的标准差。从单个证券资产来讲，降低收益率波动性的方法是选择那些防御性证券进行投资，如有关的证券发行公司生产的产品或提供的服务有稳定的市场占有率，需求量对经济周期的敏感性较低；公司成本结构合理，经营杠杆和财务杠杆较小。从证券资产组合来讲，降低收益率波动性的方法是尽量选择那些负相关、不相关或正相关程度不高的证券进行组合投资。[3]如果风险证券的正相关程度都很高，降低证券组合风险的办法是加大无风险证券的投资比例，因为无风险性证券的收益率与所有风险证券的收益率不相关。

[1]Jorion Philippe.Portfolio Optimization in Practice[J].Financial Analysts Journal，1992，48（1）：68-74.

[2]Edwin J.Elton，Martin J.Gruber，Stephen J.Brown，William N. Goetzmann.现代投资组合理论与投资分析[M].北京：机械工业出版社，2008：45-46.

[3]胡昌生，熊和平，蔡基栋.证券投资学[M].武汉：武汉大学出版社，2009：118-119.

责任编辑：林英泽

Abstract:VAR is a main tool available for the risk measurement of the security price in the international financial markets.It is used popularly in the risk management of financial institutions.This paper discusses the risk measurement methods on a single security asset and securities portfolio respectively，summing up corresponding formula under different market conditions.According to the business types and the types of asset portfolio analyzed，financial institutions select a reasonable time frame.They calculate VAR of individual asset or securities price index.On the basis of preceding calculation，they work out VAR of the asset portfolio.In order to decrease the fluctuation of asset portfolio value，financial institutions should select those defensive securities with negative correlation，non-correlation or low positive correlation in securities portfolio investment.

Key words:VAR；standard deviation；risk of security price；effective investment management

A Research on the Relationship between Competitive Strategy and Performance

CAIJi-dong
（Economic and Management School of Wuhan University，Wuhan，Hubei430072，China)

F830.91

A

1007－8266（2010）10－0078－03

蔡基栋（1968-），男，湖北省武穴市人，武汉大学经济与管理学院证券投资教研室主任、博士生，主要研究方向为投资学、金融工程。