关于对称多项式的构造及其应用
何 灯
(福建省福清港头中学,福建 福清 350317)
关于对称多项式的构造及其应用
何 灯
(福建省福清港头中学,福建 福清 350317)
通过构造对称式和轮换对称式的一般表示式,借助于Maple应用程序,研究了3元到15元的对称多项式的缺项多项式、轮换对称代换缺项多项式、Si类对称多项式及Si类差分代换缺项多项式的通式构造,并对多元多项式的平方分拆进行了探讨.
对称多项式;缺项多项式;Si类多项式;平方分拆;机器证明
0 引 言
文献[1]通过构造对称式和轮换对称式的一般表示式,借助于Maple应用程序,研究了Si类多项式和缺项多项式,实现了3元到8元的缺项多项式和Si类多项式通式的构造.这些应用程序为我们研究多项式的性质提供了方便.但由于这些程序通用性较差,有些模块效率不高,部分表达式不能自动构造,如果用其研究更多元的情况将会发生困难.本文以文献[1]为基础,对对称多项式的一般式构造及其应用进行进一步探究,通过通用算法得到了3元到15元(15元以上的,机器的运算效率明显降低)的对称多项式的一般构造程序,并举例说明其在构造缺项多项式和Si类对称多项式的通式、多项式的平方分拆中的应用.
1 对称多项式和轮换对称多项式的一般表示
1.1 对称多项式一般表示式及其实现程序
n元初等对称多项式是指型如:
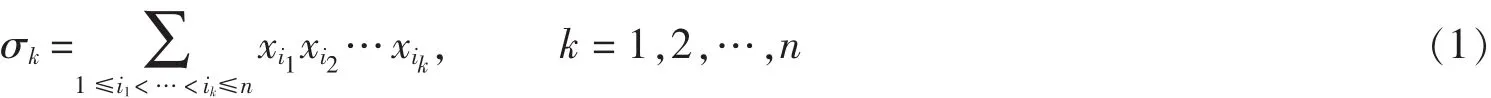
的对称式.由对称多项式基本定理[2]知,任何一个对称多项式均可用初等对称多项式表示出来,这样可以利用基本定理构造对称多项式的一般式.对于变元数较少的情况,文献[1]给出了构造程序pe[3](3元到8元对称多项式构造程序).为了研究更多元对称多项式的性质,需要编写多元初等对称多项式的通用构造程序.以下简要说明寻找σi的两个可行算法.
算法1 展开(x1+x2+…+xn-1+xn)i,寻找其中含有i个变元的项,将这些项去系数,相加,则可得σi.
算法2 求集合{x1,x2,…,xn}的子集,寻找其中含有i个元素的子集,将单个子集内的各个元素相乘,再将得到的因式相加,可得σi.
采用算法1,笔者编写了n元初等对称多项式的构造程序ddn(本文所编写程序均集中在参考文献[4]dcdxs中),命令格式是ddn(n).要构造一个n元m次的对称多项式的
1.2 轮换对称多项式一般表示式及其实现程序
文献[1]基于推广的多项式基本定理,给出了3元和4元的轮换对称多项式通式,对于多元的情况,由于还没有得到初等轮换对称式,从而通式构造遇到了困难.本文通过构造普通多项式的一般式,再根据轮换对称多项式的定义构造并解方程组,解决了这个问题.



依照这些命令序列,可以编写轮换对称多项式的一般式构造应用程序ldcts,其命令格式是ldcts(var,deg),其中var是变元个数,deg是次数.
例1 试确定6元3次轮换对称多项式一般式.
解 运行ldcts(6,3),则得(其中ki为待确定参数,若取其为特殊值,则可得特殊表达式,下同):

2 缺项多项式
文献[1]定义了差分代换缺项多项式.由于缺项多项式在差分代换后降低了维数,更便于研究,故研究这类多项式是有意义的.文献[1]中的程序up[3]能够得到3元到8元对称多项式的差分代换缺项多项式通式.笔者在文献[1]的基础上,利用本文2.1中得到的对称多项式的一般式构造程序dcts,编写出了3元到15元的对称多项式差分代换缺项多项式通用程序dque,其运行命令是dque(var,deg),其中var为变元个数,deg为次数,输出一个含两个元素的数组,第一个元素是以σi表示的通式,第二个元素是以xi表示的通式.
例2 确定9元6次对称差分代换缺项多项式通式.
解 运行 dque(9,6)[1]([1]表示只需要输出 dque(9,6)的第一个数组元素, 下同), 则得:
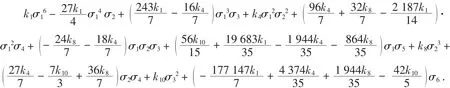
对于一个n元对称多项式f(x)=f(x1,x2,…,xn),由于各个变量所处的位置是平等的,故不妨设xn-1≥xn-2≥…≥x2≥x1≥xn,只需做一次如下差分代换:

从而可定义差分代换缺项多项式并由上代换确定其通式.对于一般的多项式,由于其各个变量不是平等的,故不能仅通过一次的差分代换确定其差分代换缺项多项式的通式.而对于一个n元轮换对称多项式,通常可设xn为变量中最小者,从而可作如下代换(与差分代换有区别):
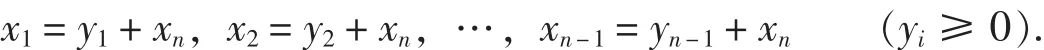
类似文献[1]差分代换缺项多项式的定义,我们可定义:
一个 n 元多项式 f(x) =f( x1,x2,…,xn), 作代换

后得到的代换式中, 如果缺少含有 Xn的项, 即 f(x1,x2,…,xn) =g( y1,y2,…,yn-1), 则称f(x)为轮换对称代换缺项多项式.
基于以上的定义,笔者编写了确定轮换对称代换缺项多项式程序lque,程序中用到了本文2.2中的轮换对称多项式的一般式构造应用程序ldcts,其算法类似于dque,命令为lque(var,deg),其中var为变元个数,deg为次数.由于4元以上的轮换对称缺项多项式通式比较复杂,限于篇幅,下面仅举两个简单例子说明lque的使用.
例3 确定4元5次轮换对称代换缺项多项式通式.
解 运行 lque(4,5), 则得:

其中,

例4 确定3元8次轮换对称代换缺项多项式通式,并找到其中一个半正定多项式.
解 运行命令lque(3,8), 则得:
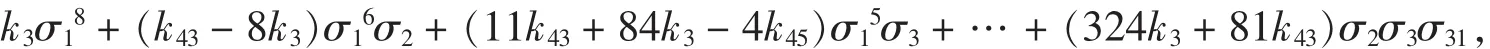
其中,
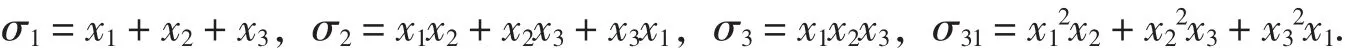
令k3=1,k43=-3,k45=7,得多项式可因式分解为:

显然非负.
3 Si类多项式通式
文献[5]定义了 Si类多项式: 如果 m 元 n 次齐次多项式 f≡ f(x1,x2,…,xm)满足f(1,1,…,1) =0, 并且当 m-i(m-1 ≥ i≥ 0)个变元相等时 f取值为零, 则称 f属于 Si类多项式.文献[1]实现了4元到8元Si类对称多项式通式的程序构造.本文利用对称多项式的一般式构造程序dcts编写出了3元到15元的Si类对称多项式通用程序Sidc,其运行命令是 Sidc(i,var,deg), 其中var为变元个数, deg为次数.
例5 确定13元12次S5类对称多项式通式.
解 运行 Sidc(5,13,12), 则得:
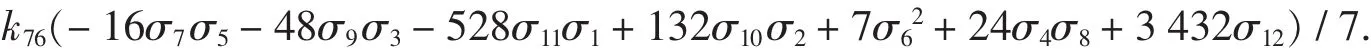
例6 确定最大i的11元12次Si类对称多项式通式.
解 运行 Sidc(5,11,12), 没有得到输出结果. 运行 Sidc(4,11,12), 得到:

这说明11元12次Si类对称多项式的最大i为4.
例7 确定最低元数的10次S4类对称多项式通式.
解 运行 Sidc(4,9,10), 没有得到输出结果. 运行 Sidc(4,10,10), 得到:

这说明10次S4类对称多项式的最低元数为10.
例8 确定最低次数的10元S3类对称多项式通式.
解 运行 Sidc(3,10,7), 没有得到输出结果. 运行 Sidc(3,10,8), 得到:
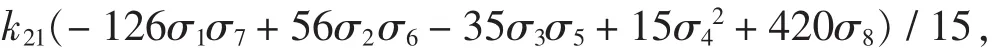
这说明10元S3类对称多项式的最低次数为8.
4 Si类差分代换缺项多项式通式
对多项式多一种考量的标准,我们就对多项式的性质多了一重认识.在Si类多项式及差分代换缺项多项式的基础上,笔者提出了Si类差分代换缺项多项式概念,将差分代换缺项多项式的通式构造程序dque和Si类对称多项式构造程序Sidc合并,可得Si类差分代换缺项多项式通式构造程序Sique,其运行命令是Sique(i,var,deg),其中var为变元个数,deg为次数,输出一个含两个元素的数组,第一个元素是以σi表示的通式,第二个元素是以xi表示的通式.
例9 确定9元8次S2类差分代换缺项多项式通式.
解 运行 Sique(2,9,8)[1], 得到:
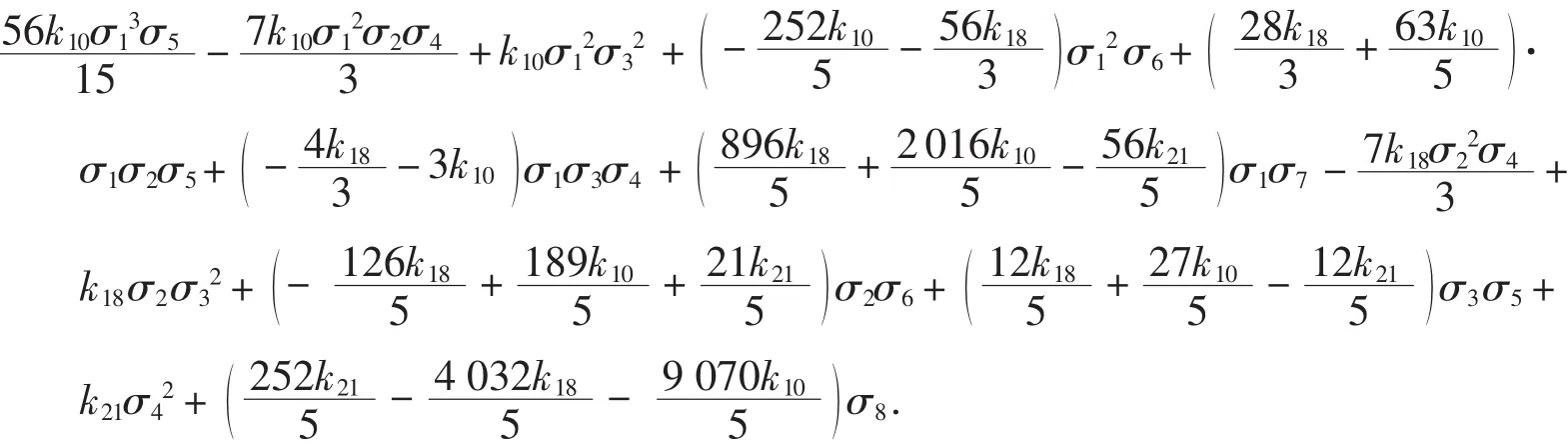
5 对称多项式的平方分拆
2006年文家金,张勇在文献[6]中解决了如下问题.
设实系数n元齐次对称多项式F(x)满足:当x1=x1=…=xn时有F(x)=0,且F(x)的次数不小于2.问:是否存在多项式P(i,j,x)使得:

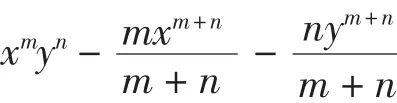

对于3元的xmynzt,由式(6)可得:
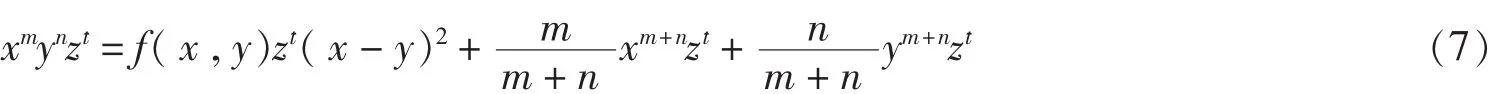
pfbs是由多个分块程序和一个主程序组成,第一个程序是基于式(6)编写的,其能够给出型如式(6)的分拆结果,第二个程序是基于式(7)编写得到的,其能够得到式(7)的分拆并利用第一个程序对2元的进行拆分,第三个程序用到了第二个程序,如此类推,得15个分拆程序,后面的每个程序均用到其前一个程序.主程序pfbs的作用是将输入的多项式的每个项都表示为Pi+Qi的形式,并把所有的Pi和Qi分别相加并对Qi合并同类项,若ΣQi=0,则输出ΣPi,完成分解,否则同时输出ΣPi和ΣQi.
例10 Mohab Safe(巴黎第6大学副教授)2009年提出了一个4变量24次1289项的大多项式[11],对其做平方分拆,运行如下命令:

在电脑d盘中得到了文件mm2.txt,里面给出了具体的分拆结果,详细可参阅文献[11].
例11 试验证8元6次以(1,1,…,1)为零点的轮换对称多项式总是能够进行平方分拆的.
解 先利用ldcts构造8元6次的轮换对称多项式一般式,记为tem,对各个变元赋值1,得到一个方程,解之代入tem中,记结果为temp,运行pfbs(temp).此过程可用如下命令自动完成:

在输出的结果中,由于非平方部分恒为零,故8元6次以(1,1,…,1)为零点的轮换对称多项式总是能够进行平方分拆的.
例12 试验证13元10次以(1,1,…,1)为零点的对称多项式总是能平方分拆.
解 利用dcts求13元10次对称多项式一般式,记为tem,对各个变元赋值1,得到一个方程,解之代入tem中,运行pfbs,过程可由如下命令完成:
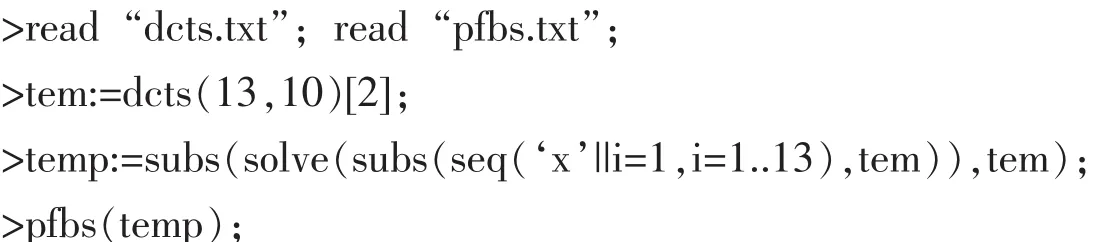
输出的分拆结果表明,13元10次以(1,1,…,1)为零点的对称多项式总是能够平方分拆的.
6 结 语
文献[1]通过构造多项式通式,对一些特殊类型的多项式进行研究,从而发现了多项式的一些性质或规律.本文沿用这一思路,得到了一些新算法,弥补了文献[1]程序的不足,从而提高了程序的运算效率和功能,延伸了应用范围.提出的轮换代换缺项多项式及Si类差分代换缺项多项式概念,丰富了多项式的研究类型.本文只是侧重于这些特殊类型多项式的构造,并未对其正性等性质进行专门研究.如何对这些多项式类型进行深入研究,揭示其特殊规律并应用到具体问题中,是一个十分重要的研究课题,有待进一步研究.
[1]刘保乾.对称多项式的一般表示式及其应用[J].广东教育学院学报,2010,30(3):17-24.
[2]姚慕生.高等代数学[M].上海:复旦大学出版社,2005:198-199.
[3]xzlbq(刘保乾).对称多项式的一般表示式及其应用[EB/OL].http://www.irgoc.Org/viewtopic.php?f=27&t=658&sid,2010-06-03.
[4]hedeng123(何灯).对称多项式构造程序dcdxs[EB/OL].http://www.irgoc.Org/viewtopic.php?f=27&t=721&sid,2010-07-02.
[5]刘保乾.Si类多项式初探[J].广东教育学院学报,2007,27(5):6-13.
[6]文家金,张勇.齐次对称多项式的分解原理与方差平均不等式猜想[J].四川师范大学学报,2006,29(4): 438-442.
[7]刘保乾.多元齐次对称生成分拆基初探[J].广东教育学院学报,2006,26(5):5-15.
[8]何灯.3元n次对称多项式的平方型分拆及其他[J].佛山科学技术学院学报,2010,28(4):51-57.
[9] 刘保乾.再谈多项式的平方分拆[J].佛山科学技术学院学报,2010,28(5):43-50.
[10]xzlbq(刘保乾).何灯老师请注意——平方型分拆可否有重要进展[EB/OL].http://www.irgoc.Org/viewtopic.php?f=27&t=480&sid,2010-03-22.
[11]yanglu(杨路).Safey的大多项式你们的方法能做吗?[EB/OL].http://www.irgoc.org/viewtopic.php?f=27&t=501&sid,2010-04-01.
Abstract:General expressions for constructing symmetric polynomials are proposed.In Maple, 3 to 15-term symmetric polynomials,permute symmetric polynomials, Sisymmetric polynomials and Sidifferential substitution polynomials with sparse terms have been constructed.Multiple-term polynomials have been studied in square decomposition.
Key words:symmetric polynomial; polynomial with sparse terms; Sipolynomial; square decomposition;machine proof
On Constructions and Applications of Symmetric Polynomials
HE Deng
(Gangtou Middle School, Fuqing 350317, Fujian, China)
O 122.3
A
1001-4217(2010)04-0001-08
2010-04-14
何灯(1984-),男,福建福清人,学士,教师,全国不等式研究会成员.研究方向:不等式的机器证明.E-mail:hedeng123@163.com

