两类特殊图的泛宽度染色
刘秀丽
(菏泽学院数学系,山东 菏泽 274015)
两类特殊图的泛宽度染色
刘秀丽
(菏泽学院数学系,山东 菏泽 274015)
研究了图染色问题中与频道分配有关的泛宽度染色.给出了两类特殊图的泛宽度色数.
泛宽度染色;d-宽度箱;泛宽度色数;双图
0 引 言
图论发展到现在已有许多分支,着色理论是其中之一,且有着极其重要的地位.它起源于150年前的四色猜想.染色问题在组合分析和实际生活中有着广泛的应用,是图论研究中一个很活跃的课题,近年来,又提出了许多新的染色问题在频道分配中的应用,如Bresar等人[1]提出了一种染色-泛宽度染色.在一个给定的网络中,使用相同广播频率的两个站点的信号将会相互干扰,除非它们的位置相当远.信号传播的距离与这些信号的功率直接相关.图的泛宽度染色是依据顶点之间的距离对顶点的一种剖分.对于不具有特定图结构的任意图来说,确定图中任意两个顶点的距离是非常困难的,而且在目前已知的结论中,也都是针对具有具体图结构的图类来研究的.如在文献[1]中作者给出了无限正方形和完全图Kn的剖分图s(Kn)的泛宽度色数.Scoper[2]研究了树的泛宽度染色,证明了无限3-正则图树的泛宽度色数是7.张珊珊等人[3]研究了轮、扇及完全图Kn的推广的hajos sum泛宽度染色,并在另一文献[4]中研究了圈及其相关图的泛宽度染色.在文献[1]中作者猜想:确定任意图的泛宽度色数问题是NP(有非确定性多项式算法)完备问题.本文研究了两类双图的泛宽度色数.
文中未加说明的记号和术语参见Bondy等人文献[5-6].
1 预备知识
我们用V(G)和E(G)分别表示图G的顶点集和边集.设G是一个简单图,对于任意两个顶点x,y,它们的距离d(x,y)是x-y路长的最小值,特别地,如果没有x-y路,则 d(x, y)= ∞.
定义1[1]设G=(V(G),E(G)),d是一个正整数,X是V(G)的一个子集,如果X中任意两个点的距离都大于d,称X是一个d-宽度箱,d叫做X的宽度,显然,d-宽度箱也是(d-1)-宽度箱、 (d-2)-宽度箱等等.
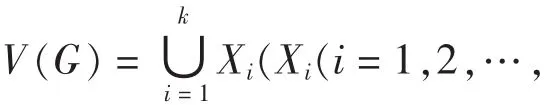
显然,此处我们的目的是最小化k,可以假设对每个整数i,Xi是一个i-宽度箱.
定义 3 设 G 和 G′均为简单连通图, V(G) ={v1,v2,…,vn}, V(G′) ={u1,u2,…,un}.在 G 和 G′之间加匹配 viui(i=1,2,…,n), 得到新图 D(G), 我们称 D(G)为 G 的双图.于是:
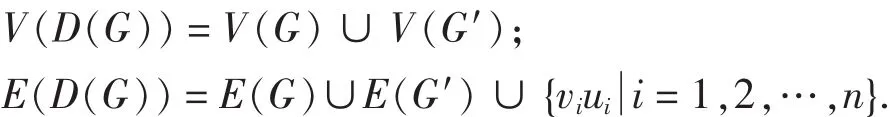
2 主要结果及证明
定理 1 设 Pn, P′n为两条长为 n-1 的路, 其顶点集分别为 V(Pn) ={v1,v2,…,vn}和V(P′n) ={u1,u2,…,un}, 则当 n>5 时, 有 χρ(D(Pn)) = 5.
证明 首先证明 χρ(D(Pn)) ≥ 5.
反证法,假设有一个映射 f: V(D(Pn)) → {1,2,3,4}.对于 D(Pn)上的各个顶点,除了v1u1,v2u2,…,vnun之外都是对称的,不妨令f(u2)=1.因为:
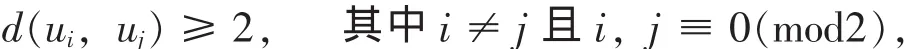
所以可以用 1 来染 uj(j≡ 0(mod2)), 即当 j≡ 0(mod2)时, f(uj) = 1; 又因为:
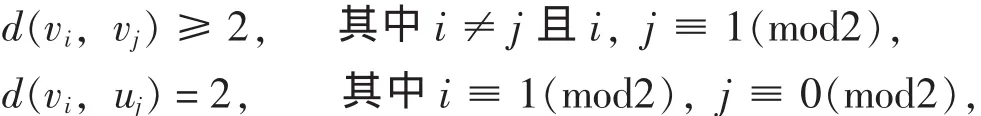
所以可以用 1 来染 vi(i≡ 1(mod2)), 即当 i≡ 1(mod2)时, f(vi) = 1.
对于剩余的未染色的顶点,不妨令f(v2)=2.因为:
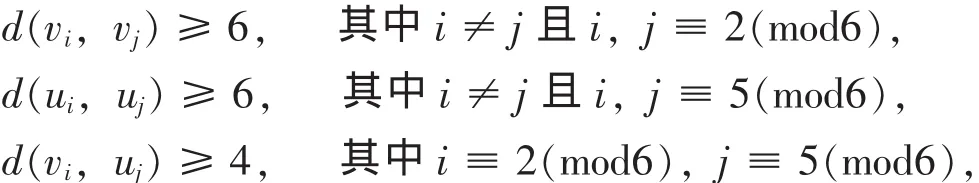
所以可以用 2 来染 vi,uj(i≡ 2(mod6), j≡ 5(mod6)), 即当 i≡ 2(mod6),j≡ 5(mod6)时, f(vi) = 2, f(uj) = 2.
类似可以用 3 来染 vi,uj(i≡ 4(mod6), j≡ 1(mod6)), 即当 i≡ 4(mod6), j≡1(mod6)时, f(vi) = 3,f(uj) = 3.
此时还剩余形如 vi(i≡ 0(mod6))和 uj(j≡ 3(mod6))的点未染,但是 d(v6,u3) = 4,不能用4同时染v6和u3,所以还需要用另一种新的颜色.
类似可以证明其他的染色方式也不行.所以,χρ(D(Pn))≥ 5.
再证 χρ(D(Pn)) ≤ 5.
下面构造一个映射 f: V(D(Pn)) → {1,2,3,4,5}.
当 i≡ 1(mod2)时, 令 f(vi)= 1; 当 i≡ 0(mod6)时, 令 f(vi) = 5;
当 i≡ 2(mod6)时, 令 f(vi) = 2; 当 i≡ 4(mod6)时, 令 f(vi) = 3;
当 j≡ 0(mod2)时, 令 f(uj) = 1; 当 j≡ 1(mod6)时, 令 f(uj) = 3;
当 j≡ 3(mod6)时, 令 f(uj) = 4; 当 j≡ 5(mod6)时, 令 f(uj) = 2.
易证映射 f是 D(Pn)的一个泛宽度染色, 所以 χρ(D(Pn)) ≤ 5.
综上, 当 n>5 时, 有 χρ(D(Pn)) =5.
注 1 特别地, 当 n=3, 4, 5 时, χρ(D(Pn)) = 4.
定理 2 设 Wn, W′n为两个轮, 其顶点集分别为 V(Wn) ={v0,v1,v2,…,vn}和 V(W′n) ={u0,u1,u2,…,un}, 则 χρ(D(Wn))= n+2.
证明 首先证明 χρ(D(Wn)) ≥ n+2.
由图D(Wn)的结构易知,图D(Wn)中最长的是 P4,即图D(Wn)中任意两点之间的距离都小于等于3,那么最多只有颜色1和2可以染多个顶点,其余的颜色只能用来染一个顶点.相互之间距离大于等于2的顶点构成D(Wn)的独立集,易知,图D(Wn)的最多独立集I满足满足任意两点相互之间的距离大于等于3的顶点集中只有两个顶点,因此需要颜色数大于等于2n+2-n-2+2=n+2,即χρ(D(Wn))≥ n+2.
再证 χρ(D(Wn))≤ n+2, 即用 n+2种颜色可以完成对图 D(Wn)的泛宽度染色.
用1来染最大独立集I中的顶点,用2来染剩余未染的并且满足距离大于等于3的顶点,对于剩余的2n+2-n-2=n个顶点,因为相互之间的距离都小于等于3,所以n个顶点可以用n种染色来染,染完D(Wn)的所有顶点一共用了n+1+1=n+2种颜色.所以, χρ(D(Wn)) ≤ n+2.
综上, 有 χρ(D(Wn)) = n+2.
注2 图的泛宽度染色是依据顶点之间的距离对顶点的一种剖分.对于不具有特定图结构的任意图来说,确定图中任意两个顶点的距离是非常困难的,而且目前已知的结论中,也都是针对具有具体图结构的图类来研究的,并且在文献[1]中作者也猜想:确定任意图的泛宽度色数问题是NP完备问题.
下面构造一个算法来实现对任意图的泛宽度染色.
思想 在第i步从那些未染色的点中,找一个极大的i-宽度箱Xi,把Xi中所有的顶点染颜色i,指标i从1开始,每一步增加1,用k表示i的最终值.
算法

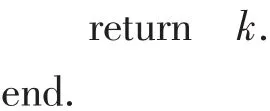
从这个算法可以很容易得出,对于任意图G,有χρ(G)≤k.在第一步中,当i=1时,V中极大的1-宽度箱就是图G的最大独立子集I,即X1=I,由此可以得到:
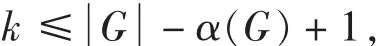
对于很稠密的图来说,上述式子可以取到等号,即:
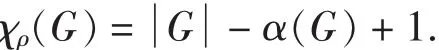
例如完全图Kn.
3 结 语
本文研究了由两条路以及两个圈构成的双图的泛宽度染色,并得出了这两类双图的泛宽度色数.本文的不足之处在于研究的图类简单,只给出了在两条路或两个圈之间加一重匹配.可考虑加多重匹配,还可进一步考虑研究其他图类的泛宽度色数.
[1]Bresar B,Klavzar S,Rall D F.On the packing number of cartesian products, hexagonal lattice,and trees[J]. Discrete Applied Mathematics, 2007, 155(17): 2 303-2 311.
[2]Scoper C.An eccentric coloring of trees[J].Australasia J Combin, 2004(29): 309-321.
[3]张姗姗,刘晓晓,陈丽华.几类特殊图的泛宽度色数[J].山东科学,2008,21(04):32-37.
[4]陈丽华,张姗姗,刘晓晓.圈及其相关图的泛宽度染色[J].山东科学,2008,21(05):75-78.
[5]Bondy J A, Murtyu S R.Graph theory with applications[M].London: Macmillan Press, 1976, 75-128.
[6]Bollobas B.Modern graph theory[M].New York: Springer-Verlag, 1998, 145-177.
Abstract:The packing coloring, to be related to frequency assignment problem of coloring problem,were deliberated.The packing numbers of two kinds of graphs were given.
Key words:packing coloring; d-packing; packing chromatic number; double graph
On the Packing Coloring of Two Kinds of Graphs
LIU Xiu-li
(Department of Mathematics, Heze University, Heze 274015, Shandong, China)
O 157.5
A
1001-4217(2010)04-0008-04
2009-09-30
刘秀丽(1977-),女,山东曹县人,讲师,硕士研究生.研究方向:图论与组合优化.E-mail:liuxiuli1004@163.com

