2D-C/SiC复合材料的拉伸损伤研究
杨成鹏, 矫桂琼, 王 波
(西北工业大学工程力学系,西安 710129)
连续纤维增韧陶瓷基复合材料(CFCCs)具有高比强度、高比模量、耐高温、抗氧化等许多优异性能,在航空航天领域具有广阔的应用前景。但是,材料的设计与使用必须以材料力学本构关系的研究为基础[1]。为了模拟计算材料的力学响应,需要了解基体的开裂性能,因为基体开裂会导致应力-应变关系的非线性,也会影响材料的强韧性[2]。同时,界面层对于材料性能的影响也是至关重要的,因为界面可以改变应力分布状态,使基体裂纹发生偏转,从而耗散更多能量,减小纤维应力集中程度[3]。然而,在纤维与基体之间沉积界面,相当于在纤维表面增加了涂层,可能会使纤维表面的缺陷增大,引入更高的应力强度因子,导致纤维就位强度降低[4]。试验研究表明[5,6],碳纤维的就位强度远远低于其原始强度。
本工作通过单调拉伸和循环加卸载试验研究了2D-C/SiC复合材料的拉伸性能和损伤演化过程,同时研究了残余应变和卸载模量与拉伸应力的关系,并建立细观力学模型对材料的应力-应变行为和极限强度进行了模拟计算。
1 试验方法
试验用2D-C/SiC复合材料由西北工业大学超高温复合材料实验室制备。将T300碳纤维束编织制成碳布,叠层为预制体,先在碳纤维表面沉积热解碳界面层,然后通过CVI工艺沉积碳化硅基体,制成纤维体积分数约为40%的复合材料平板,经过裁剪得到狗骨形试件,最后在试样表面沉积碳化硅抗氧化涂层。材料最终密度约为2.0g/cm3。
拉伸试样总共11件,两端均粘贴铝质带倒角加强片,防止局部压溃,以保证试验顺利进行。在INSTRON 5567试验机上进行常温单轴拉伸试验,采用位移控制方式加载,加载速率为0.2mm/min。为了研究材料在拉伸过程中的损伤行为,取其中4件进行了拉伸加卸载试验,卸载应力分别为50MPa,70 MPa,100 MPa,150 MPa和200 MPa。试验过程中,单调拉伸试验采用应变片测量应变,而加卸载试验过程采用标距为25mm的引伸计测量材料的实时拉伸应变。
2 试验结果
试样尺寸及其试验结果见表1,其中,L1~L7为单调拉伸试样,T1~T4为拉伸加卸载试样。根据应力-应变曲线在0~50 MPa之间线性阶段的斜率得出材料弹性模量的平均值为109.09GPa,而拉伸极限强度和断裂应变的统计平均值分别为258.20MPa和0.535%。

表1 试件尺寸和拉伸试验结果Table 1 Material dimensions and experimental results
单调拉伸应力-应变曲线如图1所示,曲线整体上表现出明显的非线性,类似于抛物线的形状。在拉伸应力达到50MPa之前,曲线具有较好的线性,材料几乎没有损伤。当载荷大于50MPa时,材料的模量逐渐降低,材料中的初始缺陷及裂纹开始增长并扩展,导致纤维与基体之间的界面产生脱粘和滑移,材料的应力-应变表现为非线性;在拉伸载荷超过150MPa以后,损伤进入稳定阶段,曲线再次表现出近似线性的特征。
拉伸加卸载应力-应变关系如图2所示,其中E为材料的初始模量,定义为加载起始直线段的斜率;Eu为卸载模量,定义为不同应力水平卸载后重新加载至该应力水平所对应的直线段的斜率;εr与εe分别为不同卸载应力所对应的残余应变和弹性应变[7]。从图中可以看出2D-C/SiC复合材料具有明显的力学迟滞效应,这是因为,卸载过程中,纤维束之间,以及纤维与基体之间的摩擦滑移会耗散部分能量[8]。而且,材料的卸载模量不断降低,残余应变逐渐增大,表明材料内部的损伤不断累积,直至材料断裂。
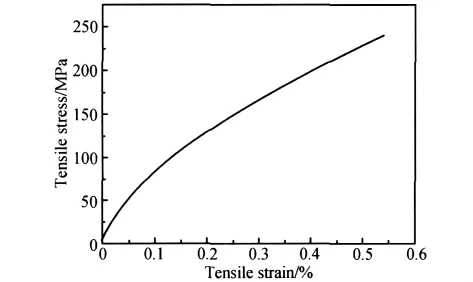
图1 2D-C/SiC拉伸应力-应变曲线Fig.1 Tensile stress-strain curve for 2D-C/SiC composites

图2 加卸载拉伸应力-应变曲线Fig.2 Loading and unloading tensile stress-strain curve
图3为弹性应变与残余应变关系曲线,图4为卸载模量与外加应力关系曲线。从图3可以看出,残余应变在低应力水平增加较快,而在较高应力水平增加较慢,甚至趋于线性增大,这一点与单调拉伸应力-应变曲线非常相似。图4也具有类似的特征,即卸载模量在较低应力时变化较快。这意味着,如果用残余应变和卸载模量来表征[9]2D-C/SiC复合材料的损伤变量,它与拉伸应力的关系曲线可近似为抛物线形式,下面将对此进行深入研究与讨论。本次试验结果与文献[7]得出的结论大不相同。
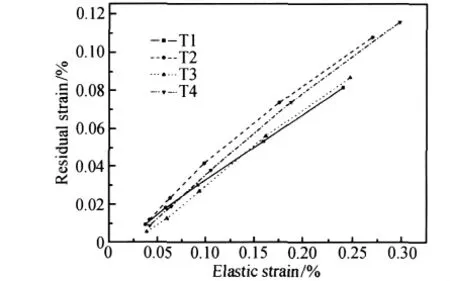
图3 残余应变与弹性应变的关系Fig.3 Residual strain vs elastic strain

图4 卸载模量与拉伸应力的关系Fig.4 Unloading modulus vs tensile stress
图5为试样的断口形貌,断口较平整,纤维拔出短;纤维束被明显地断裂拔出,可见纤维束之间为弱结合。试样T1和T2纤维束拔出数量较多,长度较长,结合表1可以看出其断裂强度较高[7];试样T3纤维束拔出不明显,断口平齐,应力集中影响较大,其拉伸强度较低;试样T4的断面沿长度方向有较大倾斜角度,层间开裂严重。结合表1、图3和图5可以看出,当试样断口位于引伸计刀口之外时(T1,T3),测量出的应变值较小,而当试样断口位于引伸计刀口之间时(T2,T4),测量出的应变较大,这说明试样在断裂区有较大应变集中,其原因可能是断裂区裂纹密度较大或者裂纹张开位移较大。

图5 2D-C/SiC试样断口Fig.5 Fracture sections of 2D-C/SiC specimens
3 损伤本构模型
从前面的试验结果可知,2D-C/SiC试样的残余应变和卸载模量与拉伸应力的曲线关系近似为抛物线形。文献[9]同样研究发现,损伤因子与应力的关系用抛物线进行拟合效果很好。
从细观上分析,材料的残余应变是由基体开裂和界面脱粘引起的,加载过程中,基体裂纹会张开,如果界面剪应力较大,卸载后,由于界面摩擦滑移阻力太大,裂纹将不能闭合,于是产生了不可恢复的变形。这种情况下,基体裂纹密度对残余应变的影响至关重要。由于测量方法的局限,裂纹的数量和分布状态会直接影响到测量值(图3)。
对于2D-C/SiC复合材料,由于组分材料的热膨胀系数不同,在制备过程中会产生很大的热失配应力,约为135MPa[9],因此产生了大量的初始裂纹。文献[10]研究后发现,初始裂纹间距的平均值L约为144μm,而文献[11]在模拟研究中取饱和裂纹间距同样为144μm。考虑碳化硅的断裂强度很高,约500 ~600MPa[5],这种情况下,只有 CVI工艺形成的原始孔隙才会成为裂纹源,而孔隙在较低应力时就会开裂。因此,本研究假定,热失配应力使材料中的裂纹趋于饱和,加载过程仅仅导致初始裂纹的扩展,不会产生新的基体裂纹。
如考虑基体裂纹的演化,裂纹间距L应该是外加应力σ的函数,这样会使模拟过程变得繁琐,而且这方面的研究文献很多,有大量的模型可供参考,这里不再考虑。根据以上分析,当界面结合较强时,材料的残余应变由裂纹张开位移δ和裂纹间距L决定,文献[12]根据能量平衡条件得出:
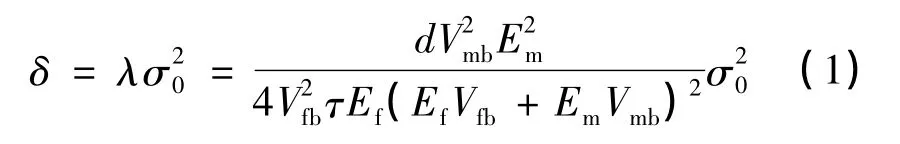
其中,d为纤维直径;Ef,Em分别为纤维和基体的模量;Vfb,Vmb分别为纤维束中纤维和基体的体积分数;σ0为纵向纤维束所承担的应力。若界面滑移阻力很大,则裂纹张开后将不会闭合,因此εr=δ/L,可见残余应变与纵向纤维束所承担的应力为抛物线关系。
设外加应力为σ,横向纤维束承担的应力σ90=κσ0,其中κ为载荷分配系数,取值为1,表明0°和90°铺层对复合材料的整体刚度具有等同作用;取值为零,意味着横向纤维束失去了承载能力,载荷全部由纵向纤维束承担。根据力平衡关系和等应变假设,可以得出:

其中,E0,E90分别为纤维束的纵向模量和横向模量。

其中,A,B分别为待定系数,E为单调拉伸加载的初始模量(图2)。于是试样的总应变ε=εr+εe就可以表示为:

上式是2D-C/SiC复合材料试样的单调拉伸应力应变关系式。然而,参数A和B需要通过试验测定,因此有必要建立理论模型来计算卸载模量。
将2D-C/SiC复合材料简化为0°,90°正交层合板。基体开裂后,在外加载荷的作用下,纤维与基体之间的界面会产生脱粘,使得材料的模量降低。界面脱粘长度m可以表示为[12]:
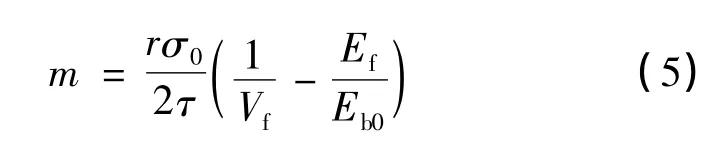
其中Eb0=EfVf+EmVm,是无损伤情况下0°层的模量;Vf,Vm分别为复合材料中纤维和基体的体积分数,r为纤维半径。损伤后,0°层的弹性模量,即卸载模量可以表示为[13]:其中定义为界面脱粘率,表征界面的损伤程度,η=0.5代表界面全部脱粘。由式(6)可以得出,卸载模量与应力的函数关系式为:


上式中,a和b为待定参数,式(7)并不是上文假设的抛物线形,但曲线形状类似,下文的模拟计算也表明采用式(3)和式(7)的模拟结果非常接近。设90°层损伤后的模量为E90u,则复合材料的卸载模量的表达式为:

基于以上分析,2D-C/SiC复合材料的理论损伤本构关系可以表示为:

4 模拟计算
依据试验,单向SiC/SiC,SiC/CAS和他们的正交铺层和平纹编织复合材料应力-应变曲线存在较明显的2倍比例关系[14],因此,本工作取载荷分配系数κ=0,即认为2D-C/SiC复合材料的单轴拉伸行为主要由纵向纤维束控制。
根据表2的材料参数,由式(1)可以得出不同应力下2D-C/SiC材料的卸载残余应变,如图6所示。可以看出,外加应力不大于100MPa时,预测值与试验值比较吻合,载荷大于150MPa时,预测值与试样T2和T4的试验值较为接近,而试样T2和T4的断口位于引伸计的刀口之间(图5)。这说明,大的裂纹张开位移在2D-C/SiC材料中一般出现在将会断裂的损伤区域,当裂纹张开位移超过某一临界值时,裂纹将会发生失稳扩展进而导致材料断裂。另外,式(1)没有考虑卸载过程中界面的逆滑移,导致模拟结果在载荷大于200MPa时误差较大。
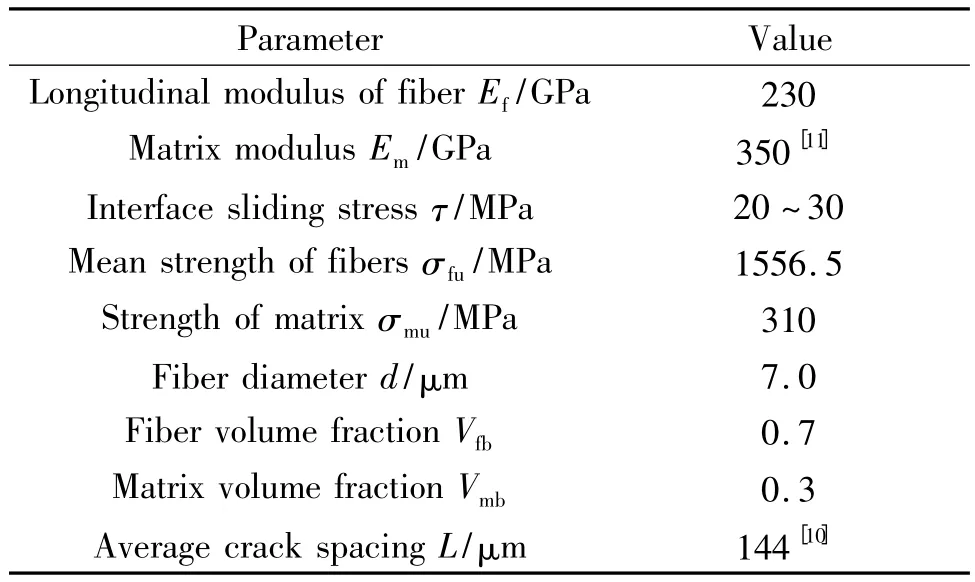
表2 材料弹性常数及参量Table 2 Parameters of the material

图6 残余应变的试验值和模拟曲线Fig.6 Experimental and simulated data for residual strain of 2D-C/SiC composites
在忽略90°层的承载能力的条件下,根据式(8)给出的卸载模量与试验值吻合较好,如图7所示。材料的卸载模量和拉伸应力的关系既可以通过试验数据进行拟合,也可以通过式(9)进行计算。对于试样T1,若根据式(3)进行数据拟合,可以得出参数A= - 0.612,B=1.16 × 10-3;若根据式(7)进行拟合,则可以得出 a=6.09×10-3,b=0.03×10-3。模型给出的应力-应变预测曲线如图8所示,可见在不大于100MPa的情况下吻合较好,当载荷较大时偏差较大,其有多方面原因:(1)在断裂区以外,材料损伤程度较轻,因此90°层对于材料的整体刚度有贡献;(2)虽然假定界面剪切应力较大,但是在卸载过程中,界面仍然应该会产生反向滑移;(3)基体裂纹演化过程的影响。这种情况下,模型预测曲线更接近试样T2和T4的试验应力-应变曲线。
需要指出的是,应用式(6)计算材料的卸载模量时,η的取值范围是0≤η≤1,因为纵向纤维束的最小卸载模量应该是EfVf。这预示着,当界面结合较弱时,模型给出的应力-应变曲线在载荷较大时会出现另外一个拐点。

5 强度分析
拉伸试验表明,2D-C/SiC复合材料断裂时,纤维束断裂拔出较长,束内有明显的单纤维拔出,材料发生的是准脆性断裂。忽略90°层的承载能力,建立图9所示的细观力学模型,其中L为裂纹间距,m为界面脱粘长度。当0≤x≤m时,纤维应力可以表示为:式中,S为裂纹面上的纤维应力,载荷均匀分担条件下时根据最大应力判据,当S=σfu时,纤维断裂失效,其中σfu为纤维的就位强度。在界面全部脱粘的条件下,材料断裂时纤维所承担的平均应力为:

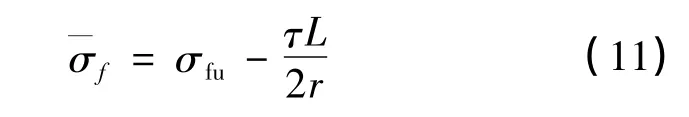
于是根据混合率得出2D-C/SiC复合材料的拉伸强度表达式为:
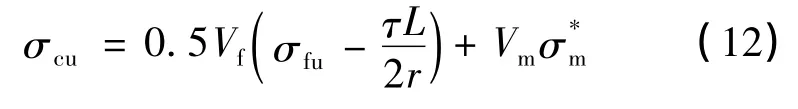
上式中,σ*m为材料断裂时基体所承受的应力,其计算公式为:

其中,σmu为基体强度,φc为基体承载面积减缩率,取值为0.2。
文献[5]通过试验测得涂层厚度约为0.8μm的纤维,其就位强度为674MPa。根据文献[4]的研究结论,可以得到T300纤维的强度与涂层厚度α的关系表达式为:

2D-C/SiC复合材料中,纤维的涂层厚度为0.15~0.2μm,根据上式可以得出纤维的就位强度范围是1348 ~1556.5 MPa。
根据式(5)得出界面全部脱粘的理论载荷为237MPa,从表1可以看出,除了试样L3,其他试样的最终载荷均大于237MPa,因此,公式(12)是适用的。模型给出的拉伸极限强度范围是237.97~279.67 MPa,与试验值吻合,表明90°层中纤维对于材料强度的贡献可以忽略。
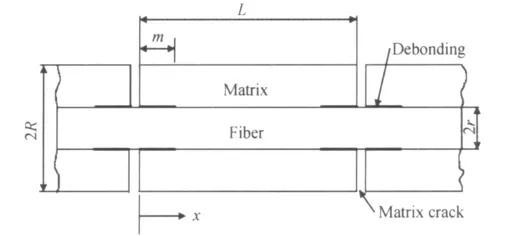
图9 细观力学分析模型Fig.9 Micromechanics based analysis model
6 结论
(1)2D-C/SiC复合材料的单轴拉伸行为具有明显的非线性,最终发生准脆性断裂。循环加卸载过程中,材料产生较大残余应变,卸载模量显著下降。
(2)基于细观力学建立的损伤本构模型能较好模拟材料的拉伸应力-应变行为。分析计算表明,残余应变和裂纹间距、裂纹张开位移有关;卸载模量同样和裂纹间距有关,还和界面脱粘长度,即界面脱粘率相关。
(3)2D-C/SiC复合材料的拉伸行为主要由纵向纤维束控制,横向纤维束对于整体刚度和强度贡献较小。
(4)基于简单剪滞理论建立的强度模型能较好预测2D-C/SiC复合材料的拉伸强度。计算表明,对于纤维涂层厚度为0.15~0.2μm的材料,其强度范围是237.97~279.67 MPa。
[1]ZHU S,MIZUNO M,KAGAWA Y,et al.Monotonic tension,fatigue and creep behavior of SiC-fiber-reinforced SiC-matrix composites:a review[J].Composites Science and Technology,1999,59:833-851.
[2]GREGORY N,MORSCHE R.Stress-dependent matrix cracking in 2D woven SiC-fiber reinforced melt-infiltrated SiC matrix composites[J].Composites Science and Technology,2004,64:1311-1319.
[3]CARRERE N,MARTIN E,LAMON J.The influence of the interphase and associated interfaces on the deflection of matrix cracks in ceramic matrix composites[J].Composites:Part A,2000,31:1179-1190.
[4]THOMAS H,HERWIG P,KARL K.Coating of carbon fibers——The strength of the fibers[J].J Am Ceram Soc,1995,78:133-136.
[5]王波.三维编织复合材料力学行为研究[D].西安:西北工业大学工程力学系,2004,34-36.
[6]罗国清.3D-C/SiC复合材料的拉伸性能[D].西安:西北工业大学,2003,30.
[7]管国阳,矫桂琼,张增光.2D-C/SiC复合材料的宏观拉压特性和失效模式[J].复合材料学报,2005,22(4):81-85.
[8]SOLTI J P,MALL S,ROBERTSON D D.Modeling damage in unidirectional ceramic matrix composites[J].Composites Science and Technology,1995,54:55-66.
[9]梅辉,成来飞,张立同,等.2维C/SiC复合材料的拉伸损伤演变过程和微观结构特征[J].硅酸盐学报,2007,35(2):137-143.
[10]张钧,徐永东,张立同,等.3D C/SiC复合材料基体裂纹间距分布规律[J].航空材料学报,2003,23(3):11-14.
[11]MEI H,CHENG L F,ZHANG L T,et al.Modeling the effects of thermal and mechanical load cycling on a C/SiC composite in oxygen/argon mixtures[J].Carbon,2007,45:2195-2204.
[12]HSUEH C H.Crack-wake interfacial debonding criteria for fiber-reinforced ceramic composites[J].Acta Mater,1996,44(6):2211-2216.
[13]杨成鹏,矫桂琼,王波,等.2D-C/SiC复合材料的氧化损伤及刚度模型[J].复合材料学报,2009,26(3):175-181.
[14]EVANS A G,DOMERGUE J M,VAGAGGINI E.Methodology for relating the tensile constitutive behavior of ceramic-matrix composites to constituent properties[J].Journal of the American Ceramic Society,1997,77(6):1425-1435.

