Li2部分电子态的完全振动能谱与离解能的精确研究*

樊群超孙卫国†李会东冯灏

1)(西华大学物理与化学学院，先进计算研究中心，成都610039)

2)(四川大学原子和分子物理研究所，成都610065)

(2009年11月23日收到;2010年1月30日收到修改稿)

Li2部分电子态的完全振动能谱与离解能的精确研究*

樊群超1)孙卫国1)2)†李会东2)冯灏1)

1)(西华大学物理与化学学院，先进计算研究中心，成都610039)

2)(四川大学原子和分子物理研究所，成都610065)

(2009年11月23日收到;2010年1月30日收到修改稿)

本文将孙卫国等建立的精确计算双原子分子离解能的解析表达式作为分子振动能级正确收敛的重要物理判据，应用代数方法，进一步研究了重要的碱金属Li2的5个电子态的完全振动能谱和离解能，获得了这些电子态的精确振动光谱常数，同时也得到了包括接近分子离解极限在内的完全振动能谱和与实验值符合得很好的理论离解能.这些计算结果为许多需要这些电子态振动数据的研究领域提供了重要的研究数据.

代数方法，Li2，振动能级，离解能

PACC:3310，3520P

1. 引言

碱金属Li2由于其简单的电子结构，成为实验和理论上用来研究中性同核双原子分子之间相互作用的典型分子.几十年来，国际上对Li2的分子结构、势能函数、振动-转动光谱性质以及各电子态的离解能进行了大量的理论和实验研究［1—9］，并不断取得新的进展.理论上，人们对Li2的振转能级以及部分电子态的研究主要基于从头计算方法［1—4］，直到1999年，Linton等［4］才首次应用近离解极限展开技术(near dissociation energy expansion，简称NDE)对Li2的a3Σ+u电子态的低激发振动谱项值进行了研究，并确定了该电子态的离解能.建立这些理论方法，往往需要考虑体系的多组态函数以及电子相关效应，根据经验选择基函数的集合以及很多的变分参数，然后经过复杂的计算和合理的修正，最后才能够得到收敛的计算结果.然而，要获得体系正确的基函数集合和变分参数却是非常困难.由于这些理论方法存在其自身的局限性，因此对于大多数电子态，最终很难从理论上获得高激发振动光谱和离解能的正确数据.

实验上，对Li2电子态振动能级和离解能的研究方法主要有微扰光学双共振光谱法(perturbation facilitatedopticalopticaldoubleresonance spectroscopy，简称PFOODR)［10，11］和激光诱导荧光傅里叶变换光谱法(laser induced fluorescence fourier transform spectrometry，简称LIFFTS)［12］.然而，对于大多数电子态而言，当分子处于高激发振动态尤其是处于分子离解极限附近的时候，由于分子振动能级的间隔非常小而且密，从而对实验仪器的精度要求很高，使得很难获得此刻的正确振动能级.因此在实验上利用这些方法一般只能观测到分子处于低激发态的一些振动能级，而所获得的分子离解能大多是通过拟合势能曲线、外推法来得到的数据［7］.目前，已发表的文献中对于有关Li2长程分子作用势、离解能和精确的高激发态振动能级的数据还比较缺乏.因此，我们仍然很有必要对Li2各电子态的完全振动能谱及离解能进行进一步的研究.

本文应用孙卫国等［13—16］建立的精确计算分子完全振动能谱代数方法(AM)，从精确的实验能级或量子理论振动能级出发，通过严格求解能级与光谱常数的正确代数关系式，避开了繁琐的势能函数和薛定谔方程求解过程，获得了7Li2的a3Σu+，33Σg+，13Δg，b3Πu和6Li2的11Πg等5个电子态的精确振动光谱常数和完全振动能谱，同时应用孙卫国等［17，18］最近建立的计算精确的分子离解能的新解析表达式，计算了以上5个电子态的理论离解能DAeM，获得了十分精确的结果.

2. 理论与方法

在前一阶段的工作中，我们总结了LeRoy和Bernstein［19，20］研究分子离解能的理论工作，在他们的工作基础上，对于一个稳定的双原子分子或离子电子态，我们获得了计算这些电子态离解能的新公式［17，18］

若(2)式不满足，则说明用于计算离解能Dceal的三个最高振动能级含有不可忽略的误差.

为了获得双原子分子精确的完全振动能谱，孙卫国等［13—16］用二阶微扰理论得到了非相对论核运动振动能级的解析展开表达式，即

AM［13—16］的基本出发点是将(3)式改写成矩阵形式

其中振动光谱常数的向量矩阵X和振动能量矩阵E分别表示为

AM方法基于这样的物理事实:对于绝大多数双原子分子的稳定电子态，现代实验技术和量子理论往往难以获得高振动激发态尤其是接近离解极限区域的振动能级，总可以获得各电子态的一部分量子态不太高的振动能级的精确数据子集合［Eν］.而这些精确的实验数据基本上包含了所有重要分子振动信息和所有重要的微观量子效应，如电子-电子相关、自旋-轨道耦合、电磁效应等等.因此，用AM方法在数学和物理上不加近似地从这些精确实验能级子集合萃取出一组包含了所有重要的高阶非谐性效应和分子振动信息的振动光谱常数X，再将这组常数代入振动能级的正确表达式(3)式，即可得到某电子态的真实振动完全能谱的一个正确表象{Eν}.所以，基于有限的精确实验数据和严格的微扰理论表达式(3)所获得的这个振动能级的完全集合{Eν}不仅能精确地重复已知实验能级子集合［Eν］，而且能正确地获得该电子态所有高激发振动量子态的能级.而这些能级往往是实验上很难得到的.应用AM方法于双原子分子的电子态时，可以从由m个已知实验能级组成的能级子集合［Eν］中选取N个小能级组，每组8个能级，然后解方程(3)N次，并获得N组振动光谱常数X′s.这N组常数中，总有一组常数X能最好地满足下列要求:

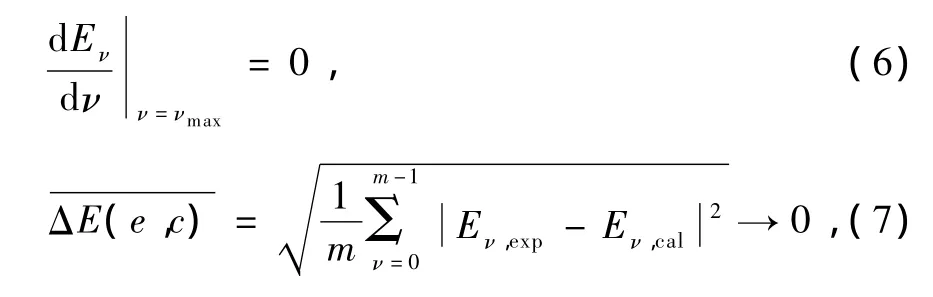
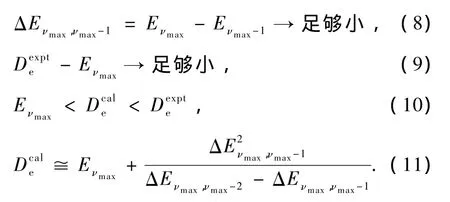
那么这组振动光谱常数就是该分子体系真实振动光谱常数集合的最佳物理表象之一，从而由此计算的振动能谱就是包含该体系所有真实振动能级的一组完全振动能谱{Eν}.(11)式即计算离解能的新公式(1)式，由于该式要求使用三个精确的最高振动能级，所以(1)式又可用作双原子体系的完全振动能谱是否很好收敛的一个重要物理判据.

3. 应用与讨论

本文应用AM方法分别计算了7Li2的a3Σu+，33Σg+，13Δg，b3Πu和6Li2的11Πg等5个电子态的精确振动光谱常数和完全振动能谱，再根据这些电子态的正确物理能级，利用(1)式分别获得了它们的理论离解能Dcale.表1列出了上述5个电子态的分别从文献中获得的和AM方法得到的振动光谱常数(ω0，ωe0，ωe，ωexe，ωeye，ωeze，ωete，ωese，ωere).这些电子态的实验振动能谱和AM振动能谱以及离解能的数据分别列于表2中.

表1很清晰地显示出，由AM方法得到的谐振常数ωe与相应电子态的文献值符合得非常好.就多数电子态而言，由AM方法得到的非谐振常数ωexe与文献值符合得也比较好;而文献中给出的实验振动光谱常数还比较缺乏，尤其是高阶振动光谱常数的数据，其主要原因之一是文献在使用类似方程(3)的振动能级展开表达式中截取的项比较少.例如，实验上在对7Li2的33Σ+［23］电子态进行研究时只取到了3阶，所以其误差较大，因此如果用仅有的这些低阶振动光谱常数去计算这些电子态的全部振动能量，则得到的完全振动能谱尤其是高激发振动态的能谱数据将含有很大的误差，而由AM振动光谱常数计算得到的最高振动能量与实验离解能Dexptge非常接近，这表明由AM方法得到的振动光谱常数比文献值精确得多.

表1 用AM方法和从文献中分别得到的Li2部分电子态的振动光谱常数(单位:cm－1)

将表2所列的各电子态的AM能谱与文献给出的实验能级相比较可知，AM能谱的精确度完全取决于实验能级的精确度，只要实验能级精确可靠，则AM将产生一组十分准确的光谱常数，由此计算而得到的AM振动能谱将必然很好地再现实验能谱并正确地产生包括最高振动能级在内的全部高阶振动能级，从而获得离解能的准确度也应该是相当高的.在表2中7Li2的a3Σ+u电子态，在实验上Linton［4］小组获得了11个振动能级，最高振动能级E(νmax=10)=333.2690cm－1，这个值和实验值Dexpt=333.690cm－1非常接近，说明实验数据是正e确可靠的，因此用AM方法同样也得到了11个振动能谱，我们可以断定该电子态的完全振动能谱只有11个，分别将最高三个精确的实验能级和AM振动能级代入新公式(1)计算得到的离解能分别为DAexMpt=333.6557cm－1和DAeM=333.2904cm－1，这些结果和Deexpt相比，误差都非常小.

表2给出了所列各电子态的AM完全振动能谱

{Eν}，对这些电子态而言，所有AM振动能谱都满足判据条件(6)—(11)式，因此用AM方法获得的振动能谱是体系正确的完全振动能谱.这些振动能谱都是使用AM方法，利用各电子态的已知实验能级子集合［Eν］求解方程(3)而不用任何数学近似和物理模型而得到的(所选8个振动能级均以黑体标出).因此这些电子态的振动光谱常数、振动能谱不仅能很好地重复已知实验能级或RKR(Rydberg-Klein-Rees)数据，而且能够合理地产生实验难以得到的所有高激发态振动能级，从而获得非常接近于离解极限的最高振动能级和最大振动量子数νmax.比较典型的例子是表2中7Li2的电子激发态b3Πu，Linton课题组［24］于1990年从实验中对该电子态仅获得28个振动能级，即最高振动能级E(νmax=27) =7984.1370cm－1，这个值远小于离解能的实验值=12178.9050cm－1，而用AM方法得到该电子态的完全振动能谱{Eν}的能级数为62个，最高振动能级EAM(νmax=61)=12178.6680cm－1，将最高三个AM振动能谱代入新公式(1)计算得到的离解能为DAeM=12178.8763cm－1，此值和Deexpt相比，误差仅为0.0287cm－1，可见获得的AM数据是正确可靠的.

表2 Li2部分电子态的AM振动能谱和文献发表的振动能量值(单位:cm－1)

续表2

4. 结论

对碱金属Li2的很多电子态而言，其完全振动光谱特别是高振动激发能级还非常缺乏，而且无论是实验上还是利用理论方法也很难获得这些重要的振动信息.本文从实验上获得的各电子态的部分已知精确实验能级出发，应用精确研究双原子分子离子的完全振动能谱的代数方法(AM)，结合基于LeRoy和Bernstein［19，20］研究分子离解能的理论基础而建立的计算分子离解能的新公式，通过严格求解代数方程，获得了7Li2的a3Σu+，33Σg+，13Δg，b3Πu和6Li2的11Πg等5个电子态的精确振动光谱常数、完全振动能谱和理论离解能，从而为那些需要Li2高振动激发态的精确能级的研究工作提供了重要的研究数据.

［1］Konowalow D D，Fish J L 1983 Chem.Phys.77 435

［2］Schmidt-Mink I，Müller W，Meyer W 1985 Chem.Phys.92 263

［3］Poteau R，Spiegelmann F 1995 J.Mol.Spectrosc.171 299

［4］Linton C，MartinF，RossAJ，RussierI，CrozetP，Yiannopoulou A，Li L，Lyyra A M 1999 J.Mol.Spectrosc.196 20

［5］Cacciani P，Kokoouline V，Bouloufa N，Masnou-Seeuws F，Vetter R 2003 Phys.Rev.A 68 042506

［6］Peng Q，Lazarov G，Lyyra A M，Jeung G H 2008 J.Mol. Spectrosc.247 184

［7］Li D，Xie F，Li L，Lazoudis A，Lyyra A M 2007 J.Mol. Spectrosc.246 180

［8］Coxon J A，Melville T C 2006 J.Mol.Spectrosc.246 235

［9］Yan T M，Han Y C，Yuan K J，Cong S L 2008 Chem.Phys. 348 39

［10］Russier I，Yiannopoulou A，Crozet P，Ross A J，Martin F，Linton C 1997 J.Mol.Spectrosc.184 129

［11］Lazarov G，Lyyra A M，Li L 1997 J.Mol.Spectrosc.205 73

［12］Barakat B，Bacis R，Carrot F，Churassy S，Crozet P，Martin F 1986 J.Chem.Phys.102 215

［13］Sun W G，Hou S L，Feng H 2002 J.Mol.Spectrosc.215 93

［14］Sun W G，Ren W Y，Hou S L 2005 Mol.Phys.103 2335

［15］Sun W G，Liu X Y，Wang Y J，Zhan Y，Fan Q C 2007 Prog. Phys.27 151(in Chinese)［孙卫国、刘秀英、王宇杰、詹妍、樊群超2007物理学进展27 151］

［16］Ren W Y，Sun W G 2005 Acta Phys.Sin.54 594(in Chinese)［任维义、孙卫国2005物理学报54 594］

［17］Sun W G，Fan Q C，Ren W Y 2007 Sci.Chin.Ser.G 50 611

［18］Fan Q C，Sun W G 2009 Spectrochi.Acta Part A 72 298

［19］LeRoy R J，Bernstein R B 1970 J.Chem.Phys.52 3869

［20］LeRoy R J，Bernstein R B 1971 J.Mol.Spectrosc.37 109

［21］Linton C，Murphy T L，Martin F，Bacis R，Verges J 1989 J. Chem.Phys.91 6036

［22］Linton C，Martin F，Bacis R，Verges J 1990 J.Mol.Spectrosc. 142 340

［23］Yiannopoulou A，Urbanski K，Lyyra A M，Li L，Ji B，Bahns J T，Stwalley W C 1995 J.Chem.Phys.102 3024

［24］Russier I，Yiannopoulou A，Crozet P，Ross A J，Martin F，Linton C 1997 J.Mol.Spectrosc.184 129

［25］Xie X，Field R W 1986 J.Mol.Spectrosc.117 228

［26］Kaldor U 1990 Chem.Phys.140 1

PACC:3310，3520P

*Project supported by the National Natural Science Foundation of China(Grant No.10774105)，the Youth Fund of the Education Department of Sichuan Province，China(Grant No.09ZB083)，and the Research Fund of the Key Discipline of Atomic and Molecular Physics，Xihua University，China.

†Corresponding author.E-mail:weiguosun@x263.net

The full vibrational spectra and dissociation energies of Li2molecule*

Fan Qun-Chao1)Sun Wei-Guo1)2)†Li Hui-Dong2)Feng Hao1)
1)(Research Center for Advanced Computation，School of Physics and Chemistry，Xihua University，Chengdu610039，China)
2)(Institute of Atomic and Molecular Physics，Sichuan University，Chengdu610065，China)
(Received 23 November 2009;revised manuscript received 30 January 2010)

Based on the algebraic method(AM)proposed to calculate accurate full vibrational energies for diatomic molecules in Sun’s previous work，the parameter-free analytical formula for dissociation energy of diatomic system is used to study the dissociation energies and the full vibrational spectra of 5 electronic states of Li2molecule in this work.The results show that the AM vibrational spectra and dissociation energies are in excellent agreement with experimental results.

algebraic method，Li2，vibrational energy，dissociation energy

book=353,ebook=353

*国家自然科学基金(批准号:10774105)、四川省教育厅青年基金(批准号:09ZB083)和西华大学原子与分子物理重点学科基金资助的课题.

†通讯联系人.E-mail:weiguosun@x263.net