双层反铁磁体K3Cu2F7中轨道序驱动的自旋二聚化*
陈东猛刘大勇
1)(中国石油大学(华东)物理科学与技术学院,东营257061)
2)(中国科学院固体物理研究所材料物理重点实验室,合肥230031)
(2010年3月9日收到;2010年3月29日收到修改稿)
双层反铁磁体K3Cu2F7中轨道序驱动的自旋二聚化*
陈东猛1)†刘大勇2)
1)(中国石油大学(华东)物理科学与技术学院,东营257061)
2)(中国科学院固体物理研究所材料物理重点实验室,合肥230031)
(2010年3月9日收到;2010年3月29日收到修改稿)
基于自旋-轨道-晶格Hamilton量,应用团簇自洽场方法,研究了双层钙钛矿结构材料K3Cu2F7基态的晶格、磁及轨道结构,发现近孤立的双层的对称破缺和Jahn-Teller晶格畸变使得Cu2+离子在每层内交替占据轨道,进而导致双层的层间表现为强的反铁磁耦合,层内为弱的铁磁耦合.强反铁磁耦合导致层间自旋二聚化,形成自旋单重态.层内Cu2+离子的轨道占据与弱的铁磁耦合满足Goodenough-Kanamori-Anderson规则,因此自旋间并无磁阻挫作用,利于形成稳定的自旋二聚化态.由键算符平均场方法得到自旋单重态-三重态激发能隙约为326 K,与实验值400K相比略小.该理论也适用于同类晶格结构材料Cs3Cu2Cl4Br3自旋二聚态的形成.
自旋二聚化,轨道序,双层反铁磁体K3Cu2F7
PACC:7510J,7530E,7550E
1. 引言
近年来,丰富的场致量子相的出现使得二聚化的量子反铁磁体引起了广泛的关注.在无外场时,这类体系中自旋S=1/2的化合物其基态为自旋单重态基态,也称为自旋二聚态(spin dimer state),即态中每一个自旋都与其某一最近邻自旋形成自旋单重态.体系自旋二聚态与自旋三重态激发态(spin-triplet excited state)间存在自旋能隙,在足够强的磁场下许多材料中观察到了自旋单重态-三重态激发磁子的Bose-Einstein凝聚[1—3].除自旋自由度外,某些过渡金属氧化物中还具有轨道自由度[4].相比自旋系统中磁各向异性相互作用及磁阻挫作用是形成自旋二聚态的主要原因,如文献[5—9],具有轨道自由度的过渡金属氧化物中轨道通过特殊的有序排列可调整自旋间互作用的强度,从而利于形成自旋单重态基态.因此,人们开始对具有轨道自由度的这类体系进行研究[10—14].
最近磁化率实验表明,类Sr3Ti2O7结构的单晶双层钙钛矿型化合物CsCuClBr[13]和3243K3Cu2F7[14]自旋具有明显的二聚化特征.以这类材料中的K3Cu2F7为例,CuF6八面体中心的Cu2+离子3d9配置,其中t2g轨道填满,而简并的双eg轨道被一个空穴占据.CuF6八面体角间相连形成平行于c轴的双层正方格子结构,所有双层都是等价的并且近邻的双层间错位(a+b+c)/2.在低温下的Jahn-Teller效应使得CuF6八面体间发生相合作的畸变,八面体在ab平面沿a轴和b轴交替伸长,而沿c轴八面体压缩,这类似于KCuF3的Jahn-Teller畸变.沿c轴的压缩,使得每个Cu2+离子的空穴利于占据双层中沿c轴相对位置上的Cu2+离子空穴的轨道的交叠较大,使得空穴的自旋间易于形成强的反铁磁关联,从而易于形成沿c轴两空穴自旋间的自旋单重态.结构分析及磁化率实验支持材料基态为自旋二聚态,并推得Cs3Cu2Cl4Br3和K3Cu2F7自旋能隙分别约为2000和400K,这远大于如Sr3Cr2O8[15]等材料的自旋能隙.这类材料的自旋二聚态及自旋能隙的成因还没有理论上的报道.
本文以K3Cu2F7为例,描述了一种在双层钙钛矿结构的过渡金属氧化物中形成稳定自旋二聚态的微观理论.指出近孤立的双层的对称破缺和Jahn-Teller晶格畸变使得Cu2+离子在ab面内以或轨道占据,并且两轨道有序交替排列.这种轨道序稳定了材料的自旋二聚态.计算结果表明纯的超交换作用可以得到稳定的自旋二聚化基态,而Jahn-Teller效应起到了稳定和调节轨道占据的作用.自旋单重态-三重态激发能隙约326 K,与实验值400K比较接近.
2. 模型Hamilton量及团簇自洽场方法
类似K2CuF[16]4,双层钙钛矿结构的K3Cu2F7近邻的双层间平移[1/2,1/2,1/2],导致两个双层间的耦合也很弱,因此每个双层是近孤立的.为简化模型仅考虑K3Cu2F7单个双层,其有效Hamilton量可以分为以下两部分:
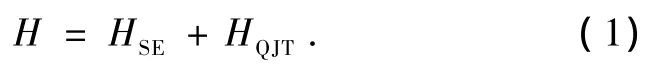
第一项HSE代表两最近邻的Cu2+离子eg空穴间的超交换作用,可由双eg轨道简并的Hubbard模型的二阶微扰近似得到[17].其形式为

其中si代表i位置的自旋算符.算符Iαi满足Iαi= cos(2πmα/3)τzi-sin(2πmα/3)τx,指标α代表坐标轴,α=x,y和z,分别对应晶体a,b和c轴,而(mx,my,mz)=(1,2,3).τ为轨道赝自旋算符,满足τ= (1/2)Σabca+σabcb,式中ca+为在a轨道产生一个空穴,而σ为Pauli矩阵.τzi=1/2,-1/2分别代表空穴完全占据或轨道.常数J1,J2, J3和J4为超交换耦合强度,满足

其中U和U1分别代表轨道内和轨道间两空穴的Coulomb作用,JH为Cu2+离子的3d空穴间的Hund耦合.参照KCuF3,由于Cu2+离子的3d轨道和F-离子的2p轨道间的pd杂化效应[18],选取U=U1+ JH.并且采用KCuF3的LDA的计算结果,取U=7.5 eV,JH=0.9 eV[19].沿着z方向的双层内两层间的跃迁积分t3z2-r2,3z2-r2=4t最大,取t=0.12 eV,这样超交换的能量尺度为J=16t2/U=30.7 meV.
第二项相应于每个Cu2+离子空穴的Jahn-Teller效应项,表示为
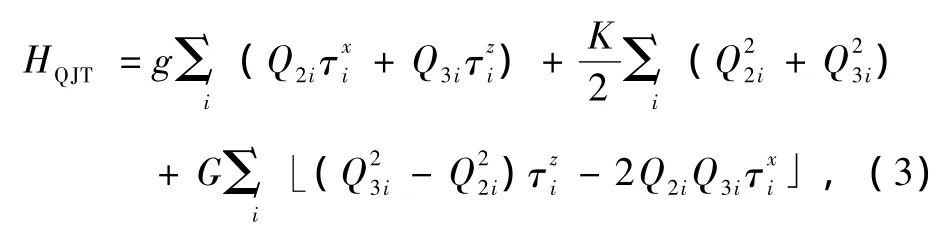
(3)式中前两项对应Jahn-Teller效应的线性谐振,而第三项对应非简谐效应,这种非简谐效应贡献于体系的各向异性能[20].g为线性Jahn-Teller耦合强度,K为弹性常数,G是非简谐耦合系数.Q2i和Q3i是振动的两种简正模式,分别定义为

其中X,Y和Z是第i个F-离子的坐标[21].对K3Cu2F7,全文中都采用K=10 eV/2.
同时处理包含自旋、轨道和晶格间相互作用的Hamilton量即(1)式是非常困难的.最近发展的团簇自洽场方法[22,23]结合了团簇中电子间的量子涨落效应和环境对团簇的自洽场影响,是求解多自由度系统基态的有效方法.团簇自洽场的基本思想为:首先,按照Feynman-Hellman定理,利用基态能对Q2i和Q3i取变分极值即和,将Q2i和Q3i变为轨道极化强度的函数,这样通过自洽Q2i和Q3i使基态能最小的方式将Hamilton量简化为自旋和轨道两自由度的相互作用项;接着利用精确对角化对团簇及其自洽场自洽处理得到基态,进而就可以研究基态的自旋和轨道的配置以及相应的磁和轨道性质.该方法的详细描述,参见文献[23,24].考虑到K3Cu2F7单个双层结构的对称性,所取团簇如图1所示.对KCuF3可视为K3Cu2F7的双层结构沿z轴平移得到.由于我们忽略双层与双层间的耦合而仅考虑近孤立的单个双层结构,因此对K3Cu2F7沿z轴方向双层结构晶格平移对称性破缺,导致其自洽场与KCuF3不同[25].
3. 计算结果和讨论
基于Hamilton量利用团簇自洽场方法的计算结果,研究零温下K3Cu2F7的基态.首先分析基态下的晶格结构、磁结构和相应的轨道占据,接着研究体系基态的自旋单重态-三重态激发能隙.
3.1. 基态的晶格、磁和轨道结构
3.1.1. 晶格构型
利用团簇自洽场方法自洽求得的Q2和Q3的分布来研究K3Cu2F7的晶格构型,发现在xy面的畸变具有两种构型A:和B:的形式,其中A和B相应于团簇中两相邻的Jahn-Teller畸变中心,并交替出现.即在ab面内CuF6八面体沿x轴和y轴交替伸长.而xy面间CuF6八面体沿z轴畸变方式呈铁型或反铁型排列,并且两种排列方式下能量简并.类似于KCuF3,将对应的晶体结构分别称为d型和a型结构.此时,G为正值,类似于KCuF3[25]和4d9材料Cs2AgF4[24].实验中观察到了xy面中CuF6八面体的交替伸长,而xy面间CuF6八面体间畸变方式的排列还需进一步精细实验的验证.
图2中给出了Q2和Q3对不同的Jahn-Teller线性耦合强度g和非简谐耦合强G的变化关系.可以发现随着Jahn-Teller耦合强度g和G的增加,电子晶格耦合增强导致Jahn-Teller畸变的幅度Q2和Q3增加.Q3<0意味着CuF6八面体中沿z轴Cu—F键压缩,而z轴压缩的CuF6八面体将使得Cu2+空穴倾向于占据能量低的轨道.由实验晶格参数[26]推得和Q3=-0.151.理论上,在g=4.0 eV和G=0.75g时得到0.247和Q3=-0.143,同KCuF3类似,团簇自洽场方法的计算值比实验值略小.
3.1.2. 自旋二聚态及轨道占据

图2 晶格畸变幅度Q2i和Q3i随线性Jahn-Teller耦合强度g和不同非简谐耦合强度G的依赖关系
对于KCuF3,其超交换作用中轨道部分沿x,y和z轴方向各向同性,并且轨道间的相互作用具有很强的阻挫特征,因此KCuF3中电子超交换作用的基态为包含多重简并态的自旋轨道液体态[25].然而,双层结构的K3Cu2F7,由于忽略双层与双层间弱的耦合作用而仅考虑单个双层结构,沿z轴方向的晶格平移对称性破缺,使得原本在KCuF3基态中的多重简并的态部分解除简并.团簇自洽场方法计算表明,超交换作用下系统的轨道在xy面内呈现反铁型排列,在两层间轨道的排列与Jahn-Teller晶格畸变的方式相对应:对a型结构为反铁型排列,而对d型结构为铁型排列,如表1中轨道关联函数所示,也即对应a型晶格结构轨道为G型轨道序,而对应d型晶格结构轨道为C型轨道序.两轨道晶格中轨道占据满足,相比于轨道中成分略多.这种轨道占据导致沿z方向双层中相对的两自旋间具有强的反铁磁关联,自旋关联函数〈sisi+z〉=-0.749,即此时沿z轴方向的两层中相对的两空穴自旋间已形成自旋单重态.在xy面内的自旋间为弱铁磁耦合(见表1自旋关联函数),与轨道间的反铁型耦合相对应,这符合自旋轨道排列的Goodenough-Kanamori-Anderson(GKA)规则[27],减少了自旋及轨道间的量子涨落.沿z方向的相对的两空穴的轨道中轨道占主要成分,使得轨道交叠较大,从而利于两自旋间形成近孤立的自旋单重态;xy面中轨道间的弱的反铁型轨道排列,使得自旋二聚态间具有弱的铁磁耦合,从而形成自旋二聚态.因此,空穴特殊的轨道有序排列,是自旋二聚态形成的重要原因.

表1 超交换作用(SE)及超交换和Jahn-Teller效应共同作用(SE+JT)下的自旋极化强度、自旋耦合强度、轨道极化强度及轨道和自旋的关联强度
在存在超交换作用的基础上,进一步研究了Jahn-Teller效应对自旋和轨道结构的影响.从Jahn-Teller效应Hamilton量(3)式来看,晶格与轨道的相互作用使晶格产生了影响轨道占据的“轨道场”. Hamilton量中τx部分轨道场导致和两轨道的占据概率趋同,τz部分轨道场则导致轨道极化(τz=1/2)或轨道极化(τz=-1/2).对线性Jahn-Teller晶格-轨道耦合作用,因为g>0并且Q3<0,因此导致〉占据概率增大.对比超交换作用,由于单独的线性Jahn-Teller效应项下轨道占据概率大于纯超交换作用的结果,因此轨道占据〈τz〉随着线性作用强度g增大而增加,如图3(b)所示.而当g>2.0 eV/轨道占据趋于常数,这主要是因为此时线性Jahn-Teller效应在轨道占据中占主导作用,并且从图2看到此时趋于常数,因此导致轨道占据不再随g增加,从而〈τz〉趋于常数.然而,按照孤立空穴的轨道占据下〈τx〉与〈τz〉互补来考虑,〈τx〉随g的变化比较特殊.可能的原因是:超交换作用下,仍有较强的轨道阻挫效应[25],导致轨道量子涨落,轨道的极化强度不再满足类孤立空穴的互补关系〈τz+τx〉=0.5. Jahn-Teller晶格-轨道作用提供的轨道场减少了轨道的阻挫,因此虽然起始时轨道极化强度〈τx〉随着g增加而增加,但随g增大,Jahn-Teller互作用项在轨道占据中逐渐起主导作用,而对线性Jahn-Teller项轨道占据概率大于纯超交换作用的结果,必然导致随g增大〈τx〉减小.同〈τz〉类似,当Jahn-Teller起主导作用时,〈τx〉也趋于常数.因为非简谐Jahn-Teller效应作用项下,轨道占据概率小于超交换作用下的占据概率,使得非简谐项的加入导致轨道占据〈τz〉随着非简谐作用强度G增大而减少,而相应的〈τx〉则增大,如图3所示.
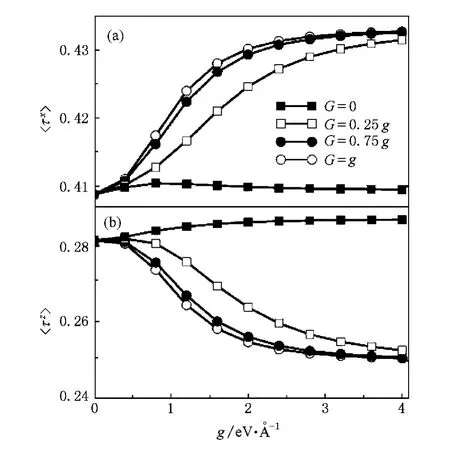
图3 轨道极化强度(a)〈τx〉和(b)〈τz〉随线性Jahn-Teller耦合强度g和不同非简谐耦合强度G的变化关系
为研究自旋关联对Jahn-Teller效应的响应,定义沿α轴的自旋耦合强度为

从图4可以看到,Jahn-Teller作用并没有改变系统的磁结构:平面内为弱铁磁耦合,在两层间为强的反铁磁耦合,即基态仍然保持自旋二聚态的特征.非简谐Jahn-Teller效应下,轨道占据概率下降,导致沿z轴两层间的空穴轨道交叠减弱,因此自旋耦合强度Jz随G增大而减少,这与图5中自旋关联〈sisi+z〉随G增加而减少相对应.同时相应的轨道占据概率的增加,使得在xy面内沿x和y轴电子间的轨道交叠增大,因此Jx,y随G增大而增大,而〈sisi+x〉也随G增大而增大.只考虑线性Jahn-Teller效应时,随耦合强度g的增加,导致占据率增加.那么,按照GKA规则,Jz将增加,相应的Jx,y将减少,而实际自旋耦合强度的变化却恰好相反.这主要是超交换作用下,空穴间的关联较强,而Jahn-Teller效应的加入增加了轨道场对轨道量子涨落的限制,从而减少了电子间的关联,因此自旋耦合强度Jz减少,相应的Jx,y增加.尽管随Jahn-Teller耦合强度的增强而减弱,但始终保持了沿z方向的自旋耦合Jz远大于Jx,y,即自旋具有很强的各向异性特征,如图4所示.这也反映在沿z轴的反铁磁自旋关联〈sisi+z〉≈-0.75,始终保持了二聚态的特征,如图5所示.从表1中可见,当g=4.0 eV和G=0.75g时,自旋和轨道的结构不变,并且此时每个Cu2+离子轨道交替占据

图4 沿x,y和z方向的自旋耦合强度Jx,y和Jz以及它们的比值随线性Jahn-Teller耦合强度g和非简谐耦合强度G的变化关系(a)Jx,y,(b)Jz,(c)

图5 自旋关联函数随Jahn-Teller线性耦合强度g和非简谐耦合强度G的变化
通过研究Jahn-Teller晶格-轨道耦合作用对基态性质的影响,发现Jahn-Teller效应并没有改变超交换作用下的自旋和轨道的结构,只是调整了Cu2+离子的轨道占据,从而改变了自旋和轨道间的关联强度.在超交换作用和Jahn-Teller效应的共同作用下(见表1),体系轨道在xy平面内反铁型排列,而沿z轴的两层间以反铁型方式排列(a型晶格结构)或铁型方式排列(d型晶格结构),并且轨道以-x2〉或方式占据,这使得自旋在双层间形成自旋单态,而在xy面间自旋单态间为弱的铁磁耦合,从而稳定了自旋二聚态基态.
3.1.3. 自旋二聚态的激发
在这一部分计算K3Cu2F7的基态自旋激发能隙.为了研究自旋激发,将轨道部分平均后得到自旋Hamilton量:

(5)式对应双层正方晶格结构的Heisenberg模型.对双层Heisenberg模型,当层间自旋耦合强度Jz与层内耦合强度Jx,y满足Jx,y/Jz∈(-0.4,0.3)时,体系的基态为自旋二聚态并可用键算符平均场方法来计算该体系的自旋激发[28—30].参照Matsushita处理双层Heisenberg模型得到的能谱色散关系[29],得到了自旋三重态激发能隙随Jahn-Teller晶格-轨道耦合强度g和G的变化曲线,如图6所示.由图6可知,当g=4.0 eV/和G=0.75g时自旋三态激发能隙≈326 K,比由磁化率推得的自旋能隙约400K略小[14].由于自旋-轨道具有强的耦合作用,自旋激发时必然伴随轨道的激发,即自旋激发实际是一种自旋-轨道的联合激发态.而轨道的空间分布的低对称性使得轨道激发为有能隙的激发,导致目前得到的自旋三重态激发能隙偏小.

图6 零温下,系统基态的自旋三重态激发能隙随Jahn-Teller线性耦合强度g和非简谐耦合强度G的变化
对Cs3Cu2Cl4Br3材料[13],其Cu2+离子处于CuCl4Br2八面体中心.因Cl-离子和Br-离子的半径大于F-离子半径,使得两Cu2+离子间Cu-X-Cu (X=F,Cl或Br)的间接跃迁强度比K3Cu2F7的大.跃迁强度的增强,导致Cs3Cu2Cl4Br3沿z轴的自旋耦合强度增大,从而表现为其自旋激发能隙约为2000K,比K3Cu2F7的能隙大得多.
4. 结论
利用团簇自洽场方法,研究了双层钙钛矿结构材料K3Cu2F7中形成自旋二聚态基态的微观机理,并计算了其自旋激发能隙.计算结果表明,在超交换作用和Jahn-Teller效应的共同作用下,体系轨道在xy平面内反铁型排列,而沿z轴的两层间以反铁型方式排列(a型晶格结构)或铁型方式排列(d型晶格结构),并且轨道以方式占据.这种轨道序使得自旋在双层间形成自旋单态,在xy面内自旋间为弱的铁磁耦合,并且自旋轨道的排列符合GKA规则,因此体系形成稳定的自旋二聚态基态.纯的超交换作用可以得到稳定的自旋二聚化基态,而Jahn-Teller效应起到了稳定和调节轨道占据的作用.由于没有考虑到自旋激发同时伴随的轨道激发,由键算符平均场方法得到的自旋能隙约为326 K,比实验值400K略小.该理论也适用于同类晶格结构的Cs3Cu2Cl4Br3的自旋二聚态的形成.
感谢中国科学院固体物理研究所邹良剑研究员的建议和讨论.
[1]Giamarchi T,Rueeggg C,Tchernyshyov O 2008 Nat.Phys.4 198
[2]Aczel A A,Kohama Y,Marcenat,Weickert F,Jaime M,Ayala-Valenzuela O E,McDonald R D,Luke G M 2009 Phys.Rev. Lett.103 207203
[3]Aczel A A,Jaime M,Ninios K,Chan H B,Balicas L,McDonald R D,Selesnic S D,Dabkowska H A,Luke G M 2009 Phys.Rev.B 79 100409(R)
[4]Tokura Y,Nagaosa N 2000 Science 288 462
[5]Shu L,Chen Y G,Chen H 2004 Acta Phys.Sin.53 902(in Chinese)[殳蕾、陈宇光、陈鸿2005物理学报53 902]
[6]Xu J,Wang Z G,Shi Y L,Chen Y G,Chen H 2004 Acta Phys. Sin.53 3882(in Chinese)[许靖、王志国、石云龙、陈宇光、陈鸿2004物理学报53 3882]
[7]Liu H L,Wang Z G,Chen Y G,Shi Y L,Chen H 2005 Acta Phys.Ain.54 2329(in Chinese)[刘海莲、王志国、陈宇光、石云龙、陈鸿2005物理学报54 2329]
[8]Liu H L,Wang Z G,Yang C Q,Shi Y L 2006 Acta Phys.Sin. 55 3688(in Chinese)[刘海莲、王志国、杨成全、石云龙2006物理学报55 3688]
[9]Ming X,Fan H G,Hu F,Wang C Z,Meng X,Huang Z F,Chen G 2008 Acta Phys.Sin.57 2368(in Chinese)[明星、范厚刚、胡方、王春忠、孟醒、黄祖飞、陈岗2008物理学报57 2368]
[10]Jackeli G,Ivanow D A 2007 Phys.Rev.B 76 132407
[11]Blundell S J,Lancaster T,Baker P J,Hayes W,Pratt F L,Atake T,Rana D S,Malik S K 2008 Phys.Rev.B 77 094424
[12]Chapon L C,Stock C,Radaelli P G,Martin C 2008 arXiv: 0807.0877
[13]Yamada F,Ono T,Tanaka H,Yamaura J 2007 J.Phys.Soc. Jpn.76 014708
[14]Manaka H,Miyashita Y,Watanabe Y,Masuda T 2007 J.Phys.Soc.Jpn.76 044710
[15]Quintero-Castro D L,Lake B,Wheeler E M,Islam A T M N,Guidi T,Rule K C,Izaola Z,Russina M,Kiefer K,Skourski Y 2010 Phys.Rev.B 81 014415
[16]Hirakawa K,Ikeda H 1973 J.Phys.Soc.Jpn.35 1328
[17]Castellani C,Natoli C R,Ranninger J 1978 Phys.Rev.B 18 4945
[18]Binggeli N,Altarelli M 2004 Phys.Rev.B 70 085517
[19]Liechtenstein A I,Anisimov V I,Zaanen J 1995 Phys.Rev.B 52 R5467
[20]Kanamori J 1960 J.Appl.Phys.31 14S
[21]Van Vleck J H 1939 J.Chem.Phys.7 72
[22]Zou L J,Liu H Q,Zheng Q Q 1998 J.Appl.Phys.83 7363
[23]Chen D M,Zou L J 2007 Int.J.Mod.Phys.B 21 691
[24]Liu D Y,Lu F,Zou L J 2009 J.Phys.:Condens.Matter 21 026014
[25]Liu D Y,Chen D M,Zou L J 2009 Chin.Phys.B 18 4497
[26]Herdtweck V E,Babel D 1981 Z.Anorg.Allg.Chem.474 113
[27]Goodenough J B 1958 Phys.Chem.Solids 6 287
[28]Sachdev S,Bhatt R 1990 Phys.Rev.B 41 9323
[29]Matsushita Y,Gelfand M P,Ishii C 1998 J.Phys.Soc.Jpn.68 247
[30]Yu D K,Gu Q,Wang H T,Shen J L 1999 Acta Phys.Sin.48 S169(in Chinese)[于登科、顾强、汪汉廷、沈觉涟1999物理学报48 S169]
PACC:7510J,7530E,7550E
*Project supported by the National Natural Science Foundation of China(Grant No.10947125)and the Scientific Research Starting Fund of China University of Petroleum(East China)of China(Grant No.Y081815).
†E-mail:dmchen@upc.edu.cn
Orbital ordering driven spin dimer state in double-layered antiferromagnet KCuO*327
Chen Dong-Meng1)†Liu Da-Yong2)
1)(College of Physical Science and Technology,China University of Petroleum,Dongying257061,China)
2)(Key Laboratory of Materials Physics,Institute of Solid State Physics,Chinese Academy of Sciences,Hefei230031,China)
(Received 9 March 2010;revised manuscript received 29 March 2010)
Magnetic,orbital and lattice structures of K3Cu2F7are determined by cluster self-consistent field approach based on the spin-orbital-lattice Hamiltonian.Symmetry breaking and Jahn-Teller distortion of approximately isolated bilayer cause Cu2+ions alternatively to occupyorbitals in each layer.This orbital ordering occupation leads to the dominant intrabilayer antiferromagnetic coupling,which favors spin dimerization,and the weak intralayer ferromagnetic coupling.Due to absence of spin frustration resulting from the intralayer orbital arrangement and the weak ferromagnetic coupling satisfing Goodenough-Kanamori-Anderson(GKA)rule,the ground state is a stable spin dimer state.The spin singlet-triplet excitation gap obtained by bond-operator mean field method is about 326 K,which is close to the experimental value of 400K.The present theory is also applicable to explaining the formation of spin dimer state in Cs3Cu2Cl4Br3.
spin dimer,orbital ordering,double-layered antiferromagnet K3Cu2F7
book=655,ebook=655
*国家自然科学基金(批准号:10947125)和中国石油大学(华东)科研启动基金(批准号:Y081815)资助的课题.
†E-mail:dmchen@upc.edu.cn

