闭合Λ型4能级系统中的电磁诱导透明和电磁诱导吸收*
李晓莉张连水 杨宝柱 杨丽君
(河北大学物理科学与技术学院,保定071002)
(2009年12月13日收到;2009年12月30日收到修改稿)
闭合Λ型4能级系统中的电磁诱导透明和电磁诱导吸收*
李晓莉†张连水 杨宝柱 杨丽君
(河北大学物理科学与技术学院,保定071002)
(2009年12月13日收到;2009年12月30日收到修改稿)
准Λ型4能级系统具有电磁诱导吸收(EIA)和电磁诱导透明(EIT)两种特性.准Λ型4能级系统包括两个基态精细结构能级和两个激发态精细结构能级,除光学耦合场和探测场外,附加了一个射频场作用于两个激发态精细结构能级之间.若对此系统进行拓展,在两个基态精细结构能级之间引入一个驱动场,则构成4场作用下的闭合Λ型4能级系统.本文对新引进的驱动场的作用规律进行了重点研究.研究结果表明,当驱动场和射频场的Rabi频率满足不同关系时,系统呈现EIA或EIT两种不同特性,探测吸收曲线的整体轮廓也随之改变.
电磁诱导透明,电磁诱导吸收,驱动场,射频场
PACC:4250
1. 引言
电磁诱导透明(EIT)和电磁诱导吸收(EIA)是光与物质相互作用中表现出来的一对性质相对立的相干现象,它们分别基于原子相干对吸收的相消干涉和相长干涉,使介质的吸收和色散特性发生完全不同的变化.目前,国内外对影响EIT和EIA线宽的诸多因素[1—4],以及外加驱动场对EIT或EIA的影响规律[5—10]都进行了大量的研究,但这些研究成果绝大多数是把EIT或EIA各自作为独立的现象进行研究得到的,而将EIT和EIA作为可相互转化的整体进行研究,并给出EIA和EIT的相互转化过程及物理本质的研究成果非常少[11—14].
在文献[13]中,我们对准Λ型4能级系统进行了分析和讨论.系统包括两个基态精细结构能级和两个激发态精细结构能级,除光学耦合场和探测场外,附加了一个射频场作用于两个激发态精细结构能级之间,并研究了通过改变光学耦合场的频率失谐量使系统的探测吸收谱呈现EIA和EIT两种完全相反的特性.由于基态精细结构能级之间的相干失相速率很小,因此EIT和EIA具有极窄的光谱线宽,比光学跃迁的自然线宽小几个数量级.本文对上述准Λ型4能级系统进行拓展,在两个基态精细结构能级之间引入另一个射频场(为了与原来的射频场区分开,称其为驱动场),则构成了4场作用下的闭合Λ型4能级系统.本文对新引进的驱动场对系统的影响规律进行了重点研究,发现当驱动场和射频场的Rabi频率满足不同关系时,系统呈现EIA或EIT两种不同特性,而且探测吸收曲线的整体轮廓也随之改变,同时给出了相应的缀饰态解释[15].
2. 系统的密度矩阵方程
光学耦合场、射频场、驱动场和探测场共同作用下的闭合Λ型4能级系统模型如图1(a)所示.其中,〉和能级属基态精细结构能级,〉和能级属激发态精细结构能级.频率为ωc的光学耦合场激励跃迁,频率为ωrf的射频场激励跃迁,新引进频率为ωd的驱动场激励跃迁,而频率为ωp的探测场通过扫描跃迁获得探测吸收谱.4个场的Rabi频率分别为Ωc,Ωrf,Ωd和Ωp.

图1 光学耦合场、射频场、驱动场和探测场共同作用下的闭合Λ型4能级系统(a)裸态能级图;(b)当驱动场不存在,只有射频场(Ωrf=2)作用时的缀饰态能级图;(c)驱动场和射频场的Rabi频率相等(Ωd=Ωrf=2)时的缀饰态能级图;(d)驱动场的Rabi频率小于射频场的Rabi频率(Ωd=1,Ωrf=2)时的缀饰态能级图;(e)驱动场的Rabi频率大于射频场的Rabi频率(Ωd=3,Ωrf=2)时的缀饰态能级图
闭合Λ型4能级系统的密度矩阵方程可表示为
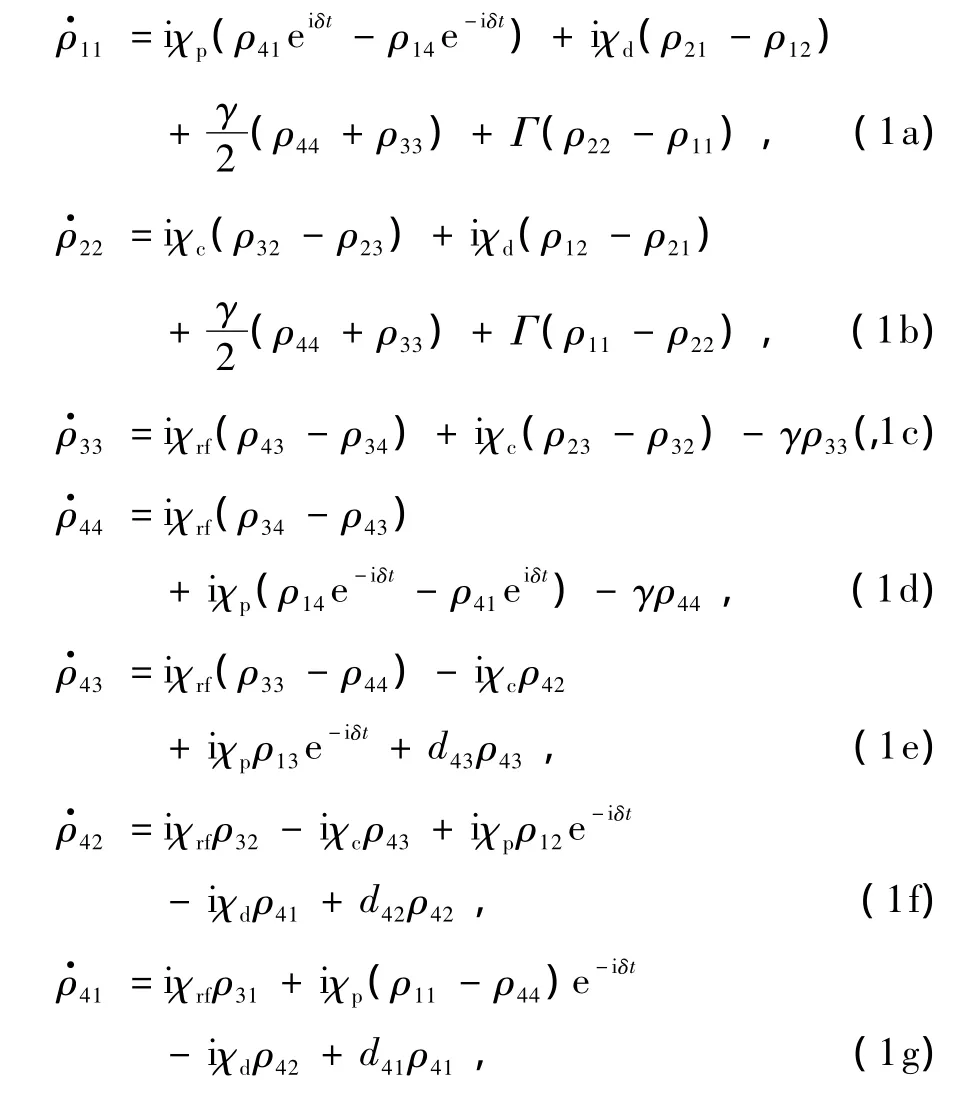
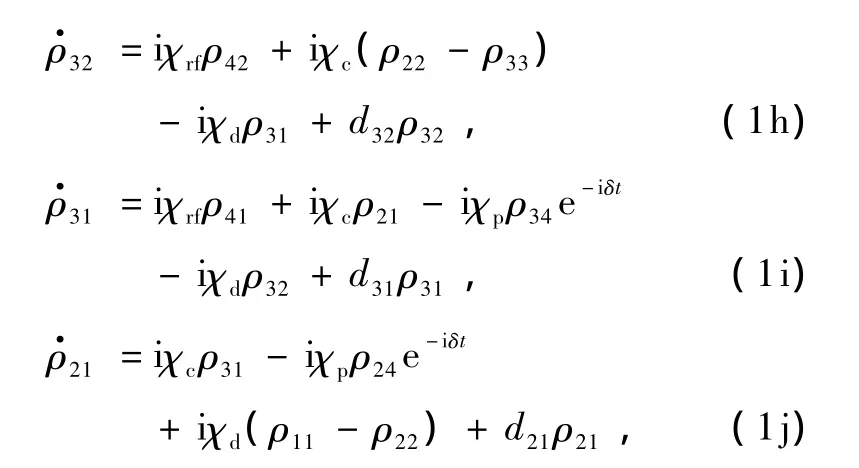
这里,χc=Ωc/2,χrf=Ωrf/2,χd=Ωd/2,χp=Ωp/2. dij=iδij-γij为复失谐量,其中,δij分别为δ32=ωcω32,δ43=ωrf-ω43,δ21=ωd-ω21,δ41=ωp-ω41, γij是能级和之间的相干失相速率.激发态能级和自发衰减到基态能级和的粒子数衰减速率均为γ,而和之间的粒子数弛豫速率均为Γ.为简单起见,设γ=1,其他参量均以其为单位取相对值.
密度矩阵方程中的非对角密度矩阵元ρ41的虚部正比于探测场的吸收系数,实部则反映探测场的色散特性.本工作重在研究驱动场和射频场对系统的影响,故将探测场视为弱场.通过对探测场进行微扰处理,求解ρ41的一级微扰解,得到lm[ρ(1)41]随探测场失谐量δ41=ωp-ω41的变化曲线,即探测吸收谱的变化规律.ρ41的一级微扰解表达式为
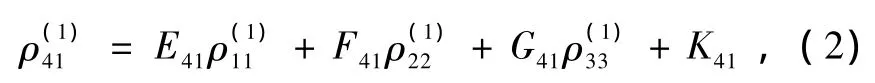
其中,ρ(1)11,ρ(1)22和ρ(1)33为一阶粒子数,K41是与零级解ρ(0)11,ρ(0)44,ρ(0)24,ρ(0)34,ρ(0)12和ρ(0)13有关的参量.
3. 结果和讨论
3.1. 探测吸收曲线随驱动场Rabi频率的变化
文献[13]中已经对光学耦合场的作用规律进行了分析和讨论,本文将重点考虑驱动场和射频场对系统的影响规律.因篇幅限制,本文只讨论光学耦合场、射频场和驱动场均共振作用时探测吸收曲线的变化规律.
首先讨论驱动场对系统的影响规律.图2给出了闭合Λ型4能级系统中,其他参数保持不变,探测吸收曲线随驱动场Rabi频率增大时的变化规律. 4条曲线均对应于光学耦合场与跃迁、射频场与跃迁以及驱动场与跃迁共振的情况,其中Ωc=0.1,Ωrf=2.图2(a)为没有附加驱动场的情况(Ωd=0),此时探测吸收曲线的中心频率处出现的不是EIT,而是线宽极窄的EIA.同时由于射频场的动态Stark劈裂效应,在探测场的频率失谐量为δp=±1处分别出现了一个线宽接近于自然线宽的强吸收峰,被称为Autler-Townes双峰.这时的探测吸收曲线与文献[13]中讨论的准Λ型4能级系统的探测吸收曲线完全吻合.图2(b)为驱动场的Rabi频率Ωd=1的情况,此时的探测吸收曲线在探测场的频率失谐量为δp=±1处出现了线宽极窄、吸收特性介于EIT和EIA之间的一种非线性现象.同时由于射频场和驱动场共同作用引起的动态Stark劈裂效应,探测吸收曲线上出现了4个强吸收峰,它们分别出现在探测场的频率失谐量为δp=±0.5和δp=±1.5处.图2(c)为驱动场的Rabi频率Ωd=2的情况,此时的探测吸收曲线在探测场的频率失谐量为δp=±2处出现了线宽极窄的EIT.同时出现了3个强吸收峰,其中一个位于中心频率处,另外两个分别出现在探测场的频率失谐量为δp=±2处,与EIT叠加在一起.图2 (d)为驱动场的Rabi频率Ωd=3的情况,此时的探测吸收曲线在探测场的频率失谐量为δp=±3处出现了EIT,并分别在δp=±0.5和δp=±2.5处出现了4个强吸收峰.此时的EIT与4个强吸收峰之间没有任何交叠,EIT移动到了4个强吸收峰的外侧.
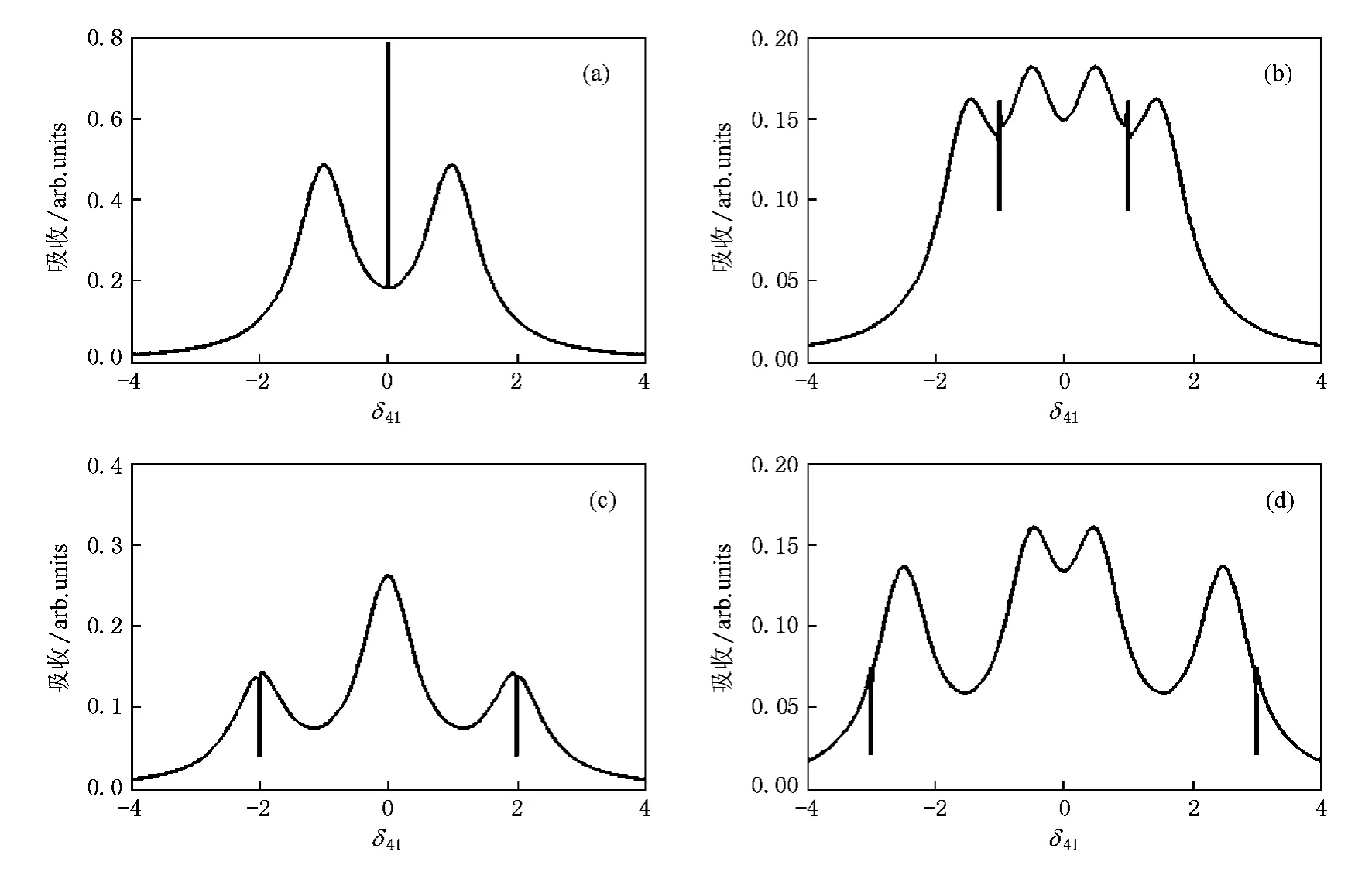
图2 闭合Λ型4能级系统在射频场(Ωrf=2)和驱动场共振,且驱动场的Rabi频率分别取0,1,2和3时的探测吸收曲线
通过图2的4条曲线得出如下结论,探测吸收曲线在与驱动场的Rabi频率相对应的探测频率处出现了线宽极窄的EIA或EIT,而且随着驱动场的Rabi频率取值不同,系统呈现不同的非线性特性.在图2(a)中,Ωd=0,探测吸收曲线上出现了EIA;在图2(b)中,Ωd=1,出现的是吸收特性介于EIT和EIA之间的一种非线性现象;而在图2(c)和(d)中,分别为Ωd=2和Ωd=3,出现的是EIT.这表明,保持其他参数不变时,随着驱动场Rabi频率的增加,系统中出现了从EIA向EIT的过渡.因此,在闭合Λ型4能级系统中,驱动场的作用非常重要,它会使系统的非线性特性发生本质的改变,使系统呈现EIT或EIA这样一对性质相对立的相干现象,并能通过改变驱动场的Rabi频率控制EIT或EIA的频率位置.
3.2. 探测吸收曲线随射频场Rabi频率的变化
场的Rabi频率时得到的.为了更全面地了解闭合Λ型4能级系统中EIA和EIT的转化规律,下面讨论射频场对系统的影响规律.
图3给出了闭合Λ型4能级系统中,其他参数保持不变,探测吸收曲线随射频场Rabi频率增大时的变化规律.4条曲线均对应于光学耦合场与跃迁、射频场与跃迁和驱动场与跃迁共振的情况,其中Ωc=0.1,Ωd=2. 4条曲线中,除了图3(a)既没有出现EIT,也没有出现EIA之外,其他的3条曲线均在探测场的频率失谐量为δp=±2处出现了EIT或EIA现象.这一现象再次证明了在闭合Λ型4能级系统中,驱动场对于EIT或EIA的形成具有主导性作用,EIA或EIT总是出现在与驱动场的Rabi频率相对应的探测频率处.
上述结论是在保持其他参数不变,只改变驱动

图3 闭合Λ型4能级系统在驱动场(Ωd=2)和射频场共振,且射频场的Rabi频率分别取0,1,2和3时的探测吸收曲线
下面讨论射频场在EIA或EIT的形成过程中所起的作用,以及对整个系统的影响规律.图3(a)为没有附加射频场的情况(Ωrf=0),此时探测吸收曲线上既没有出现EIT,也没有出现EIA.仅仅由于驱动场的动态Stark劈裂效应,在探测场的频率失谐量为δp=±1处出现了Autler-Townes双峰.图3(b)为射频场的Rabi频率Ωrf=1的情况,此时在探测吸收曲线上出现的是EIT,并分别在探测场的频率失谐量为δp=±0.5和δp=±1.5处出现了4个强吸收峰.此时EIT已经位于4个强吸收峰的外侧,它们之间没有任何交叠.图3(c)为射频场的Rabi频率Ωrf=2的情况,此时在探测吸收曲线上出现的依然是EIT,并分别在探测场的频率失谐量为δp=0和δp=±2处出现了3个强吸收峰,其中两个边峰与EIT叠加在一起,这条曲线与图2(c)具有完全相同的参数,得到的结果也完全相同.图3(d)为射频场的Rabi频率Ωrf=3的情况,此时在探测吸收曲线上出现的是吸收特性介于EIT和EIA之间的一种非线性现象,并分别在δp=±0.5和δp=±2.5处出现了4个强吸收峰.
通过图3的4条曲线得出如下结论,保持其他参数不变时,随着射频场Rabi频率的增加,系统中出现了从EIT向EIA的过渡.因此,在闭合Λ型4能级系统中,射频场对于EIT或EIA的形成具有重要的辅助作用,它和驱动场的共同作用使系统呈现出EIT或EIA这样一对性质相对立的相干现象.
另外,驱动场与射频场的共同作用影响着系统探测吸收曲线的轮廓.由于驱动场和射频场都可以使原子能级发生动态Stark劈裂效应,因此它们的Rabi频率大小决定了线宽接近于自然线宽的强吸收峰的个数、强度以及频率位置.例如,在图2(a)和图3(a)中,在射频场(Ωrf=2)或驱动场(Ωd=2)单独存在的情况下,探测吸收曲线上均出现了位于探测场的频率失谐量为δp=±1处的两个强吸收峰.在图2(c)和图3(c)中,同时引入驱动场和射频场,而且它们的Rabi频率相等,Ωrf=Ωd=2,探测吸收曲线上出现了3个强吸收峰,其中一个位于中心频率处,另外两个位于探测场的频率失谐量为δp=±2处.在图2(b)和图3(b)中,驱动场和射频场的Rabi频率不同,分别为Ωrf=2,Ωd=1和Ωrf=1,Ωd=2,但两种情况下驱动场和射频场的Rabi频率正好相反,因此两图中的探测吸收曲线上均出现了位于探测场的频率失谐量为δp=±0.5和δp=± 1.5处的4个强吸收峰.同理,在图2(d)和图3(d)中,驱动场和射频场的Rabi频率分别为Ωrf=2,Ωd=3和Ωrf=3,Ωd=2,探测吸收曲线上均出现了位于探测场的频率失谐量δp=±0.5和δp=±2.5处的4个强吸收峰.结果表明,由驱动场和射频场的动态Stark劈裂效应产生的强吸收峰总是出现在探测场的频率失谐量和处,这一点很容易通过后面的缀饰态理论得到解释.
3.3. 缀饰态解释
前面的分析表明闭合Λ型4能级系统中EIA向EIT的转化经过了一系列的中间变化过程,而且驱动场和射频场在其中各自起到了不同的作用.此系统中探测吸收特性的形成机理可用缀饰态理论得到很好的解释[15].在本研究中,相对于能级之间的跃迁线宽而言,射频场可视为强场,由其产生的动态Stark 劈裂效应使能级劈裂为两条缀饰态能级和.同理,作用于能级之间的驱动场也产生动态Stark劈裂效应,使能级劈裂为两条缀饰态能级和.由于射频场和驱动场均与对应能级发生共振相互作用,因此和对称地分布在原子能级的两侧,其能级间距等于射频场的Rabi频率Ωrf,而且和对称地分布在原子能级的两侧,其能级间距等于驱动场的拉比频率Ωd.本文采用的探测场通过扫描跃迁获得探测吸收谱,故缀饰态能级和与缀饰态能级和之间的跃迁,使探测吸收曲线上出现了位于探测场的频率失谐量δp=和处的线宽接近于自然线宽的强吸收峰.
下面重点解释EIA和EIT的形成及转化过程.在文献[13]中已经讨论了EIA的产生机理,如图1 (b)所示.当驱动场不存在(Ωd=0)时,只有射频场(Ωrf=2)产生的动态Stark 劈裂效应使能级劈裂为两条缀饰态能级和.由于光学耦合场与能级共振,射频场与能级共振,原子在这两个激光场的作用下形成了从能级到虚能级再到能级的跃迁路径,即原子从能级到能级再到能级上和从能级到能级再到能级上,形成了两条量子通道.由于这两条量子通道具有大小相同的调谐频率而符号相反,它们之间形成量子相干,使介质的吸收特性发生改变,在探测场的中心频率处感应形成EIA.
再来看本系统中双EIT的形成过程,如图1(c)所示.当驱动场和射频场的Rabi频率相等(Ωd= Ωrf=2)时,射频场产生的动态Stark劈裂效应使能级劈裂为两条缀饰态能级和,驱动场产生的动态Stark 劈裂效应使能级劈裂为两条缀饰态能级和同时使能级劈裂为两条缀饰态能级和和和〉以及和能级间距均等于2.由于光学耦合场与能级共振,射频场与能级共振,原子在这两个激光场的作用下形成了两条跃迁路径,一条是从能级到能级再到能级,另一条是从能级到能级再到能级,这两条跃迁路径互不相干,分别构成Λ型3能级系统,在探测场的频率失谐量为δ41=±2处形成EIT.
对于从EIA向EIT转化的中间过程可以用图1 (d)来解释.当驱动场的Rabi频率小于射频场的Rabi频率(Ωd=1,Ωrf=2)时,缀饰态能级和之间的能级间距等于2,缀饰态能级和及和之间的能级间距均等于1.当光学耦合场与能级共振,射频场与能级共振时,原子具有两条跃迁路径,一条是从能级到上虚能级再到能级,另一条是从能级到下虚能级再到能级.上下两条虚能级之间的能级间距等于1,比和之间的能级间距小,所以原子从能级到上虚能级再到能级的跃迁路径是从能级到能级再到能级和从能级到能级再到能级的量子通道相干作用的结果.但由于此跃迁路径距离第一条量子通道较近,而距离第二条量子通道较远,所以此跃迁路径除了表现出两条量子通道的相干结果外,由于受到第一条量子通道的影响较大,在探测场的频率失谐量为δ41=1处呈现出一种介于EIA和EIT之间的非线性现象.同理,原子从能级到下虚能级再到能级的跃迁路径使介质在探测场的频率失谐量为δ41=-1处呈现出一种介于EIA和EIT之间的非线性现象.
图1(e)说明了当驱动场的Rabi频率大于射频场的Rabi频率(Ωd=3,Ωrf=2)时,系统只呈现EIT特性.缀饰态能级和之间的能级间距等于2,缀饰态能级和以及和之间的能级间距均等于3.当光学耦合场与、射频场与能级共振时,原子具有两条跃迁路径,一条是从能级到上虚能级再到能级,另一条是从能级到下虚能级再到能级.上下两条虚能级之间的能级间距等于3,比和之间的能级间距大.虽然原子从能级到上虚能级再到能级的跃迁路径仍然是从能级到能级再到能级的量子通道和从能级到能级4-〉再到能级的量子通道相干作用的结果,但由于此跃迁路径距离第一条量子通道较近,而距离第二条量子通道非常远,所以此跃迁路径受到第二条量子通道的影响几乎可以忽略,主要受到第一条量子通道的影响,在探测场的频率失谐量为δ41=3处呈现出EIT的特性.同理,原子从能级到下虚能级再到能级的跃迁路径使介质在探测场的频率失谐量为δ41=-3处呈现出EIT的特性.
综上所述,在闭合Λ型4能级系统中,当驱动场不存在时,在探测场的中心频率δ41=0处感应形成EIA;当驱动场和射频场的Rabi频率相等或驱动场的Rabi频率大于射频场的Rabi频率时,在探测场的频率失谐量为δ41=±Ωd处形成EIT;当驱动场的Rabi频率小于射频场的Rabi频率时,在探测场的频率失谐量为δ41=±Ωd处呈现出一种介于EIA和EIT之间的非线性现象.
4. 结论
对4场作用下的闭合Λ型4能级系统的探测吸收特性进行了理论研究,分析了EIA和EIT的产生条件以及相互转化过程,并利用缀饰态理论给出了合理解释.研究表明,在本系统中,当光学耦合场、驱动场和射频场均为共振作用时,可以通过改变驱动场和射频场的Rabi频率使系统的非线性特性发生本质的改变,使系统呈现EIT或EIA这样一对性质相对立的相干现象,并能通过改变驱动场的Rabi频率控制EIT或EIA的频率位置.该研究结果对EIA和EIT在量子计算[16,17]和光信息存储[18—21]等领域的应用研究具有重要意义.
[1]Javan A,Kocharovskaya O,Lee H,Scully M O 2002 Phys. Rev.A 66 013805
[2]Ye C Y,Zibrov A S 2002 Phys.Rev.A 65 023806
[3]Yang L J,Zhang L S,Li X L,Feng X M,Fu G S,Han L 2004 Proc.SPIE 5631 196
[4]Dimitrijevic J,Arsenovic D,Jelenkovic B M 2007 Phys.Rev.A 76 013836
[5]Wilson E A,Manson N B,Wei C J 2005 Phys.Rev.A 72063814
[6]Wilson E A,Manson N B,Wei C J,Yang L J 2005 Phys.Rev. A 72 063813
[7]Yang L J,Zhang L S,Li X L,Han L,Fu G S,Manson N B,Suter D,Wei C J 2005 Phys.Rev.A 72 053801
[8]Yang L J,Zhang L S,Li X L,Li X W,Guo Q L,Han L,Fu G S 2006 Acta Phys.Sin.55 5206(in Chinese)[杨丽君、张连水、李晓莉、李晓苇、郭庆林、韩理、傅广生2006物理学报55 5206]
[9]Li H,Sautenkov V A,Rostovtsev Y V,Welch G R,Hemmer P R,Scully M O 2009 Phys.Rev.A 80 023820
[10]Zhukov A A,Zibrov S A,Romanov G V,Dudin Y O,Vassiliev V V,Velichansky V L,Yakovlev V P 2009 Phys.Rev.A 80 033830
[11]Zhang J P,Xu J,Hernandez G,Hu X M,Zhu Y F 2007 Phys. Rev.A 75 043810
[12]Fu G S,Li X L,Zhuang Z H,Zhang L S,Yang L J,Li X W,Han L,Manson N B,Wei C J 2008 Phys.Lett.A 372 176
[13]Zhang L S,Li X L,Wang J,Yang L J,Feng X M,Li X W,Fu G S 2008 Acta Phys.Sin.57 4921(in Chinese)[张连水、李晓莉、王健、杨丽君、冯晓敏、李晓苇、傅广生2008物理学报57 4921]
[14]Yang X H,Zhu S Y 2008 Phys.Rev.A 78 023818
[15]Cohen-Tannoudji C,Dupont-Roc J,Grynberg G 1992 Atom-Photon Interactions:Basic Processes andApplications(New York:Wiley)
[16]Yang X,Tong Z Y,Kuang L M 2008 Acta Phys.Sin.57 1689 (in Chinese)[杨雄、童朝阳、匡乐满2008物理学报57 1689]
[17]Cheng Q L,Xie S Y,Yang Y P 2008 Acta Phys.Sin.57 6968 (in Chinese)[成秋丽、谢双媛、羊亚平2008物理学报57 6968]
[18]Ghosh J,Ghosh R,Goldfarb F,Gouet J L,Bretenaker F 2009 Phys.Rev.A 80 023817
[19]Yannopapas V,Paspalakis E,Vitanov N V 2009 Phys.Rev.B 80 035104
[20]Schnorrberger U,ThompsonJ D,TrotzkyS,PugatchR,Davidson N,Kuhr S,Bloch I 2009 Phys.Rev.Lett.103 033003
[21]Lu H,Tian H P,Li C H,Ji Y F 2009 Acta Phys.Sin.58 2049 (in Chinese)[鲁辉、田慧平、李长红、纪越峰2009物理学报58 2049]
PACC:4250
*Project supported by the Natural Science Foundation of Hebei Province,China(Grant No.A2009000140)and the Natural Science Foundation of Hebei University,China(Grant No.2008Q14).
†E-mail:xiaolixiaoli001@yahoo.com.cn
Electromagnetically induced absorption and transparency in a closed lambda-shaped four-level system*
Li Xiao-Li†Zhang Lian-Shui Yang Bao-Zhu Yang Li-Jun
(College of Physical Science and Technology,Hebei University,Baoding071002,China)
(Received 13 December 2009;revised manuscript received 30 December 2009)
A quasi-lambda four-level system shows both electromagnetically induced absorption(EIA)and electromagnetically induced transparency(EIT).In addition to an optical coupling field and a probing field,there is a radio field which interacts with two excited state hyperfine levels of the quasi-lambda four-level system consisting of two excited state hyperfine levels and two ground state hyperfine levels.If a driving field which interacts with two ground state hyperfine levels is introduced,the quasi-lambda four-level system is modified to a closed-lambda four-level system.The behaviors of the driving field and radio field are studied in this paper and it is seen that the occurence of EIA or EIT and the whole probing properties are controlled by the Rabi frequencies of both driving field and radio field.
electromagnetically induced transparency,electromagnetically induced absorption,driving field,radio field
book=708,ebook=708
*河北省自然科学基金(批准号:A2009000140)和河北大学自然科学研究计划(批准号:2008Q14)资助的课题.
†E-mail:xiaolixiaoli001@yahoo.com.cn

