基于反转法的O2-CO2输运性质预测*

王晓坡 宋渤 吴江涛刘志刚

(西安交通大学动力工程多相流国家重点实验室，西安710049)

(2009年11月19日收到;2010年1月14日收到修改稿)

基于反转法的O2-CO2输运性质预测*

王晓坡 宋渤 吴江涛†刘志刚

(西安交通大学动力工程多相流国家重点实验室，西安710049)

(2009年11月19日收到;2010年1月14日收到修改稿)

采用反转法计算得到了O2-CO2混合气体新的势能参数.在此基础上，根据分子动力学理论，计算了混合气体在零密度下的输运性质，包括黏度系数、热扩散系数和热扩散因子，计算的温度范围为273.15—3273.15 K.与实验值比较表明，计算结果可以满足实际工程应用.

O2-CO2混合物，输运性质，反转法，新势能

PACC:5110，5225F，3180，3420

1. 引言

分子间的相互作用力决定了物质的性质.在计算气体输运性质过程中，确定势能模型至关重要［1—4］.势能模型可以通过实验回归或者理论计算得到.通过实验数据(比如Virial系数、气相黏度、音速等)回归时，由于目前常用的势能模型一般都仅有几个可调参数，因此精度不高，同时，通过不同性质回归得到的势能参数往往也不相同.鉴于此，Smith等［5］提出了反转法来计算势能参数，该方法不依赖于特定的势能模型，只需假定一初始参数，通过迭代即可得到气体的新势能.近年来，Najafi等和Papari等［6，7］对这种方法进行了研究改进，提高了其计算精度.

O2/CO2混合气体循环燃烧技术可以大幅度减少SO2和NOx排放，实现污染物的一体化协同脱除，被认为是回收隔离CO2的一个重要手段［8］.因此对于O2-CO2混合气的相关热物理性质研究具有十分重要的现实意义和工业价值.

鉴于O2-CO2混合气输运性质在实际应用中的重要性且文献中还未见对其进行过深入的理论研究，本文采用反转法计算得到了O2-CO2混合气体的新势能，并在此基础上根据分子动力学理论，计算了混合气体在零密度下的输运性质，包括黏度系数η，热扩散系数D和热扩散因子αT，计算的温度范围为273.15—3273.15 K.

2. 理论计算模型

2.1. 反转法原理

根据分子动力学理论［9］，气体在零密度时的碰撞积分Ω(l，s)(T)定义为

其中，T为温度，l和s为输运参数，E为碰撞的相对能量，Q(l)(E)为碰撞截面，其定义为

(2)式中b为碰撞参数，θ为碰撞偏斜角，且有

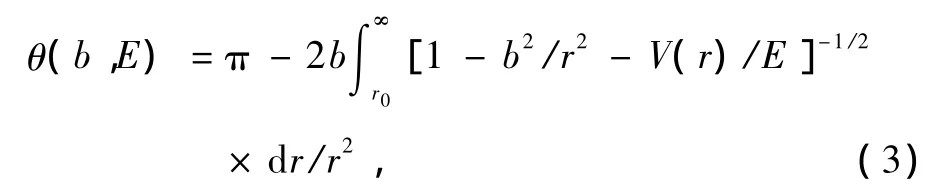
其中V(r)为势能，r为分子间距离，而r0为碰撞时分子间的最短距离，可由下式计算得到:

在采用反转法时，如果任意假定一个势模型(例如Lennard-Jones(12-6)势能模型)，且给定一组对比黏度碰撞积分Ω*(2，2)(T)［10］，那么就可以通过下式计算得到势能V(r)和分子间距离r:

这里σ和ε分别为势阱位置和势阱深，G为仅与温度有关的反转函数.(1)—(6)式经过迭代后，可以计算得到新的势能V(r).

2.2. 混合物的输运系数

如果已知碰撞积分，O2-CO2混合物的输运系数，包括黏度系数η，热扩散系数D，热扩散因子αT可由下列公式计算得到.

2.2.1. 黏度系数η

2.2.2. 热扩散系数D

2.2.3. 热扩散因子αT

(7)—(19)式中，x表示组分的摩尔分数，m表示组分的摩尔质量，kB为Boltzmann常数，P为大气压强(其值为101325 Pa)，Δij为扩散系数的修正项，kT为热扩散因子的修正项，一般可忽略不计.下脚标i和j分别表示混合物中重组分和轻组分.特征参数A*，B*，C*，E*和F*可由下式计算得到:

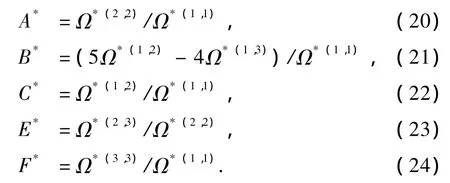
3. 结果与讨论

目前，已有许多研究人员对纯质CO2在零密度时的黏度系数和热扩散系数进行了深入研究［11—15］，得到了比较可靠的结果.因此为了验证本文工作的正确性，我们以LJ(12-6)势能模型作为初始给定的势能模型，利用反转法首先计算了CO2零密度下300—3500K温度范围内的黏度系数η，热扩散系数D和热扩散因子αT，计算结果列于表1.同时图1和2还给出了本文黏度系数和热扩散系数计算结果与文献的相对偏差(Dev)分布.从图中可以看出，除个别点外，本文计算得到的CO2黏度系数和热扩散系数与文献值的偏差分别在2.0%和4.0%以内，说明结果具有较高的计算精度，可以进行其他相关物质迁移性质的理论计算.

表1 CO2的黏度系数η，热扩散系数D和热扩散因子αT

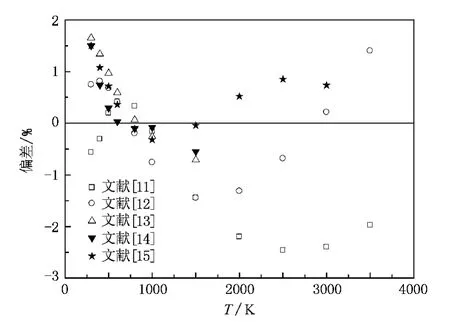
图1 CO2黏度系数计算结果与文献值的偏差

图2 CO2热扩散系数计算结果与文献值的偏差

在此基础上，本文经过迭代计算得到了O2-CO2的新势能函数.根据得到的新势能，计算了一定温度范围内O2-CO2的特征参数A*—F*，如表2所示.同时根据分子动力学理论，分别计算了等摩尔O2-CO2零密度时的黏度系数η，热扩散系数D和热扩散因子αT，计算的温度范围为273.15—3273.15 K，计算结果列于表3.

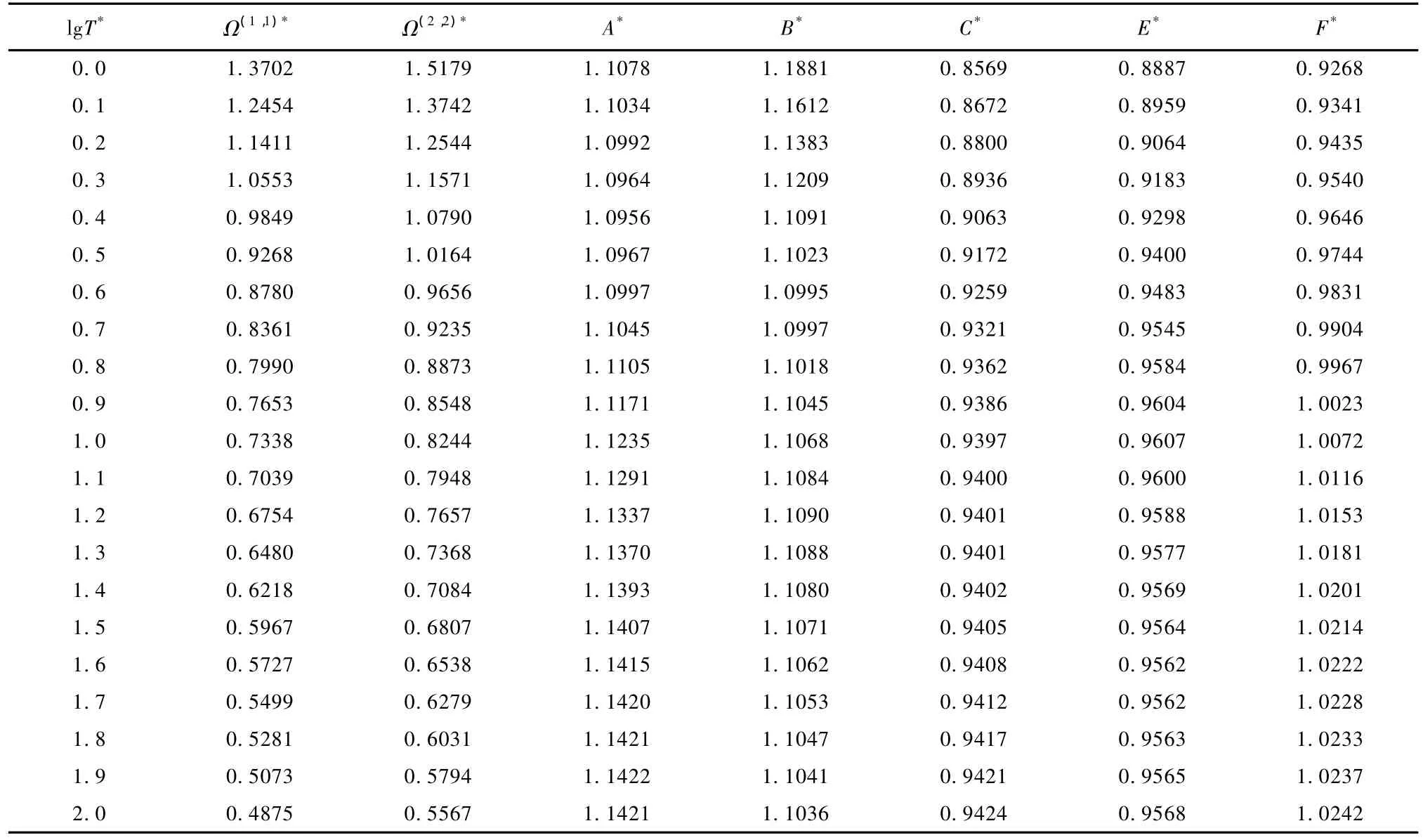
表2 O2-CO2的碰撞积分和特征参数

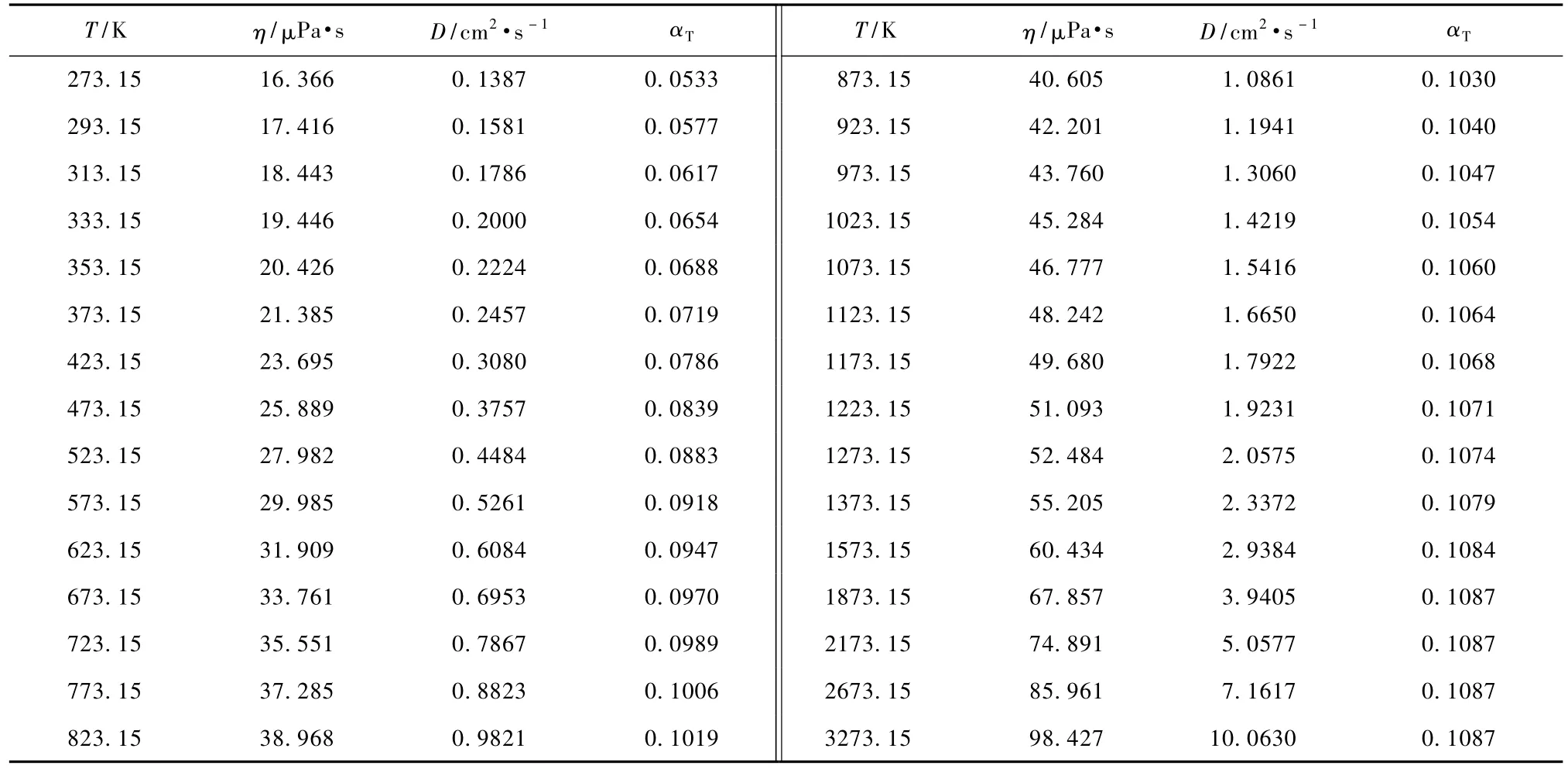
表3 等摩尔O2-CO2的黏度系数η，热扩散系数D和热扩散因子αT

图3给出了本文计算得到的等摩尔时O2-CO2黏度系数和扩散系数与文献［15］计算值的相对偏差分布，黏度计算值与文献［15］的绝对平均偏差和最大偏差分别为0.68%和1.22%，扩散系数计算值与文献［15］的绝对平均偏差和最大偏差分别为2.98%和5.19%.

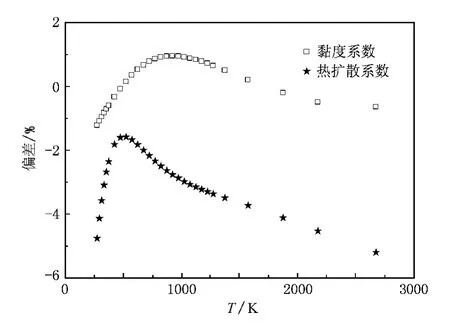
图3 等摩尔时黏度系数和热扩散系数计算结果与文献［15］的偏差

图4给出了O2-CO2混合物在温度范围为300—700K间不同O2摩尔比例(xO2)时，本文计算得到的黏度值与实验值［16］的偏差分布，其绝对平均偏差和最大偏差分别为2.11%和3.92%.图5给出了本文计算得到的扩散系数值和实验值［16—18］的偏差分布，从图中可以看出，最大偏差在4.0%以内.结果表明本文计算结果可以满足实际工程需要.由于热扩散因子在文献中未见报道，因此本文在这里没有进行比较.

图4 不同摩尔比例下黏度系数的计算值与实验值［16］的偏差

图5 热扩散系数计算值与实验值的偏差

4. 结论

本文利用反转法，计算得到了O2-CO2混合气体的新势能参数.在此基础上，分别计算得到了O2-CO2零密度时的黏度系数η，热扩散系数D和热扩散因子αT，计算的温度范围为273.15—3273.15 K.通过与文献数据比较，说明本文计算得到的结果具有较高的精度，可以满足实际工程应用.

［1］Guo J J 2002 Acta Phys.Sin.51 497(in Chinese)［郭建军2002物理学报51 497］

［2］Shao J X，Zhu Z H，Huang D H，Wang J，Cheng X L，Yang X D 2007 Chin.Phys.16 2650

［3］Yu C R，Wang R K，Cheng X L，Yang X D 2007 Acta Phys. Sin.56 2577(in Chinese)［余春日、汪荣凯、程新路、杨向东2007物理学报56 2577］

［4］Yu C R，Song X S，Cheng X L，Yang X D，Shen C S 2008 Acta Phys.Sin.57 3446(in Chinese)［余春日、宋晓书、程新路、杨向东、申传胜2008物理学报57 3446］

［5］Gough D W，Maitland G C，Smith E B 1972 Mol.Phys.24 151

［6］Goharshadi E K，JamiAlahmadi M，Najafi B 2003 Can.J. Chem.81 866

［7］Haghighi B，Fathabadi M，Papari M M 2002 Fluid Phase Equilibr.203 205

［8］Liu Z，Song Q，Yao Q，Zhang L Q 2007 J.North China Electric Power Univ.34 82(in Chinese)［刘忠、宋蔷、姚强、张利琴2007华北电力大学学报34 82］

［9］Hirschfelder J O，Curtiss C F，Bird R B 1954 Molecular Theory of Gases and Liquids(New York:John Wiley)

［10］Bzowski J，Kestin J，Mason E A，Uribe F J 1990 J.Phys. Chem.Ref.Data 19 1179

［11］Abbaspour M，Goharshadi E K 2006 Chem.Phys.330 313

［12］Papari M M 2003 Chem.Phys.288 249

［13］Bock S，Bich E，Vogel E，Dickinson A S，Vesovic V 2002 J. Chem.Phys.117 2151

［14］Trengove R D，Wakeham W A 1987 J.Phys.Chem.Ref.Data 16 175

［15］Lemmon E W，McLinden M O，Huber M L 2003 NIST Reference Fluid Thermodynamic and Transport Properties Version 7.1. (Gaithersburg:National Institute of Standards and Technology)

［16］Kestin J，Khalifa H E，Ro S T，Wakeham W A 1977 Physica 88A 242

［17］Waldmann L 1947 Z.Phys.A Hadron.Nucl.124 2

［18］Walker R E，Westenberg A A 1960 J.Chem.Phys.32 436

PACC:5110，5225F，3180，3420

*Project supported by the National Natural Science Foundation of China(Grant No.50836004)and the Foundation for the Author of National Excellent Doctoral Dissertation of China(Grant No.200540).

†Corresponding author.E-mail:jtwu@mail.xjtu.edu.cn

Prediction of transport properties of O2-CO2mixtures based on the inversion method*

Wang Xiao-Po Song Bo Wu Jiang-Tao†Liu Zhi-Gang
(State Key Laboratory of Multiphase Flow in Power Engineering，Xi'an Jiaotong University，Xi'an710049，China)
(Received 19 November 2009;revised manuscript received 14 January 2010)

A new potential energy surface of O2-CO2mixtures was obtained by means of inversion method.According to the kinetic theory of gas，the transport properties of O2-CO2mixtures，including viscosity coefficient，thermal diffusion coefficient and thermal diffusion factor，were caluclated in the temperature range between 273.15 K and 3273.15 K at zero-density.

O2-CO2mixtures，transport properties，inversion method，potential energy surface

book=688,ebook=688

*国家自然科学基金重点项目(批准号:50836004)和全国优秀博士学位论文作者专项资金(批准号:200540)资助的课题.

†通讯联系人.E-mail:jtwu@mail.xjtu.edu.cn