关于耳板式吊耳设计校核的探讨

■万进 杨刚军 湖北金石炼化建设有限公司湖北荆门448000

关于耳板式吊耳设计校核的探讨

■万进 杨刚军 湖北金石炼化建设有限公司湖北荆门448000

通过分析耳板式吊耳的受力情况和设计原理，结合实际情况指出在实际工程应用中的不足和失误，以求保障设备吊装过程尤其是大型设备吊装能顺利安全进行。

耳板式吊耳受力分析强度校核

在设备安装工程的建设过程中，设备吊装始终处在举足轻重的位置。设备吊装过程尤其是大型设备吊装是否能顺利安全进行，直接决定着工程项目的施工周期和项目投资，更关系到工程项目管理的成败、企业市场开发与经营运行效果和企业的持续发展。

吊耳是设备吊装过程中最直接的受力部件，常用的形式分为耳板式和管轴式，分别应用在中小型和大中型的设备吊装工程中，且耳板式较管轴式应用范围更广一些，应用时常常是根据相关规范选用。但在实际工作中，对于管轴式吊耳，所有工程技术人员基本上都是严格按照规范选用和制造；而对于耳板式吊耳，规范的执行并不是很严格，并且由于耳板式吊耳的应用范围较广，经常会遇见需要重新设计吊耳但规范上又没有的情况，许多人员对其在强度上的校核存在着方法上的严重错误，虽然到目前为止还没有产生过大的意外，但却是危及吊装安全的潜在隐患。本文主要论述耳板式吊耳本体在设计受力方向上的受力分析和设计原理，对吊耳焊缝的强度验算不再赘述。

1 问题的提出

在实际工作中经常会出现以下情况，给吊装安全带来潜在隐患。

（1）有的技术人员对所设计的耳板式吊耳的验算方法为：将吊耳受力简单的理解为单纯的受拉过程，仅仅校核吊耳危险断面的拉应力，甚至于根本不考虑耳孔的承压应力。

（2）耳板式吊耳设计时对耳孔的要求应该是机加工，这就对耳孔的表面加工精度有一定的要求，而实际工作中，施工人员往往从加工成本考虑，经常用火焊切割的方法代替机加工。

（3）吊装时，所采用吊轴或卸扣轴的直径小于耳板式吊耳的耳孔直径往往很多，这会导致耳板的受力更为复杂。

2 理论分析

我们举例来说明，如图1所示，假设P=20t，B=210mm，R1=105mm，c=25mm，r=42mm，材料为A3钢，同时假设销轴与吊耳孔为间隙配合，根据此条件求解危险截面的应力。

图1 耳板式吊耳示意图

2.1 存在问题的计算方式

按照我们部分技术人员通常的验算方法为：

取动载系数k=1.1（吊立过程取k=1.1，水平吊运过程取k=1.30），对危险截面A—A，则应力为：

因为有σ=69.8MPa＜[σ]=180MPa

故通常我们的技术人员仅根据此就判断该吊耳可以安全使用，甚至都不考虑耳孔的承压应力。现在我们再来对其销孔的承压应力进行验算：

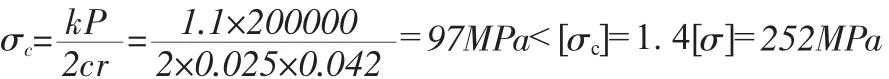
根据计算结果可知：虽然该例中的承压应力计算为合格，但其值σc却是大于σ的；而且从σ、σc的计算公式中我们可以看到：假如销轴的的材料强度足够大，使其只需较小的r就能承受20t的载荷，我们可以发现此时σ的值会变小，而σc值则会变大，完全有可能超过其承压许用应力值[σc]，从而导致吊耳材料的失效而发生事故。所以且不说平常我们技术人员验算耳板强度的方法正确与否，但就其根本不考虑耳孔的承压强度问题是绝不可行的。

2.2 力学分析

图2 耳板式吊耳力学分析图

实际上吊耳板的受力状态较以上复杂得多，决不是简单的计算就可以的。如图2所示，我们仍然假设销轴与吊耳孔为间隙配合，应该首先根据吊耳板承受的最大拉力P求出危险截面（图中的水平截面b-b，垂直截面a-a）上的内力，然后引入弹性曲梁公式求出相应的内力，并进行强度校核。

2.2.1 内力计算

吊耳板承受的拉力P通过耳孔（销轴孔）壁以沿弧长分布压力p的形式传递给销轴，其沿弧长方向按照正旋规律分布，即

如图2所示：根据耳板的平衡条件可知

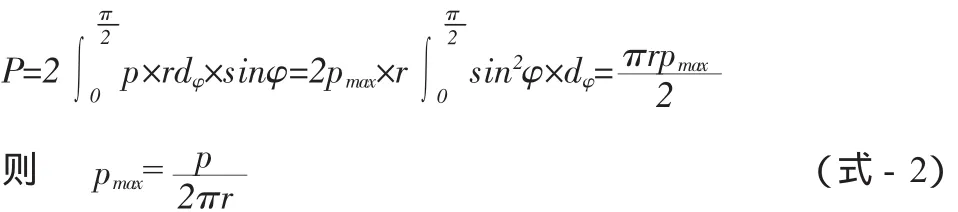
根据耳板结构和受力的对称性，可知耳板上反对称的内力（即剪力）等于零。若沿销孔中心线水平截开耳板，则截面上只有轴力Nb及弯矩Mb，如图3所示。

同时由于根据平衡方程解不出弯矩Mb，所以该求解成为一次超静定问题，须根据耳板的变形条件求解Mb。为此需列出与水平线成α角的任意截面的弯矩方程：

同样因为耳板的结构和受力是对称的，故转角θα应该等于零，即

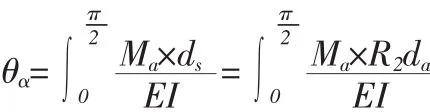
将（式-4）代入上式，得

将

（式-6）代入（式-5）可得

同样由图3，根据平衡条件∑X=0，得

2.2.2 强度验算

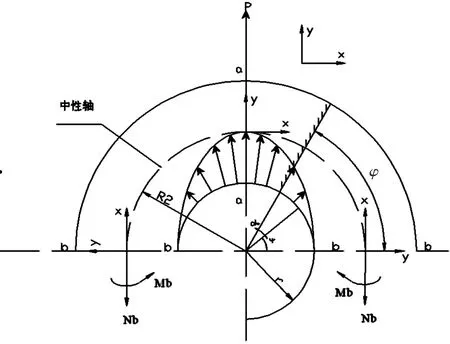
图3 截面受力分析图

根据弹性曲梁公式来求解危险截面的应力，如图3所示。对应于每个危险截面的座标系原点均在其相应的中性轴上，并且外侧方向为y轴正方向。于是有任一截面的应力值为

式中：A为计算截面积，对于矩形面积有A=(R1-r)×c=h×c

K位于计算界面形状有关的系数，对于矩形面积有

同时引入动载系数k=1.1，即将上述各式中的P值全部以kP(1.1P)代替。

对于b—b截面：

回头我们再来看前面举的实例，将P=20t，R1=105mm，c=25mm，r=42mm，R2=73.5mm，h=63mm分别代入上述（式-10）、（式-12）、（式-13）、（式-15）、（式-16），可分别得到

根据以上结果我们画出耳板危险截面的应力分布图，如图4所示。

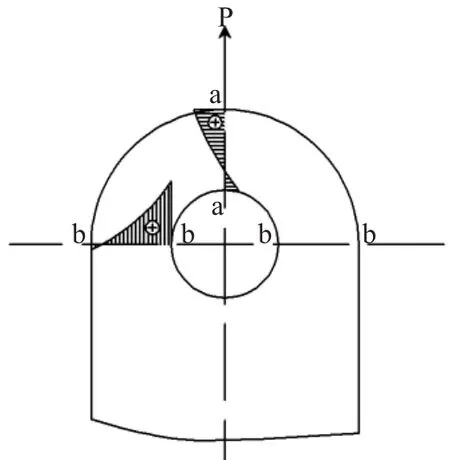
图4 应力分布图

比较两种方法计算出来的结果，很明显根据弹性曲梁公式得到的最大应力结果不但远大于第一种方法得出的结果，甚至有b—b截面内侧的应力值为200.8超过180百分之十几，即b—b截面内侧的应力值超过材料的许用应力值，从而完全可能导致耳板材料的强度实效，如将此耳板用于实际的吊装工程中，则会导致严重的安全生产事故，结果将不可想象。

3 分析结论

针对前面所提的问题以及耳板式吊耳的受力分析和实例计算结果的对比，我们可以得出如下应该注意的问题：

（1）耳板式吊耳设计时，必须要对其承压应力进行校核，同时必须引入动载系数；

（2）耳板式吊耳设计校核时，应对耳板的受力状态和应力分布要有清晰地认识，采用正确的方法对其强度进行校核；这样才能有针对性地解决问题。比如上例中，从图4我们可知，耳板式吊耳的最大应力值出现在与受力方向垂直的危险截面内侧，对于该例，我们并不一定非要将整块吊耳板全部更换，而可以在耳孔两侧贴加强板的方式来解决问题，避免材料的浪费。这种解决方式同时也提醒我们技术人员在实际进行吊耳设计时，尽量考虑选用现有的材料，通过较薄板的合理组合来替代厚板的使用，可以达到节约材料成本的目的；

（3）耳孔的精度问题。我们都知道，材料表面的精度对材料的强度是有很大的影响的。用火焰切割出来的耳孔表面高低不平，使得轴与耳孔的接触由设计要求的面接触变为实际上的点接触，从而改变整个受力形式，使其承压应力成倍增加，结果可能导致材料的失效。同时由于表面高低不平，更会导致应力的集中，从而使设计本合格的耳板在集中应力的作用下发生失效；

（4）现场使用的吊轴与耳孔不配套，同样也会导致承压应力增加和拉应力数值的改变，在上述分析中我们都基于这样的一个假设：假设销轴与吊耳孔为间隙配合，也就是吊轴直径与耳孔直径几乎是一样的，但实际的吊装过程不可能达到此要求，所以在设计时还必须引入载荷分布系数，一般取1.35，这样承压应力和两个危险截面的应力表述公式分别为：

实际设计校核时只需核算（式-17）、（式-18）、（式-21）即可。

4 结束语

通过对耳板式吊耳的受力和强度校核方法进行材料力学和弹性理学的理论性分析，指出了部分工程技术人员设计吊耳时的不足与失误，给出了实际工程应用耳板式吊耳的校核方法，为在设计与施工中提供了有益的参考。

1刘鸿文.材料力学.高等教育出版社

2杨长马癸.金属结构.机械工业出版社

3吴家龙.弹性力学.高等教育出版社

book=62,ebook=51

TU602

B

1672-9323（2010）03-0062-03

2010-01-12）