三角网格模型特征线提取方法

上官宁,刘斌

(华侨大学机电及自动化学院,福建泉州362021)

三角网格模型特征线提取方法

上官宁,刘斌

(华侨大学机电及自动化学院,福建泉州362021)

提出一种三角网格模型的特征线提取方法.在三角网格模型特征点提取的基础上,人工交互地指定初始特征点.由初始特征点开始,应用主成分分析法分析特定范围内特征点集的主方向,寻找主方向上距离质心最远的特征点,并作为特征方向上的后继特征点;依次迭代,顺序记录特征点序列,直至寻找的后继特征点落回到初始特征域内才结束.最终,用3次非均匀B样条曲线,将得到的特征点集合拟合生成光滑特征线.

三角网格模型;特征线;提取;主成分分析;主曲率

在反求工程、计算机动画、计算机可视化等领域,对网格模型进行CAD模型重建、网格简化、网格光顺、网格变形及网格编辑等处理过程中,通常希望能够保留模型的特征.更为实际的是,三角网格模型被广泛地应用于表达任意形状和拓扑的三维几何模型.现有的网格模型特征线提取方法,一般是先找出网格上曲率突变点作为特征点,然后,将这些离散的特征点连接成线,也就是特征线.典型的代表有M ilroy等[1]在OCS(Orthogonal Cross Section)模型的基础上,估算出模型上各点处的法矢,利用法矢和邻点信息拟合一张二次曲面,计算该二次曲面的主曲率和主方向,主曲率在主方向的极值点被确定为特征点;然后,用能量最小化原则将特征点连成样条线.Yang等[2]通过建立局部参数二次曲面来计算主曲率和主方向,实现了对密集数据点云的特征线提取.该方法对有误差影响的点云或稀疏点云不适用.刘胜兰等[3]提出,根据相邻三角片的法矢夹角和各点主曲率是否为极值,分两次提取特征点,利用三角顶点加权和均匀化等方法,减少狭长三角片对特征点提取的计算误差影响;然后,将特征点分组连接成B样条曲线,实现了三角网格模型的特征线提取.郭延文等[4]提出半自动化特征线提取技术,根据用户指定的点集,考虑两点间的距离和方向及曲率信息,提取出初始特征区域后,再将特征区域映射至二维平面.最后,运用Snake算法精炼后映射回三维空间,得出平滑特征线.这些方法对于离散的网格模型的特征点提取已很成熟,然而,将这些特征点连接生成特征线的过程都存在弊端,因此并不能很好地将特征点分组连接.为此,本文着重研究三角网格模型的特征线提取.

1 特征点提取

三角网格模型的特征线生成算法是,采用主曲率极值法来判断提取出模型的特征顶点.

1.1 离散网格顶点法矢计算

三角网格模型是离散的,不同于连续表面.采用文[5]从力学角度提出的单位法矢加权叠加公式,计算模型中网格顶点法矢.如图1所示,对于三角网格模型中的任一点Vi,设Vi的m个相关三角形为Tk(1≤k≤m).相应地,Vi有m个相邻顶点Pk(1≤k≤m),Ni为顶点Vi处的法矢,nk为Tk向外的单位法矢,di,k为Vi与Pk的距离.则有

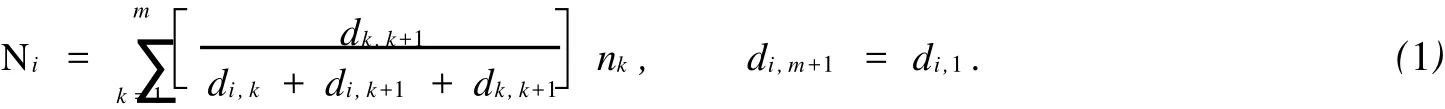
1.2 主曲率和主方向的计算

由曲面论可知,零件的棱线、脊线、曲面交线等处曲面的曲率较大.为计算每一顶点的曲率,可在顶点P处建立曲面S(u,v)=(u,v,h(u,v)),如图2所示.其中:h(u,v)=au2+buv+cv2局部坐标系(Phuv)由绝对坐标(Oxyz)经变换可得,即经O平移至P,再旋转使得z轴与h轴重合,此时u,v可取x,y轴.

建立的曲面在P点处存在无数条主法矢和曲面的法矢N重合的曲线,该曲线族的曲率k是曲面在P点的法曲率.法曲率中的极小值k1和极大值k2称为主曲率,k1,k2对应的曲线的切线方向分别为m1, m2,称为主方向,两者总是互相垂直.

由式(1)可以求出任一点Vi的法矢Ni,然后,在Vi处建立二次曲面S(u,v),且Vi点的邻接点Vj(1≤j≤m)在局部坐标系(Phuv)下的坐标值为(uj,vj,hj).由m个邻点得到的线性方程组为

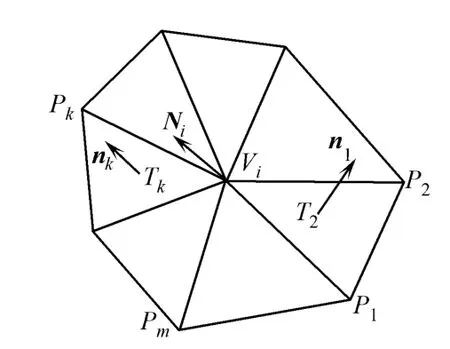
图1 Vi点的法矢Fig.1 No rmal vector of vertex Vi

图2 P点的局部坐标系Fig.2 Local coo rdinate system of point P

用最小二乘法解此方程组,即可求得曲面S(u,v).方程的最小二乘解就是使得各个邻点到曲面距离的平方和最小时的解.由曲面的第一、第二基本公式,可得到曲面上Vi处的法曲率k,即

其中:λ=d u/d v;d k(λ)/dλ=0的根为λ1,λ2.此时,法曲率k就达到它的极值k1,k2,对应的主方向为(1, λ1),(1,λ2);或者为(-λ1,1),(-λ2,1).对于曲面S(u,v),k1,k2值分别为

图3 极值点判断示意图Fig.3 Schematic of determination of extremum point

1.3 主曲率极值判断

在计算出各顶点的主曲率后,可通过对主曲率的极值判断得出特征点集.具体方法如图3所示.

对任意顶点Vi,在m1方向及其反向的延长线与三角形的交点为A,B (实际空间上并不相交,是延长线在三角面上的垂直投影与三角形的交点).当Vi点主曲率k1的绝对值大于A,B两点在m1方向上的k值的绝对值时,则Vi点就是在m1方向上的曲率极值点,标示为特征点.A,B点的k值可由Vj,Vj+1在m1方向上的k1值线性组合求得.该方法同样适用于k2,可判断Pi在方向m2是否为特征点.

需要说明的是,由于存在曲率计算误差,直接根据上述极值判断的特征点远远多于实际所需.引入文[3]中的办法,加入局部和整体误差消除因子.

(1)加入局部误差消除因子Ierr.在比较极值时,用(1-Ierr)×k1来代替k1,用(1-Ierr)×k2来代替k2,即Vi点主曲率极值比A,B点的k值大到一定程度时,才认为该点是特征点.Ierr可使特征点密集的区域稀疏化,可根据实际情况取值.为了增强大曲率区域的影响,给每一极值点赋一个曲率权值.权值等于主曲率极值的绝对值,若主曲率在两个方向上均为极值,则取极值的绝对值之和.

(2)加入整体误差阈值gerr.对于每一个曲率极值点,当某一点曲率权值与最大曲率权值的比值小于阈值gerr时,则将这一点从特征点序列中去掉,即利用gerr可以去掉曲率平坦区域的杂点.

图4 鞋楦模型及其特征点提取Fig.4 Shoe lastmodel and the extraction of its feature points

对鞋楦三角网格模型进行特征点提取,如图4所示.图4中:网格顶点数为18 064;提取的特征点数为3 824;Ierr取0.008;gerr取所有主曲率极值的绝对平均值的0.05%.

2 特征线生成

把已提取出的所有特征点看作一个特征点集F,集合中特征点的排列是无序的,且存在某些杂点或不是主要关注的特征点.如图4中鞋楦模型的特征点中,主要关注的是统口线和楦底板线这两条特征线的识别.提出一种基于主成分分析技术(PCA),将无序的特征点集有针对性的分组连接,由用户指定需要提取的初始特征位置的特征线生成算法.

2.1 主特征方向识别

特征线生成的第1步,是要将无序的特征点集有序化,形成一串沿特征方向行进的特征点序列,而其首要任务就是识别主特征方向.

对于特征点P∈F,P点在其δ邻域内的特征点集合为N(P)={pi∈F||pi-P|≤δ},i=1,…,k.然后,应用PCA方法,对N(p)进行主成分分析.让集合N(P)中的任一点pi减去集合中所有点的平均坐标¯p(即质心坐标),计算协方差矩阵C(3,3)为

对协方差矩阵进行特征分解,求解特征方程

则最大特征值λ0所对应的最大特征向量x0为特征点集合的第一主方向,即是所求的主特征方向.

图5 不同δ邻域的主特征方向识别Fig.5 Identification of p rimary feature direction in differentδneighbo rhoods

特别需要注意的是,δ邻域大小的选取会影响主特征方向识别的准确性,尤其是特征点在局部分布不均匀的情况下.在δ邻域选取不同大小时,对主特征方向识别的比较,如图5所示.图5中:虚线圆圈表示选取的δ大小;直线段为识别的主特征方向.

文[6]中提出了一种自适应地选取δ大小的方法,逐步递增δ值来计算主方向.即将邻域内的点投影至主方向上,得到二维点集,其X坐标与Y坐标集合对应两个随机变量,并计算相关系数ρ(X,Y).根据线性相关性,直至|ρ|≥0.7时,选取的δ为较好的值.

2.2 特征线生成

由用户指定初始特征点后,就可由初始特征点开始进行特征点排序.

首先,以初始特征点为中心,进行主特征方向识别.应用PCA方法提取初始特征域内的主特征方向线后,将初始特征域内的所有特征点投影至主特征方向线上,取出距离质心最远的特征点,作为后继特征点加入特征点序列,且记录初始特征点至该后继特征点的方向为特征线的行进方向.

其次,再以刚求出的后继特征点为中心,进入下一轮的主特征方向提取.

重复以上步骤,寻找又一后继特征点.如此迭代,直至寻找的后继特征点落回到初始特征域内才结束.最终,可得到一串有序的特征点集合,用3次非均匀B样条曲线拟合生成光滑特征线.

所提算法已用Visual C++语言和OpenGL技术在微机上编程实现.鞋楦统口特征线提取的步骤示例,如图6所示.

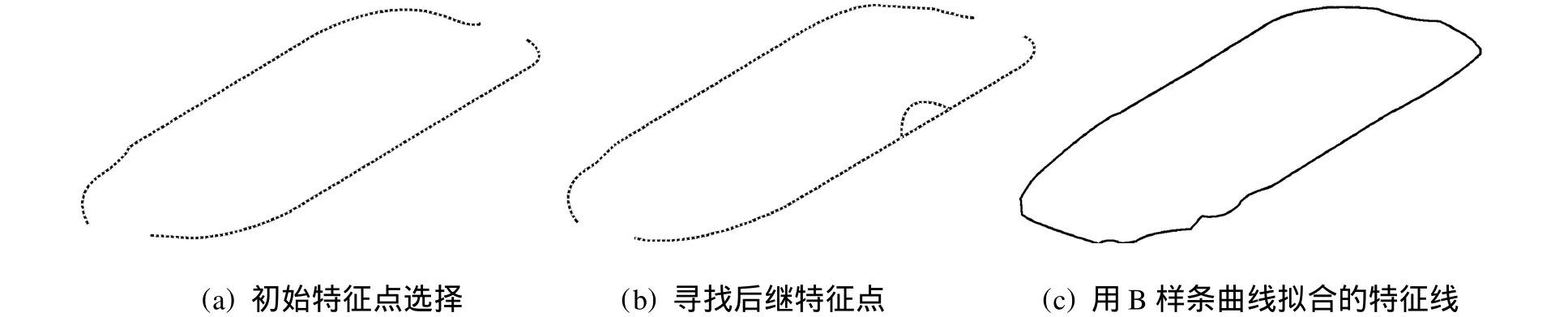
图6 鞋楦模型统口特征线生成Fig.6 Feature line generation of mouth system of shoe lastmodel

3 结束语

在特征点提取的基础上,提出应用主成分分析的方法识别主特征方向.沿特征点生长方向搜寻后继特征点,达到将无序特征点有序化的目的,进而实现了网格模型的特征线提取.通过用户交互式的选取初始特征点,可更针对性地进行有用特征线的提取,比自动提取方法更具实用价值.

[1] M ILROY M J,BRADLEY C,V ICKERS GW.Segmentation of a w raparound model using an active contour[J]. Computer Aided Design,1997,29(4):299-320.

[2] YANGM,LEE E.Segmentation of measured point data using a parametric quadric surface app roximation[J].Computer Aided Design,1999,31(7):449-457.

[3] 刘胜兰,周儒荣,张丽艳.三角网格模型的特征线提取[J].计算机辅助设计与图形学学报,2003,15(4):445-448.

[4] GUO Yan-wen,PENGQun-sheng,HU Guo-fei,et al.Smooth feature line detection fo r meshes[J].Journal of Zhejiang University:Science(A),2005,6(5):460-468.

[5] 柯映林.离散数据的几何造型技术及其应用研究[D].南京:南京航空航天大学,1992.

[6] DAN IELSJⅡ,HA L K,OCHOTTA T,et al.Robust smoo th feature extraction from point clouds[C]∥Proceedings of the IEEE International Conference on Shape Modeling and App lications.Washington D C:IEEE Computer Society,2007:123-136.

SHANG-GUAN Ning,L IU Bin
(College of Mechanical Engineering and Automation,Huaqiao University,Quanzhou 362021,China)

A method of feature line extraction from triangular mesh model is p resented.Initial feature point ismanually specified based on feature points extraction from triangularmesh model.From the beginning of initial feature point,method of p rincip le component analysis(PCA)is used to analyze p rimary direction of feature points in a special region and to search the feature pointw hich is farthest from the center ofmass in the p rimary direction and w ill be chosen as subsequent feature point.Iteratively,the sequence of the feature points is reco rded in order until the sought subsequent feature points are among the initial feature region.Finally,third-o rder non-uniform rational B-spline curve is used and that obtained set of feature points is fit into a smooth feature line.

triangular mesh model;feature line;extraction;p rincipal component analysis;p rincip le curvature

Investigation of Feature L ine Extraction from Triangular Mesh M odel

TP 391.41

A

(责任编辑:陈志贤 英文审校:郑亚青)

1000-5013(2010)05-0487-04

2009-07-04

刘斌(1972-),男,副教授,主要从事材料成型数值模拟的研究.E-mail:mold_bin@hqu.edu.cn.

福建省科技计划重点项目(2006H0029);福建省自然科学基金资助项目(E0710017,E0810040)