适用于数值流形法分析的混凝土徐变递推公式
林绍忠,明峥嵘(.长江科学院非连续变形分析实验室,武汉 43000;.北京博奇电力科技有限公司武汉分公司,武汉 43007)
适用于数值流形法分析的混凝土徐变递推公式
林绍忠1,明峥嵘2
(1.长江科学院非连续变形分析实验室,武汉 430010;2.北京博奇电力科技有限公司武汉分公司,武汉 430071)
目前大体积混凝土结构温度应力仿真计算主要采用有限元法。对于复杂结构,有限元法仿真计算存在计算规模大、前处理难度大等问题。数值流形法具有网格剖分和自适应分析方便等优点,可为温度应力仿真计算提供有力的分析手段。混凝土徐变可以松驰温度应力,在温度应力仿真计算中一般都要考虑徐变的影响。有限元法中采用的徐变递推公式是基于数值积分点的应力状态,但数值流形法的单元应力呈多项式函数分布,这种递推公式已不适用。为此,推导了适合于数值流形法的徐变递推公式及等效荷载计算公式,并编制了数值流形法仿真计算程序,通过数值算例验证了公式的正确性。
数值流形法;混凝土结构;徐变递推公式;温度应力;仿真计算
1 概 述
数值流形法[1](简称流形法)是石根华博士提出的一种新的数值计算方法。该方法采用2套相互独立的网格——反映数值解精度的数学网格和反映几何边界和材料分区的物理网格,将研究区域划分成有限个相互重叠的集合(称为物理覆盖),在各个覆盖上独立定义局部覆盖函数,通过权函数加权平均得到整个求解域上的总体函数。由于数学网格和物理网格的相互独立性,可以采用规则的数学网格对物理区域进行切分形成流形元,这种切分过程只涉及相对简单的几何运算,速度比较快。覆盖函数可以是多项式或级数形式,随着阶数的提高或级数项的增加,精度得以提高,自适应分析方便。和有限元一样,流形元是基本的计算单元,但可具有更复杂的形状。鉴于流形法所具有的优点,文献[2]将其应用于大体积混凝土结构的温度场及温度应力仿真计算,但没有考虑混凝土徐变的影响。混凝土是徐变体,考虑徐变后,温度应力得到松弛,因此在温度应力仿真计算中一般都要考虑混凝土徐变的影响。但目前有限元法中采用的徐变递推公式是基于数值积分点的应力状态,而流形法多采用单纯形积分进行精确积分,其单元应力呈多项式函数分布,这种递推公式已不再适用,需要重新推导。
2 流形元位移函数和温度函数
2.1 覆盖函数
目前,流形法一般采用有限元网格作为数学网格。覆盖函数定义在数学网格的结点上,类似于有限元的结点位移,但可以是常数、多项式函数或其它形式级数。覆盖函数与物理边界无关,如果物体只占数学网格的一部分,覆盖函数仍然是相同的。设定义在物理覆盖上的覆盖函数为多项式函数,
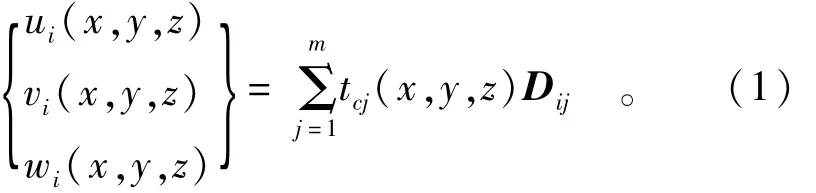
式中:Dij={uij,vij,wij}T为覆盖函数的系数(广义位移);tcj(x,y,z)是多项式基底,如1,x,y,z等。对于完全N阶覆盖函数,项数m=(N+1)(N+2)(N+3)/6。传统有限元法中,结点位移ui,vi,wi是常量,即采用0阶覆盖函数。
2.2 单元位移函数
设流形元e是n个物理覆盖的交集,则该单元的位移函数为
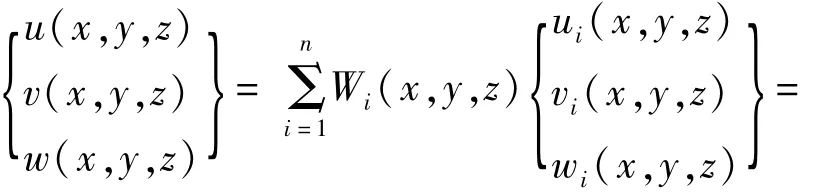
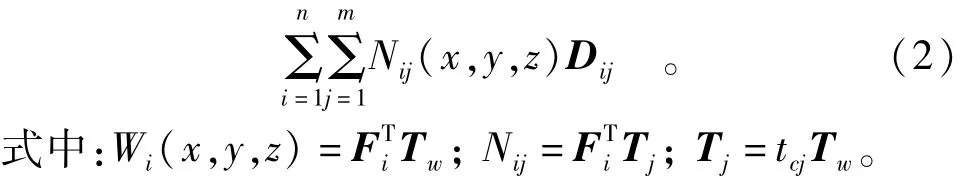
以上公式中,Wi为权函数,Fi是其系数列阵,Tw是多项式基底集。采用有限元网格作为数学网格时,Wi即是有限元的形函数,n为有限元的结点数。流形法中数学网格与物理网格不要求重合,因此可以采用形态简单的有限元来构造显式权函数,如平面的三角形单元、矩形单元和三维的四面体单元和长方体单元。

2.3 单元温度函数
与位移函数的定义一样,在物理覆盖Ci上的温度覆盖函数为多项式函数,
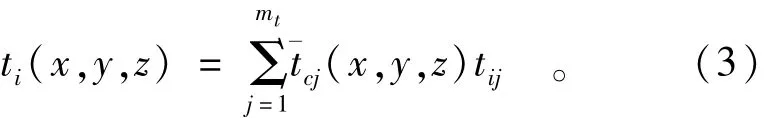
式中:tij为待定系数;珋tcj(x,y,z)为多项式基底集;mt为温度场覆盖函数多项式的项数。在计算温度应力时,可采用相同的数学网格,位移场和温度场覆盖函数阶数可不一样,但位移场覆盖函数的阶数必须不低于温度场的阶数。
同理,单元内的温度场可表示为

3 混凝土徐变递推公式
3.1 混凝土增量应力应变关系

3.2 徐变递推公式
混凝土徐变度可表示为

4 温度和徐变等效荷载
文献[2]给出了温度等效荷载公式,文献[3]给出了初应变等效荷载的一般公式。这里给出同时考虑温度和徐变的等效荷载公式。初应变表达式为
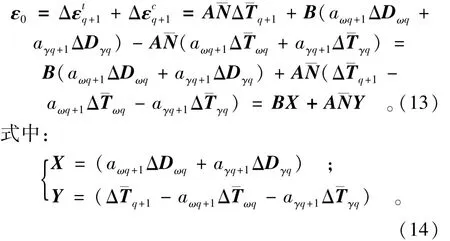
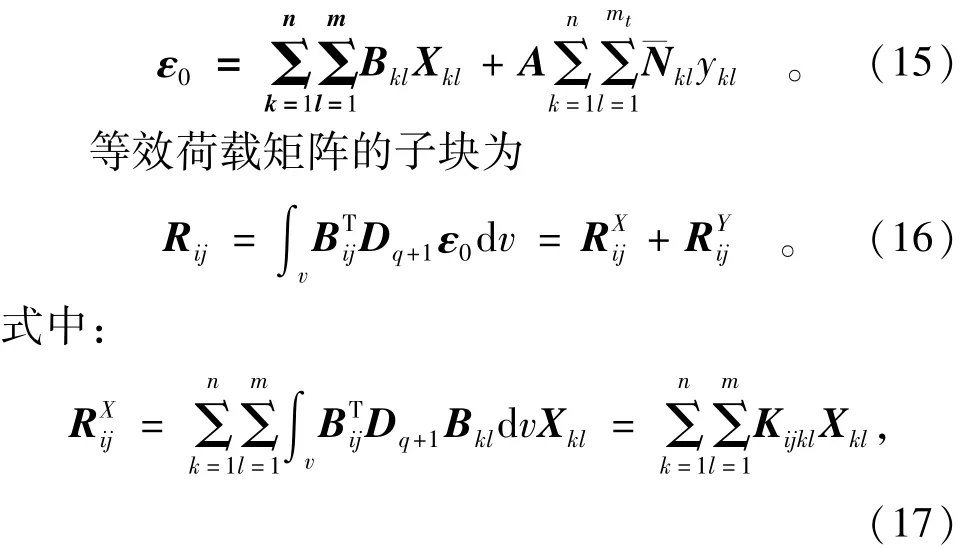
Kijkl为流形元刚度矩阵的子块,见文[3];
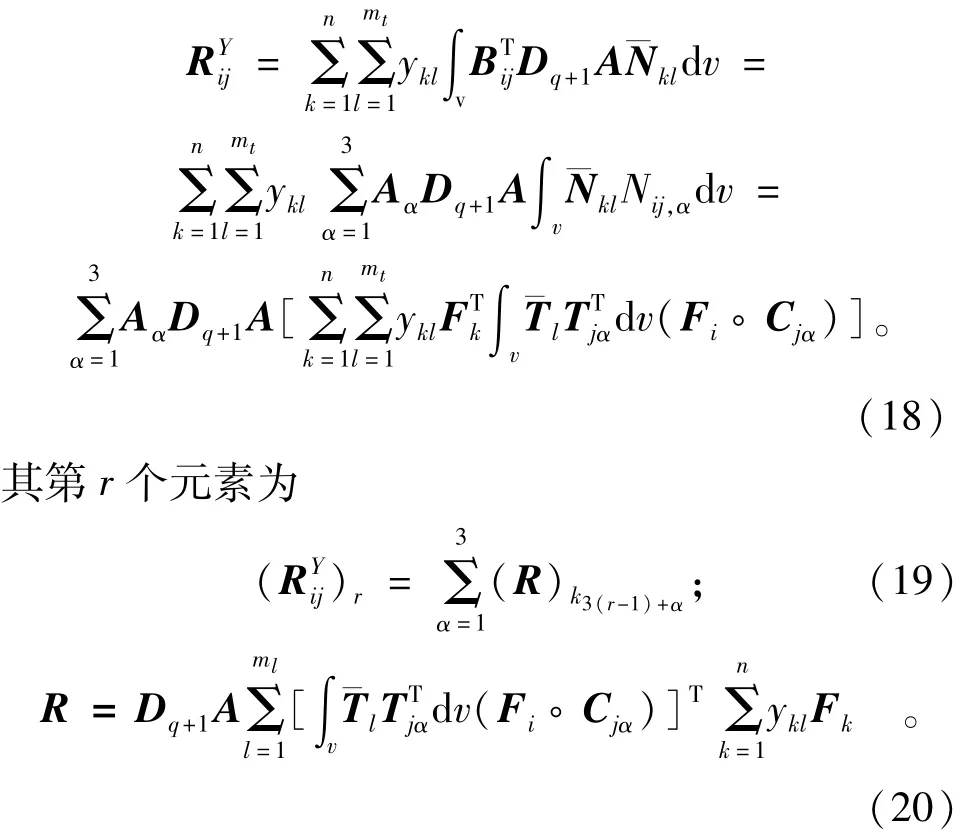
式(20)中的被积函数为多项式基底的乘积,可以直接用单纯形积分法[4]进行精确积分。
5 算 例
如图1,混凝土块体平面尺寸为20 m×20 m,底面基岩约束。分两层浇筑,每层厚0.5 m,间隙期7 d,顶面为气温边界,其他边界为绝热边界。在混凝土水化热温升和环境温度作用下,同时考虑徐变影响,计算温度应力。每个浇筑层为一流形元,见图2。作为比较,用有限元法进行计算,每个浇筑块划分为5层单元,见图3。A,B 2点(见图1)应力计算结果见表1。可以看出,在较粗的数学网格情况下,流形法通过提高覆盖函数的阶数可获得迅速逼近细网格的有限元解,在1阶时已取得了较好的精度。

图1 混凝土块Fig.1 A concrete block in the test
图2 流形元网格Fig.2 Manifold elementmesh

图3 有限元网格Fig.3 Finite elementmesh
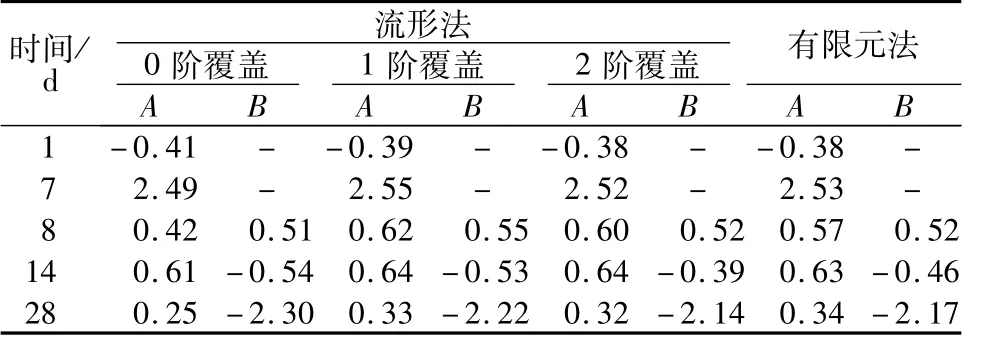
表1 A,B点应力σyTable 1 Stressσyat point A and B MPa
6 结 语
流形法具有网格剖分和自适应分析方便等优点,为大体积混凝土结构温度应力仿真计算提供了有力的分析手段。为考虑徐变影响,本文推导了适用于流形法分析的徐变递推公式及等效荷载公式。算例验证了这些公式的正确性。至此,笔者开发的高阶流形法计算程序已可用于大体积混凝土结构温度场和温度应力仿真计算,其中可以考虑常规荷载作用和混凝土徐变的影响。
[1] 石根华.数值流形方法与非连续变形分析[M].裴觉民,译.北京:清华大学出版社,1997.(SHIGenhua.Numerical Manifold Method and Discontinuous DeformationAnalysis[M].Translated by Pei Juemin.Beijing:Tsinghua University Press,1997.(in Chinese))
[2] 林绍忠,明峥嵘,祁勇峰.用数值流形法分析温度场及温度应力[J].长江科学院院报,2007,24(5):72-75.(LIN Shaozhong,MING Zhengrong,QI Yongfeng.Thermal field and thermal stress analysis based on numericalmanifold Method[J].Journal of Yangtze River Scientific Research institute,2007,24(5):72-75.(in Chinese))
[3] 林绍忠,祁勇峰,苏海东.基于矩阵特殊运算的高阶流形元单元分析[J].长江科学院院报,2006,23(3):36-39.
(LIN Shaozhong,QI Yongfeng,SU Haidong.Element analysis of highorder numericalmanifold method based on specialmatrix operations[J].Journal of Yangtze River Scientific Research Institute,2006,23(3):36-39.(in Chinese))
[4] 林绍忠.单纯形积分的递推公式[J].长江科学院院报.2005,22(3):32-34.(LIN Shaozhong.Recursive formula for simplex integration[J].Journal of Yangtze River Scientific Research Institute,2005,22(3):32-34.(in Chinese) )
(编辑:周晓雁)
Recursive Formulae of Concrete Creep Suitable for Numerical M anifold M ethod Analysis
LIN Shaozhong1,MING Zhengrong2
(1.DDA Center,Yangtze River Scientific Research Institute,Wuhan 430010,China;2.Wuhan Branch of Beijing Bootes Electric Power Science&Technology CO.,LTD.,Wuhan 430071,China)
Currently,the thermal stress analysis simulating the construction process ofmass concrete structures primarily adopts the finite elementmethod(FEM).Butmuch computation is required and difficulties inmesh generation are encountered in conducting FEM analysis of complicated structures.For convenience in adaptive analysis and mesh division,the numericalmanifoldmethod(NMM)provides a new effective approach for the thermal stress analysis.The effects of the concrete creep should be generally considered in the thermal stress analysis as the concrete creep can reduce thermal stresses.The recursive formulae of the concrete creep widely used in FEM,which were derived based on the stresses at numerically integrated points of finite elements,are not suitable for NMM analysis due to the stresses of manifold elements are expressed in the polynomial form,especially in highorder NMM.According to the recursive formulae of concrete creep used in FEM,recursive formulae of concrete creep and formulae of corresponding equivalent loads suitable for NMM analysis are deduced.On the basis of the derived formulae,a program of highorder NMM for the thermal field and the thermal stress analysis is developed and verified by an example.
NMM;mass concrete structure;recursive formulae of creep;thermal stress;simulation analysis
TV315;O242
A
1001-5485(2010)07-0056-04
20090915
林绍忠(1960),男,福建福安人,教授级高级工程师,工学博士,主要从事水工结构数值分析研究,(电话)02782820007(电子信箱)Linsz@mail.crsri.cn。

