蓄滞洪区洪水调度优化研究

刘 云，李义天，谈广鸣，邓金运，孙昭华，寇继生（．长江大学石油工程学院“油气钻采工程”湖北省重点实验室，湖北荆州 440；．武汉大学水资源与水电工程科学国家重点实验室，武汉 4007；．上海大学数学系，上海 00444）

蓄滞洪区洪水调度优化研究

刘 云1，李义天2，谈广鸣2，邓金运2，孙昭华2，寇继生3
（1．长江大学石油工程学院“油气钻采工程”湖北省重点实验室，湖北荆州 434023；2．武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；3．上海大学数学系，上海 200444）

针对洪水调度中影响因素众多且有不确定性因素的特点，引入多目标模糊优选理论和方法，建立了蓄滞洪区洪水调度方案模糊优选模型。并将此模型应用于实际洪水调度中，有效地解决了受确定性因素和不确定性因素影响的蓄滞洪区洪水调度方案的多目标优化决策问题。

蓄滞洪区；洪水调度；模糊优选

1 概 述

蓄滞洪区作为水利工程的重要组成部分，在减轻沿岸大堤的洪水压力等方面起到了重要作用。蓄滞洪区经济的发展不仅导致分洪损失上升，而且制约着蓄滞洪区的运用。蓄滞洪区既是防洪工程手段，又是减灾对象。所以，在确保重点地区安全的同时，有必要通过优化理论选择蓄滞洪区洪水调度方案，尽量减少由开启蓄滞洪区带来的损失。

对于多个蓄滞洪区洪水调度这个全局优化问题，任意改变局部，都会影响全局，其复杂程度可想而知。建国后，在经历多次扒口实践后，对扒口分洪积累了许多宝贵经验，为进一步提高运用效果，还进行了一系列科学试验。主要包括：土堤爆破试验确定单位爆破土堤的用药量；扒口水流交汊试验；口门位置选择效果分析等［1］。倪晋仁等人对洪湖分蓄洪工程存在的问题、特大洪水条件下分洪区启用时的口门位置及其分洪区启用前后的有关重要问题进行探讨，提出了相应对策［2］。何琦对淮河蒙洼蓄洪区开启时机进行了研究［3］。要威对多个蓄滞洪区联合调度开启时机和开启方式进行了优化［4］。但是，这些研究主要对蓄滞洪区口门位置、开启时机、开启方式等进行了研究，对蓄滞洪区运用后经济损失、生态环境等进行分析研究比较少。

本文引入多目标模糊优选理论和方法［5，6］，综合考虑经济损失和生态环境等定量和定性目标，建立了蓄滞洪区洪水调度方案模糊优选模型，从而能融入人的知识经验，使决策者直接参与其中，并能够考虑多目标中各目标的重要程度，而且能够量化定性目标，使定性目标与定量目标一并参与决策，使决策更科学。

2 蓄滞洪区洪水调度方案模糊优选模型

蓄滞洪区洪水调度研究涉及的方案、目标多，可归属于在多目标决策系统中，既有定量目标（目标特征值可以直接定量或量化），又有难于直接量化的定性目标的决策优选问题。

2．1 蓄滞洪区调度方案定量目标计算

2．1．1 蓄滞洪区蓄量计算

式中：w为蓄滞洪区蓄洪量；Q为蓄滞洪区口门流量；T为蓄滞洪区时间。

2．1．2 蓄滞洪区洪灾经济损失计算

洪水灾害损失评估，国内外已有较多的研究，但基本方法变化不大。由于影响损失评估的因素很多，各地区的经济情况差异很大，目前尚没有综合预测洪水灾害损失的方法，较为通用的方法仍然是采用经验曲线法，比如建立水深－损失曲线。

社会经济资料和蓄滞洪区自然灾害指标的资料获取，是进行损失评估的基础，也是进行灾害损失评估的重要一环。在洪水灾害损失计算中用到的自然评估，主要有水深、流速、淹没历时、蓄洪量等资料。这些资料的获取可通过调查以往实际洪水过程得到，或通过遥感技术来测定，或数学模拟的方法来得到。这些资料都存储在数据库Access中，数据库资料随时可以更新，是洪水实时损失评价的理想数据源。

根据半结构性决策系统模糊优选理论与模型，对于每一个定量或者定性目标不同方案的比较，最后都要转化为相对优属度矩阵，并归一化。蓄滞洪区经济损失采用回归模型，建立如下函数关系式式中：n为蓄滞洪区主要控制站水位过程线超过控制水位的次数；t1和t2为每次超过控制水位的起、止时间。

2．2 蓄滞洪区调度方案定性目标分析

蓄滞洪区洪水调度涉及生态环境等方面的因素。蓄滞洪区洪水调度由于涉及面广，环境问题多，各种因素交织在一起，环评工作难度大，只作定性分析。蓄滞洪区洪水调度对环境的主要不利影响为：需迁移人口，农田淹没，村庄淹没，房屋倒塌，水利工程设施被冲毁，公路和供电设施等全部中断等。

各蓄滞洪区调度方案环境优劣难于详细分析，仅以迁移人口为主要评价因素，迁移人口越少的方案越优。

2．3 计算步骤

2．3．1 求各定量目标（K个）、各方案对优的相对隶属度

对于第i目标（i＝1，2，…，K），分别求第j个方案（j＝1，2，…，n）的相对隶属度rij。

其中，对于越大越优目标（效益型）

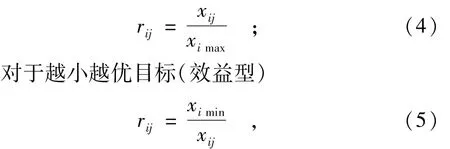
式中：E为经济损失；w为蓄滞洪区蓄洪量。

2．1．3 蓄滞洪区分洪效果

当蓄滞洪区主要控制站附近区出现超额洪量时，就需要根据实时洪水组成情况，相机决定分洪运用次序及应采取的措施，总的目标是把可能受灾的损失降到最低点。所以，当现状水位条件下尚不能承纳超额水量时，就需启用蓄滞洪区来减少蓄滞洪区主要控制站附近区超额水量，从而降低河道水位，使控制站水位限制在防御水位之内。

评价蓄滞洪区分洪效果，就以蓄滞洪区主要控制站的水位超过控制水位的时间作为标准，时间越短，分洪效果越好。

蓄滞洪区蓄量、蓄滞洪区洪灾经济损失、蓄滞洪区分洪效果3个定量目标都是越小越好，故都用式（5）计算。

2．3．2 求各定性目标（m－k）个，各方案对优的相对隶属度

对于第i个目标（i＝k＋1，…，m）：

（1）各方案（n个）定性排序，遵循①＞0；②＜1；③＝0．5这3条规则。

（2）方案排序后，求各方案相对隶属度。

由同样优越0．5至无可比拟1之间，根据语气算子与标度的关系，计算各方案相对隶属度。

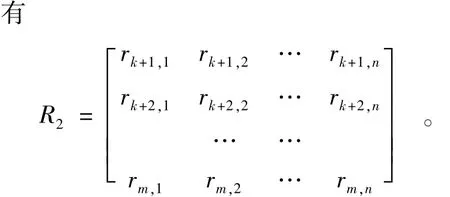
生态环境定性目标是越小越好，故都用式（5）计算。

2．3．3 求各目标的权重

（1）目标按重要次序定性排队。

（2）查语气算子与标度的关系［3］，计算各目标的模糊标度值uij。

（3）按式（6）求出对应的相对隶属度。

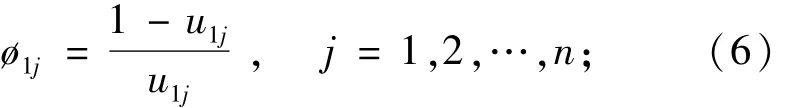
μ1j为排序第1位决策与第j位决策对比关于优越性的模糊标度值。

（4）将目标的相对隶属度进行归一化。

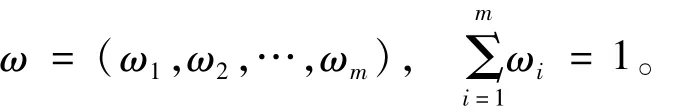
各目标重要性由大到小排序为：分洪效果、经济损失、蓄洪量、生态环境。各目标权重计算见表1。

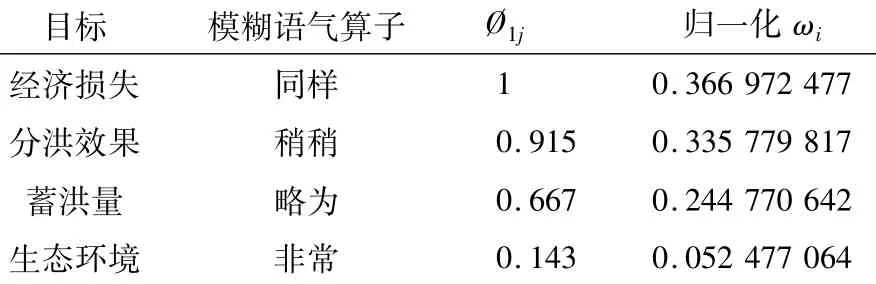
表1 各目标权重计算表Table 1 The calculation of every goal’sweight

2．3．4 求各方案相对隶属度

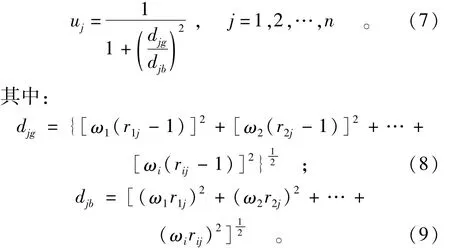
用式（8）和式（9）计算djg和djb，最后用公式（7）计算各方案uj。

2．3．5 求uj最大值

max uj，即最优方案为j方案。

3 模型在洞庭湖洪水调度方案选择上的应用

3．1 洞庭湖蓄滞洪区洪水调度模型

为了使洪水调度达到防汛部门调度的要求，选择合适的洪水调度模型显得尤为重要。对于荆江洞庭湖区这样大范围的区域，水系复杂，蓄滞洪区分散，运用一般的水文学模型或概化水动力学模型难以准确模拟其水流运动。在此情况下，河网水动力学模型成为现状情况下最适合的洪水调度方法。

一维河网不恒定流模型包括水流连续方程和动量守恒方程，采用隐式差分格式中的Preissmann四点偏心差分格式将方程进行离散线性化处理，结合河网汊点水流连续方程、河网动量守恒条件即构成封闭的河网方程组，一般采用三级解法求解，将河网方程组转化成只含有水位增量的汊点方程组。它的阶数与河网中的汊点数相同，但若汊点很多时，汊点方程组的系数矩阵也很大，给求解带来了困难。针对这个问题，文献［7］提出了汊点分组解法，基本思路是利用矩阵压缩，根据河网的实际情况和计算的需要，将河网中的汊点分为多组，能够有效地降低系数矩阵的阶数、节省存储量，从而大大提高计算的速度和精度。

文献［8］中把蓄滞洪区作为河网中可蓄水的汊点，通过堰流河段与其他河段相连接。将蓄滞洪区及相应的分洪口门纳入河网系统，形成蓄滞洪区洪水调度模型，也用汊点分组方法求解。

洪水调度时，由于分洪后，对下边界控制点的水位、流量产生一定的影响。同时，下边界控制点的水位（或流量）往往也是需要确定的要素，因而无法事先作为已知条件给定。所以，仅用水动力学方法解决下边界的问题有一定的难度，必须借助水文学的方法提供下边界条件。本文采用比较成熟的长江水利委员会的大湖演算模型［8］，把水文学方法与水力学方法相结合求得下边界条件。

3．2 洪水调度方案拟定

洞庭湖湖区由288个堤垸构成纵横交错的复杂河网。根据洞庭湖区近期防洪蓄洪工程规划，将288个堤垸分为重点垸、蓄洪堤垸和一般堤垸3类。其中，重点垸11个，总面积约6 698 km2，人口455万，是必须确保的堤垸；蓄洪垸23个，蓄洪总面积为2 870．03 km2，人口约167万，总有效蓄洪容积为161．91亿m3，其能防御一般性洪水，遇较大洪水时按计划扒口分蓄超额洪水，其余为一般堤垸。

对洞庭湖23个蓄洪垸的分洪调度原则如下：

（1）如果城陵矶水位没有达到控制水位34．40 m，而分蓄洪堤垸达到其控制水位，那么在水位超过控制水位0．5 m时，堤垸分洪。

（2）如果城陵矶水位达到控制水位34．40 m，而分蓄洪堤垸没有达到控制水位，那么由东向南，再向西将堤垸分成3组依次分洪，直至控制城陵矶水位34．40 m。分组情况如下：

第一组：江南陆城、君山建设建新、钱粮湖、大通湖四垸，总面积1 081 km2，总有效容积55．5亿m3。

第二组：屈原农场、共华垸、双华垸、茶盘洲农场、北湖、城西、义合、民主总面积857．1 km2，总有效容积53．1亿m3。

第三组：南汉、和康、安化垸、安昌、安醴、西官垸、九垸、围湖堤、集成安合、六角山总有效面积885．1 km2，总有效容积55．2亿m3。

（3）如果城陵矶、分蓄洪堤垸均达到控制水位，那么按先期达到控制水位的堤垸分洪。

（4）原则上，堤垸分洪口门位置设在临河或临湖的控制站上，假定每垸只设一个概化口门计算。

本文重点考虑1%频率的洪水情况，按照100 a一遇选取整体防洪设计洪水，运用蓄滞洪区调度模型，分析研究洞庭湖防洪工程体系的运用情况及防洪效果。具体设计方案为1996典型洪水组成1%设计标准。根据洪水调度原则中分组情况，拟订了6种开启方案：方案1为一组、二组、三组依次开启；方案2为二组、一组、三组依次开启；方案3为一组、三组、二组依次开启；方案4为二组、三组、一组依次开启；方案5为三组、一组、二组依次开启；方案6为三组、二组、一组依次开启。

表2 各方案评价目标归一化后的隶属度Table 2 Subordinateness degree of the program evaluation goals after normalization

3．3 洪水调度方案模糊优选

从蓄滞洪区蓄量、蓄滞洪区洪灾经济损失、蓄滞洪区分洪效果和生态环境4个目标来计算各方案的相对隶属度和目标权重，如表2所示。

按照模糊优选模型公式（7），得到1996年百年一遇的6种方案相对优属度向量为

u＝（0．998 711 44，1，0．999 056 47，0．999 944 991，0．997 965 58，0．999 751 59）。

从相对优属度向量可知，洪水调度方案2为最优。

洪水调度方案1，3，5开启蓄滞洪区情况：第一组中，江南陆城、君山建设建新、钱粮湖、大通湖四垸全部开启；第二组中，屈原农场、共华垸、双华垸、茶盘洲农场、北湖、城西、义合、民主全部开启；第三组中，南汉、和康、安化垸、安醴、西官垸、围湖堤、集成安合、六角山8个开启，九垸和安昌没有开启；还有洪湖分洪区。洪水调度方案2，4，6开启的蓄滞洪区比方案1，3，5少开了大通湖四垸。

定性分析如下：第一组靠近城陵矶，第二组靠近湘水和资水，第三组靠近三口。原始方案开启顺序是：第一组、第二组、第三组，当城陵矶水位达到控制水位，而分蓄洪垸还没有达到控制水位，就按顺序开启，然而优化方案开启顺序是第二组、第一组、第三组，1996年四水来水比较大，靠近四水的第二组先开启，承蓄了大部分四水的洪水，错开了四水和长江干流的洪峰，可以在少开大通湖四垸的情况下安全使洪峰通过。比较计算结果发现，优化方案四水附近每个蓄滞洪区蓄洪量和洪湖分洪量都比原始方案大，所有多的蓄洪量可以抵得上原始方案开启大通湖四垸的效果，所以不需要启用大通湖四垸就可以。在减少开启蓄滞洪区数目的同时，还使损失减少，所以，可以认为方案2为最优。

4 结 论

利用模糊优化理论建立了蓄滞洪区洪水调度方案模糊优选模型，能方便地将人的知识经验、意向纳入模型，同时可以考虑多目标中各目标的重要程度以及能将定性目标转化为定量目标，使方案选择更趋合理。

通过洞庭湖实例分析可以看出模糊优选模型在处理洞庭湖洪水调度方案选择问题时，较好地解决了洪水调度中影响因素众多，且有不确定性因素不易进行定量计算的问题，可为实际洪水调度方案选择提供参考。

［1］ 洪庆余．长江卷中国江河防洪丛书［M］．北京：中国水利水电出版社，1998．（HONG Qingyu．Vol Yangtze RiverChinese River Flood Control Series［M］．Beijing：China Water Conservancy and Hydropower Publishing House，1998．（in Chinese））

［2］ 倪晋仁，王光谦，李义天．洪湖分蓄洪区启用的若干问题研究［J］．自然灾害学报，1999，8（3）：14－21．（NI Jinren，WANG Guangqian，LIYitian．Some problems related to the utilization of Honghu flood divertion and storage works［J］．Journal of Natural Disasters，1999，8（3）：14－21．（in Chinese））．

［3］ 何 琦．浅析蒙洼蓄洪区运用时机［J］．治淮，2003，（12）：8－9．（HE Qi．Analysis of the time of the use of Mengwa detention basin［J］．Flood Control and Drought Relief，2003，（12）：8－9．（in Chinese））．

［4］ 要 威．行蓄洪区开启优化的研究［D］．武汉：武汉大学，2004．（YAOWei．Research on optimizing decision of using flood diversion works［D］．Wuhan：Wuhan University，2004．（in Chinese））

［5］ 陈守煜．多目标决策系统模糊优选理论、模型与方法［J］．华北水利水电学院学报，2001，（3）：136－140．

（CHEN Shouyu．A fuzzy optimum theory，model and approach formultiobjective decision making systems［J］．Journal of North China Institute ofWater Conservancy and Hydroelectric Power，2001，（3）：136－140．（in Chinese））

［6］ 陈守煜．模糊水文学与水资源系统模糊优化原理［M］．大连：大连理工大学出版社，1990．（CHEN Shouyu．Fuzzy Optimization Theory of Fuzzy Hydrology and Water Resources System［M］．Dalian：Dalian University of Technology Press，1990．（in Chinese））．［7］ 李义天．河网非恒定流隐式方程组的汊点分组解法［J］．水利学报，1997，（3）：49－57．（LI Yitian．A junctions group method for unsteady flow in multiply connected networks［J］．Journal of Hydraulic Engineering，1997，（3）：49－57．（in Chinese））

［8］ 李义天．洞庭湖分蓄洪区调度运用数学模型研究报告［R］．武汉：武汉水利电力大学，1997．（LI Yitian． The study report of flood controlmodel about storage and detention basin in Dongting Lake［R］．Wuhan：Wuhan Water＆Electric Power University，1997．（in Chinese））．

（编辑：曾小汉）

Optim ization of Flood Control of Storage and Detention Basin

LIU Yun1，LIYitian2，TAN Guangming2，DENG Jinyun2，SUN Zhaohua2，KOU Jisheng3
（1．Petroleum Engineering College of Yangtze University，Jingzhou 434023，China；2．State Key Laboratory ofwater Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China；3．Department ofmathematics，Shanghai University，Shanghai 200444，China）

On the basis of the characteristics ofmany factorswith uncertainties in flood control，multiobjective fuzzy optimal theory and method are introduced，and amultiobjective fuzzy optimal selectionmodel simulating flood control projects of storage and detention basin has been established，and the model has been applied in actual flood control，the problem ofmultiobjective decision system affected by certain factors and uncertain elements is successfully solved．

storage and detention basin；flood control；fuzzy optimization

TV122

A

1001－5485（2010）07－0022－04

20090818；

20100119

刘 云（1980－），男，江苏建湖人，讲师，博士，主要从事洪水调度和油气田开发的研究，（电话）13986660520（电子信箱）jh＿liuyun＠163．com。