非自治无时滞Lotka-Volterra竞争系统的有界性和持久性
秦丽华 樊小琳 刘 艳(.昌吉学院初教院 新疆 昌吉 800;
2.新疆工业高等专科学校 新疆 乌鲁木齐 830091; 3.新疆建设职业技术学院 新疆 乌鲁木齐 830054)
非自治无时滞Lotka-Volterra竞争系统的有界性和持久性
秦丽华1樊小琳2刘 艳3(1.昌吉学院初教院 新疆 昌吉 831100;
2.新疆工业高等专科学校 新疆 乌鲁木齐 830091; 3.新疆建设职业技术学院 新疆 乌鲁木齐 830054)
本文利用均值条件研究了N种群非自治无时滞的Lotka-Volterra竞争系统的有界性和持久性.并给出了一个数值例子来验证得到的结果。
Lotka-Volterra竞争系统;均值条件;持久性;有界性
一、引言
在研究生态学中,人们最关注的是生物种群的有界性、持久性、灭绝性和全局渐近稳定性。研究生态系统中种群有界、持久,种群灭绝的问题具有生物学意义和现实重要性。众所周知,Lotka-Volterra模型在生物数学中具有十分重要的理论和现实意义,由此成为该领域的重要课题之一。最近二十年来,国内外发表了大量关于Lotka-Volterra系统的文章,而这方面的专著也陆续出现,并且得到了很多重要的、有意义的结论。
文献[1-2]中的工作都是针对自治系统而言的,但是现实世界中种群的增长率总是随着时间不断变化的,即种群增长率ak不是常数,而是时间t的函数ak(t)。鉴于此,许多研究者针对具有时变增长率的Lotka-Volterra竞争系统,讨论了种群的持久性、灭绝性和全局渐近稳定性,得到了许多较好的结论,见文献[3-4]。
在文献[4]中,作者ShairAhmad和Alan C.Lazer研究了如下n种群Lotka-Volterra竞争系统
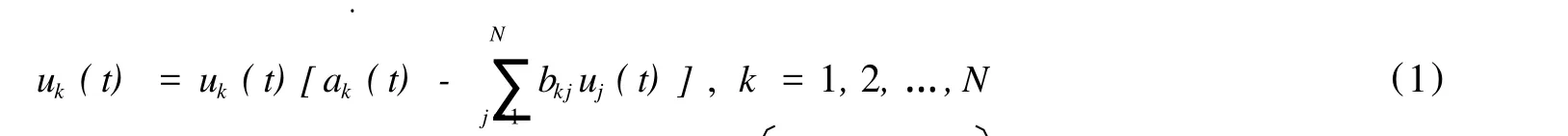
这里N≥2,种群增长率ak(t)是定义在的有界函数并且具有严格正的上下界,常数竞争率bkj非负并且bk>0对任意的k=1,2,…,N.
在研究生态模型过程中,认为生物种群之间的竞争率是常数也是不合理的,我们应该考虑种群间的时变竞争因素和种群自身的时变密度制约因素。从数学角度讲,考虑了时变关系的生态系统就是所谓的非自治生态系统。目前,关于非自治Lotka-Volterra竞争系统的研究工作很多,主要集中于讨论种群的持久性,灭绝性和全局渐近稳定性(见文献[5-6])。但是关于利用均值条件来讨论种群的有界性和持久性的研究结果并不多见。本文利用均值条件讨论更一般的非自治无时滞Lotka-Volterra竞争系统的有界性和持久性。
本文的主要结构如下,第一节引言中较全面的综述了Lotka-Volterra竞争系统在均值条件下种群持久、种群灭绝和全局渐近稳定性;第二节介绍了本文要用到的定义、假设及引理;第三节利用均值条件研究了N种群非自治无时滞的Lotka-Volterra竞争系统的有界性和持久性;第四节给出了一个数值例子来验证得到的结果。
二、模型描述、基本假设和定义
考虑如下n种群非自治Lotka-Volterra竞争系统:
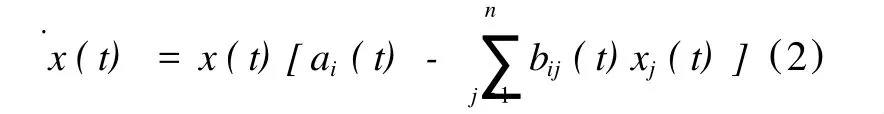
其中i∈N={1,2,…n},xi(t)表示第i种群在时刻t的密度,ai(t)表示第i种群在时刻t的内禀增长率,bij(t)表示第i种群和第j种群之间的竞争系数。
为了研究方便引入如下记号:
对于定义在[0,+∞)上的函数f(t),记:

显然此系统存在唯一解x(t)=(x1(t)…,xn(t)),易证明解是正的,即xi(t)>0,i∈N
定义2.1:设(x1,x2,…xn)是系统(1)的满足初始条件为xi(0)=Φi>0(k=1,2,…n)的解,称系统(1)是持久的,如果存在正常数m和M使得
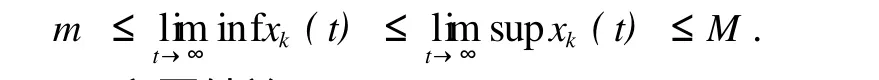
三、主要结论
定理1:在假设(H1)下,系统(1)以(4)为初始条件的解x(t)=(x1(t),x2(t),…,xn(t))满足如下不等式
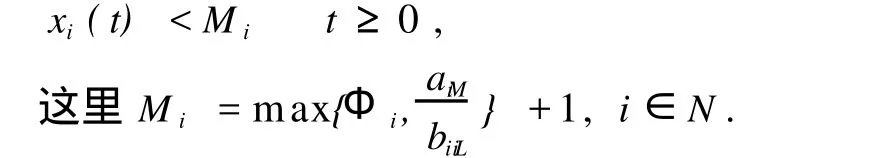
用反证法比较容易证明定理1的结论,这里省略证明。
定理2:在假设(H1)下,系统(1)以(4)为初始条件的解x(t)=(x1(t),x2(t),…xn(t))满足
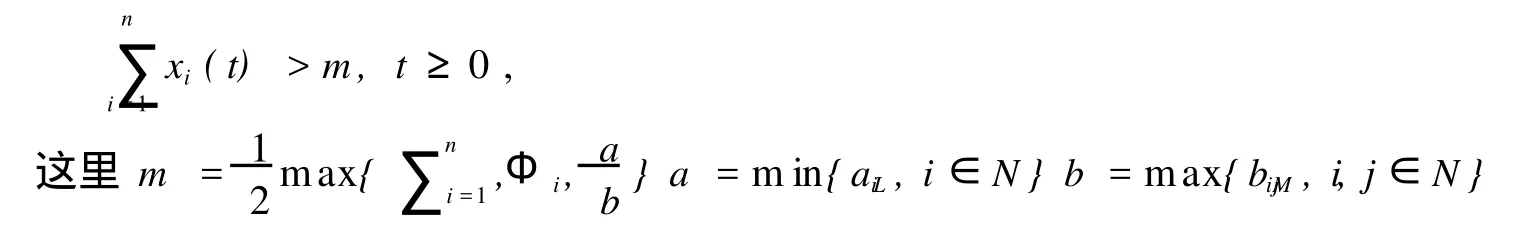
用反证法比较容易证明定理2的结论,这里省略证明。
定理3:在假设(H1)和(H2)下,系统(1)以(4)为初始条件的解
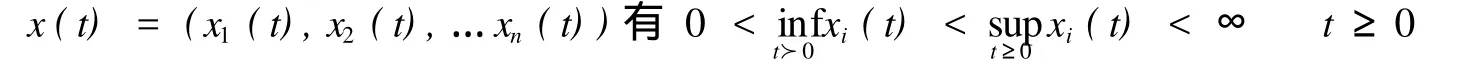
这个定理的证明需证明如下命题:
命题1:若定理3的结论不成立,那么存在系统系统(1)的以(4)为初值的解u(t)=(u1(t),u2(t),…un(t))以及存在集合N的最大非空真子集J满足

命题3:假设定理3的结论不成立,记L=NJ,那么存在常数ε>0使得对任意的k≥1和l∈L,有
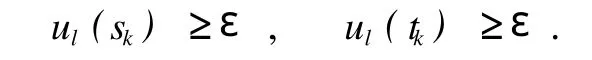
命题4:假设定理3的结论不成立,那么对任意的l∈L必存在常数xl使得
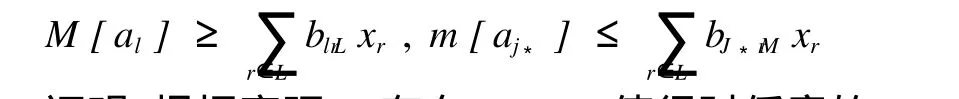
证明:根据定理1,存在M>0使得对任意的t≥0和l∈L有

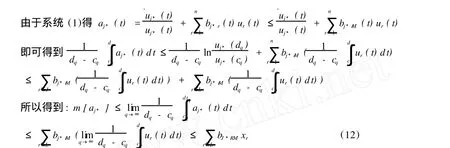
命题4:证明完毕。
下面用反证法证明定理3,假设定理3的结论不成立,那么根据命题1-4 知, 存在集合N的子集L,正整数1≤j*≤n且j*∉L,非负常数xl和yl(l∈L)使得(11)和(12)成立。
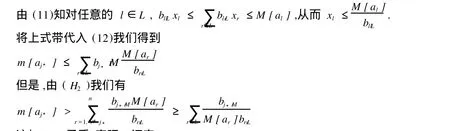
这与(12)矛盾,定理3证完。
由定理3,我们容易得到如下结论:
推论1:在假设(H1)和(H2)下,系统(1)持久。
四、数值实例和仿真
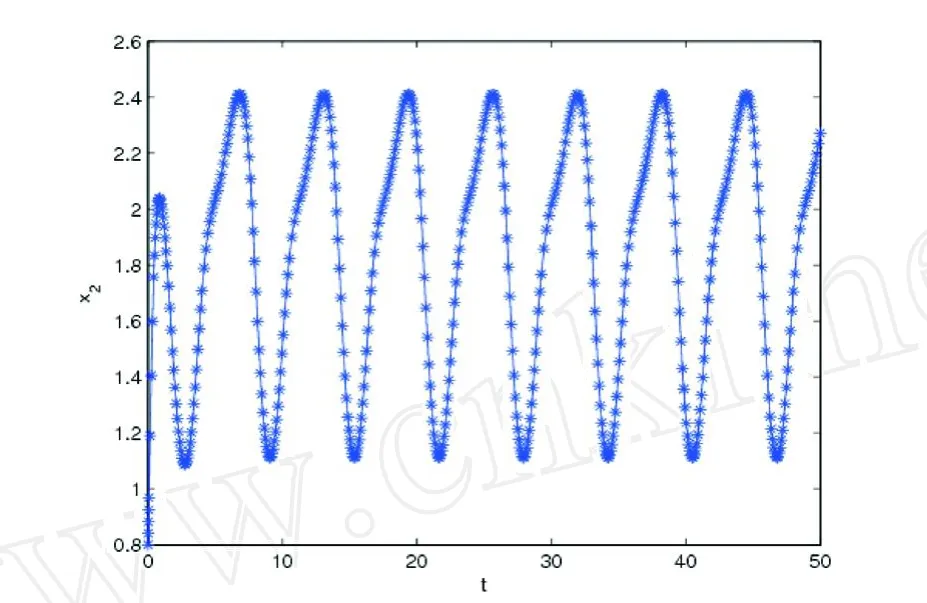
在本小节中,我们给出一个实例来说明本节结论的正确性和方法的有效性。
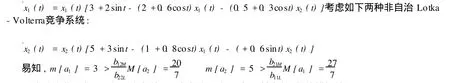
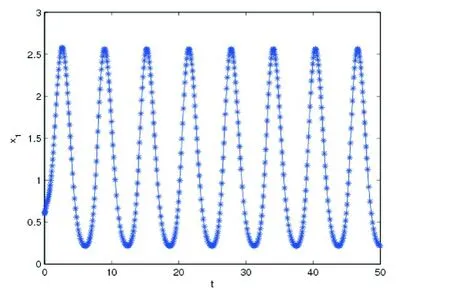
上述系统满足定理3的所有条件,所以种群x1和x2都是持久的,数值模拟结果见下图
[1]M.Braun,Differential Equations and theirApplications,Springer-Verlag,New York,1983.
[2]P.A.Keddy,Competition,Chapman&Hall,London,1989.
[3]S.Ahmand,A.C.Lazer,Average growth and extinction in a competitive Lotka–Volterra system,NonlinearAnal., 62(2005)547-557.
[4]S.Ahmad,A.C.Lazer,Necessary and sufficent average growth in a Lotka-Volterra system,Nonlinear Anal.,34 (1998)191-228.
[5]F.MontesDe Oca,M.L.Zeeman,Balancing survival and extinction in a nonautonomous competitive Lotka-Volterra Systems,Math.Anal.Appl.192(1995)360-370.
[6]滕志东.非自治Lotka-Volterra竞争系统的一些新结果[J].生物数学学报.1999,(14):385-393.
(责任编辑:马海燕)
O157.5
A
1671-6469(2010)05-0102-05
2010-07-25
秦丽华(1966-),女,陕西西安人,讲师,研究方向:应用数学、常微分方程理论及其应用。

