由伏雷内公式得到的结论
朱俊杰
(昌吉学院数学系 新疆 昌吉 831100)
由伏雷内公式得到的结论
朱俊杰
(昌吉学院数学系 新疆 昌吉 831100)
本文用伏雷内公式解决问题的理论方法给出了两个定理,并给出了严格的证明。
伏雷内公式;曲率;挠率
1 基本概念
曲线的基本公式——伏雷内(Frenet)公式是研究曲线几何性质的重要工具,它最早是由伏雷内在1847年发现的。而目前国内外的研究主要是采用活动标架法研究复流形到Gras sman流形的多重调和映照的性质,建立了广义伏雷内公式,应用它研究多重调和映照的若干性质。
自然参数[1]:设已给出曲线,如果我们以σ(t)表示从的弧长,即
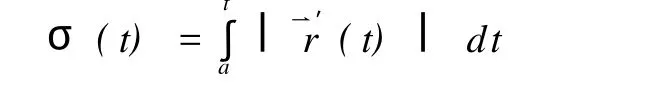

我们把s称为曲线的自然参数。
在附着于曲线上每一个非逗留点P,我们确定了三个向量,即切向量,主法向量,副法向量γ⇀,它们都是互相垂直的单位向量而且按这个次序构成右旋系,因此,他们之间有如下关系:

定义[2]空间曲线(C)在P点的曲率为
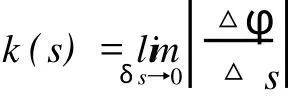
其中△s为P点及其临近点P1间的弧长,△φ为曲线在点P和P1的切向量的夹角。

挠率的绝对值是曲线的副法向量(或密切平面)对于弧长的旋转速度。
引理[4](伏雷内公式)若分别表示曲线的切向量,主法向量和副法向量,k,τ分别表示该曲线的曲率和挠率,则

2 主要结果


[1]梅向明,黄敬之.微分几何[M].高等教育出版社,2003.
[2]梅向明,王汇淳.微分几何学习指导与习题选解[M].高等教育出版社,2003.
[3]吴大任.微分几何讲义[M].高等教育出版社,1957.
[4]陈省身,陈维恒.微分几何讲义[M].北京大学出版社,1983.
(责任编辑:马海燕)
O186
A
1671-6469(2010)05-0107-02
2010-06-02
昌吉学院科研基金资助项目(2010SSQD022)
朱俊杰(1982-),男,新疆阿克苏人,昌吉学院数学系,助教,研究方向:微分几何。

