《物理化学》教学研讨——热力学基本方程记忆法

陈世平，朱必学

（贵州大学化学系，贵州贵阳550025）

《物理化学》教学研讨
——热力学基本方程记忆法

陈世平，朱必学

（贵州大学化学系，贵州贵阳550025）

热力学基本方程在热力学中具有十分重要的地位，一些文献资料曾对这几个公式的记忆方法作过研讨。作者根据多年的教学经验，也总结了一套关于这几个公式的记忆方法。

热力学；基本方程；记忆法

单组分均相系统的四个热力学基本方程，在热力学中具有极其重要的地位，因此，对化学专业物理化学课程和物理专业热力学课程的学习者来讲，应该做到牢固掌握，强力记忆，准确书写，灵活运用。但这四个公式涉及的量虽然并不多，而外观形式上却十分相似，因而常导致记忆混淆而出现错误。为此，一些从事基础理论教学的教师，为找到一个关于这四个方程的简便记忆方法而做了很多工作。比如，林朝金的图形法[1]，陈家玮的一句话巧记法[2],宋刘斌的图形、坐标兼用法[3]以及吴新明的特性函数法[4]等。这些方法都很好，而且各有特色。

笔者在多年的物理化学教学实践中也总结了一套关于这四个方程的记忆方法，其特点是：记忆方法本身无需记忆且简单可靠；使用时，任何一式都可信手写来，没有再思维的过程。此方法已在教学中试用多年，试用效果良好。

1 热力学四个基本方程记忆法

基本方程涉及到的系统性质，一共是8个，即p、V、T、U、H、S、A和G。这八个函数，按是否具有能量的量纲，可分为两组：其中，U、H、A、G具有能量的量纲，p、V、T、S不具有能量的量纲。但在不具有能量量纲的这一组中，p与V相乘，T与S相乘后也都具有了能量的单位。从形式上看，四个基本方程就是用p与V以及T与S的某种“组合”来分别表达另外四个状态函数的微分量。这样，在方程中，p与V不能分开，T与S也不能分开。

首先，T与S的组合有两种：

TdS，因δQr=TdS，故代表热量（严格地讲，只有在可逆过程中，TdS才代表热），因在热力学第一定律中为正，故在基本方程中取正号；

SdT，是T与S组合中的非热量形式，在基本方程中取负号。

即，热取正而非热取负。

同理，p与V的组合也有两种：

pdV，体积功（也只有在可逆过程中，pdV才代表体积功），因在热力学第一定律中取负号，故在基本方程中也取负号；

Vdp、是p与V组合中的非体积功形式，在基本方程中取正号。

即，功取负而非功取正。

基本方程的书写以U、H、A和G四个函数在过程中的某个具有特征性的表现为口诀。在口诀中：把“热”视为“TdS”；把“等”字看作是微分符号“d”（如等温则为dT）。

热力学四个基本方程是

式（1）因dU=δQv，故说为“内能差（dU）是等容（dV）下的热（TdS）”：由于dV前只能是p，pdV为功取负号；TdS为热取正号。因此，基本方程第一式为

式（2）因dH=Qp、故说为“焓变（dH）是等压（dp）下的热（TdS）”：由于dp前只能是V，而Vdp为非功取正号；TdS为热取正号。因此，基本方程第二式为

式（3）等温等容是亥姆霍兹自由能的变化值作为过程方向判据的应用条件，因此说“亥姆霍兹自由能（dA）是等温（dT）等容（dV）位”：dT前只能是S，SdT非热取负号；dV前应是p，pdV是功取负号。因此，基本方程第三式为

式（4）等温等压是吉布斯自由能的变化值作为过程方向判据的应用条件下，因此说“吉布斯自由能（dG）是等温（dT）等压（dp）位”：dT前只能是S，SdT非热取负号；dp前应是V，Vdp是非功取正号。因此，基本方程第四式为

2 准确记忆热力学基本方程的重要意义

2.1 记忆八个对比关系式[4]

根据四个热力学基本方程，能随时将八个对比关系式准确无误地写出来。

比如，依式（1） dU＝TdS-pdV

在等容条件下，dV＝0，将dS移到左边为分母并以V作为右下标（等容），则得

同理，仍依式（1），在等熵条件下，可得

按照与获得式（5）和式（6）完全相同的方法，分别以式（2）、式（3）和式（4）为参照，就可分别得到其余六个对比关系式：

依式（2）dH＝TdS+Vdp，得

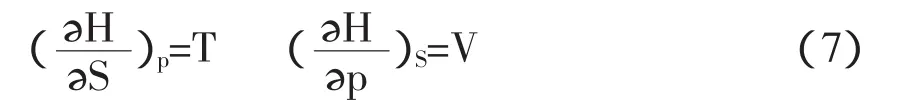
依式（3）dA＝-SdT-pdV，得

依式（4）dG＝-SdT+Vdp，得

2.2 写出麦克斯韦关系式[5]

在准确地记忆了四个热力学基本方程的基础上，可轻易地书写出麦克斯韦关系式，而麦克斯韦关系式是在热力学函数关系式的证明中常用的偏微分替换式。比如，

由式（1）可得 （∂T/∂V）S＝-（∂p/∂S）V

相应地，由式（2）、式（3）和式（4），依次可得

麦克斯韦关系式有这样的特征：

（1）作为下标的量，总是与作为分子的量相乘后形成能量单位的那个量（如分子为T，则下标一定是S；而分子为V时，下标一定是p）；

（2）在热力学基本方程中，等式右边两项为一正一负时，则，由该式产生出来的相应的麦克斯韦关系式，带负号。

2.3 确定特性函数的特征变量

当U、H、A、G和S分别作为特性函数时，在准确地记忆了四个热力学基本方程的基础上，可以立即确定每个函数所对应的特征变量，因为每个公式中的微分量就是所表达的函数的特征变量。比如，

由式（1） dU＝TdS-pdV

可知，热力学能U的特征变量是熵S和体积V；

相应地：焓H的特征变量是熵S和压力p；亥姆霍兹自由能A的特征变量是温度T和体积V；吉布斯自由能G的特征变量是温度T和压力p。

当把式（1）写为dS＝（1/T）dU＋(p/T)dV时，可得S的第一组特征变量，S-U、V；

当把式（2）写为dS＝（1/T）dH-(V/T)dp时，可得S的另一组特征变量，S-H、p。

2.4 准确地辨识用不同状态函数所表示的化学势

由于用不同状态函数所表示的化学势的脚标，就是相应状态函数作为特性函数时所对应的特征变量。因此，准确地掌握四个基本公式，也就可准确地辨识并随意写出用任一状态函数来表达的化学势，而不致于与偏摩尔量相混淆。

2.5 准确地掌握用不同状态函数所表示的广义的表面吉布斯自由能[6]

与化学势的表达相似的还有广义的表面吉布斯自由能γ，用U、H、A、G来表达广义的表面吉布斯自由能γ时，脚标也都是它们作为特性函数时所对应的特征变量。

3 小结

在物理化学教学中，把重要公式的记忆法列为教学内容，是教学方法改革的一种尝试。在记忆方法的讲述中，可加深学生对公式的理解和认识，从而增强学习积极性，提高学习效果。

本文介绍的四个热力学基本方程的记忆方法，所涉及的各记忆要素，均源于物理化学教学过程。因此，只要在教学过程中适时适当地加以强调，则在了解本记忆方法后，学生们便可准确无误地记住这四个热力学基本方程。又由于四个热力学基本方程与八个对比关系式、与四个麦克斯韦关系式有着本末般的关系，因此，八个对比关系式和四个麦克斯韦关系式也随之有了有效的记忆方法。

[1]林朝金.热力学函数关系式、全微分关系式和麦克斯韦关系式的简捷记忆[J].四川师范大学学报,1995,(6):96-97.

[2]陈家玮.杨忠芳.张德会.由“一句话”巧记热力学函数关系式[J].中国地质教育,2005,(4):110-112.

[3]宋刘斌.彭三军.关于物理化学教学中公式记忆法的探讨[J].科教文汇,2007,(8):90.

[4]吴新明.焦雅文.物理化学中十九个基本热力学函数关系式的记忆方法[J].湖北教育学院学报,2001,(5):29-30.

[5]傅献彩.物理化学（第五版,上册）[M].北京：高等教育出版社,2005.170.

[6]傅献彩.物理化学（第五版,下册）[M].北京：高等教育出版社,2006.315.

（责任编辑：朱 彬）

A Discussion on the Teaching of"Physical Chemistry"——A Memory Method of Basic Equations of Thermodynamics

CHEN Shi-ping，ZHU Bi-xue
（Department of Chemistry，Guizhou University，Guiyang550025，China）

The basic equation of thermodynamics is very important in the study of thermodynamics.The memory method of these equations has been discussed in some literatures.However,the author has also summed up a set of memory methods based on years of teaching experiences.These methods will be ushered to the readers in this paper.

thermodynamics；basic equation；memory method

G424.1

C

1009-3583（2010）-02-0089-03

2009-11-15

陈世平，男，贵州惠水人，贵州大学化学系副教授。