一种六杆并联机床数控系统程序设计

马明明,王友林,李 娟

(山东理工大学机械工程学院,山东 淄博 255049)

并联机床以其不可替代的结构简单、刚性好、运动定位精度高、运动质量小等优势已成为机床家族最具发展潜力的一员[1],被称为“21世纪的机床”,是当前各国的重点技术发展项目[2].但测量控制的计算量大、操作空间小、价格高的缺点严重制约了并联机床的工业应用,使其目前仍停留在实验室研发阶段,还不能改变当前串联式数控机床的主体地位.针对并联机床控制计算量大的缺点,本文研究一种算法较为简单的、具有3大模块的并联机床应用程序.

1 程序开发环境

本系统程序所控制的机床为6-UPS并联运动机床[3],通过控制6杆的杆长变化达到控制刀具位姿的目的.系统程序在Microsoft VC++6.0软件开发环境下开发,选择多文档(Multiple document)应用程序,每个文档对应一个数据处理模块.应用文档/视图结构可以使数控系统的窗口界面具有Window s窗口操作风格,操作者使用起来容易上手.

2 机床结构参数设置(模块1)

2.1 机床驱动系统

机床驱动系统由运动控制卡、步进电机驱动器、步进电机和丝杠螺母机构组成.本系统运动控制卡选用研华PCI-1750,步进电机驱动器选用DL-025,步进电机选用57BYGH603.这里仅给出1条杆的驱动系统接线图[4](如图1所示),其余5条杆类似.

图1 驱动系统接线图

2.2 机床主要结构参数及对刀

设机床的坐标系(笛卡尔坐标系)原点在6个静铰中心形成的正六边形的几何中心上,静平台、动平台各铰链中心的相对位置分别如图2、图3所示.初始时,动、静平台水平放置且其铅垂方向(Z轴方向)距离为515 mm,刀头点至动铰中心的距离为227 mm.

对刀是指使刀头点相对于机床坐标系有正确的初始位姿,即动静平台水平放置且刀头点沿铅垂方向(Z轴方向)与静平台铰链中心距离为742 mm,各杆长度相等,经计算长度L为

图2 静平台铰链分布图

图3 动平台铰链分布图

对刀模块中的调整运行组框能响应鼠标点击从而调节各杆长度,倍距选择组框能选择各杆调整运行时伸长或缩短的距离.这样对刀模块就实现了用计算机软件代替手摇脉冲发生器的功能.相应的数控系统界面如图4所示

图4 机床结构参数设置与对刀操作界面

3 NC代码编写及其相应的数据处理(模块2)

3.1 NC代码编写格式与翻译

参照当前普通数控机床的代码编写规则,本系统的基本插补代码编写规则如下:

其中:N为代码的行号;G为空间直线插补命令,G00为快速进给,G01为低速直线进给,G02为空间顺时针圆弧插补,G03为逆时针圆弧插补(由Z轴负方向看去);X,Y,Z为刀头点在机床坐标系中的位置;A,B,C为刀具轴线分别与X,Y,Z轴的夹角;I,J,K空间圆弧圆心坐标.X,Y,Z,A,B,C确定了刀具在机床坐标系中的位姿.

每行NC代码中X,Y,Z,A,B,C既是上一行代码所代表刀具位姿的终点,又是下一行NC代码所代表刀具位姿的起点.

NC代码的翻译是将NC代码按一定的格式提取出来,为计算机的插补运算做好准备.例如:NC代码行为N025 G01X0.Y-7.20 Z-742.A2.30 B5.6 C0.,则翻译后写入文件的格式为(25,0,-7.20,-742,2.30,5.6,0),这样NC代码中有用的信息就能提取出来并保存在文件中.

3.2 空间直线插补

并联机床的机床坐标系是虚拟的,并没有实际的运动轴与其对应,因而并联机床又称为虚拟轴机床,这样特殊的机械结构使得并联机床有完全不同于普通数控机床的插补算法.

本系统采用小球面分割法,插补算法如下:

①将刀具的运行轨迹看成是一条曲线,将小球面球心放置在曲线的起点上,这样曲线和小球面必有一个交点,记录下此交点

②将小球面的球心放在上一步插补的焦点上,这样空间曲线便与小球面有两个交点,依据刀具加工方向对两个交点取舍,保留选取的交点

③依次进行,空间曲线就被小球面离散成一系列的点,这些点按一定的顺序被保存在了文件中.

空间中直线与圆的插补是最基本的插补线形,因为一来在插补其他空间曲线时,可以用直线与圆弧来拟合其他空间曲线;二来可仿照空间直线与圆弧的插补算法来衍生其他空间曲线的插补算法.

3.3 空间直线的插补算法

如图5所示,设某有向直线段由起点E(L,M,N)至终点F(P,Q,R),满足L≥P,M≤Q,N≤R且L=P,M=Q,N=R不同时成立,分割小球面球心(A,B,C)在该有向直线段上,其半径为r,于是有

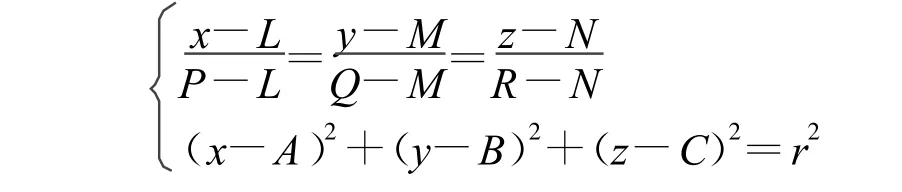
可求得小球面与有向直线段的两个交点,记为U(x1,y1,z1),V(x2,y2,z2),在程序中取舍交点的标准就是有向直线段的方向,两交点取舍算法如下:

①若x1＞x2,则选取点V;若x1＜x2,则选取点U;若x1=x2,则执行下一步;

②若y1＜y2,则选取点V;若y1＞y2,则选取点U;若y1=y2,则执行下一步;

③若z1＜z2,则选取点V;若z1＞z2,则选取点U;若z1=z2,则执行下一步;

④报错“注意检查NC代码是否重复!”

图5 空间直线分割示意图

3.4 空间圆弧插补算法

如图6所示,设空间某有向圆弧,起点E(L,M,N),终点F(P,Q,R),圆心(I,J,K).分割小球面球心(A,B,C)在该有向圆弧线段上,其半径为r.坐标系O-xyz的底矢分别为i,j,k于是有[5]:

解方程组(1)可以求得空间圆弧与小球面的两个交点,记为U(x1,y1,z1),V(x2,y2,z2),下面讨论圆弧与小球面两个交点的取舍问题.

先将空间圆弧分类,按空间圆弧是否垂直X轴,Y轴分3大类:(1)空间圆弧垂直于X轴;(2)空间圆弧垂直于Y轴;(3)空间圆弧既非垂直于x轴,又非垂直于y轴;

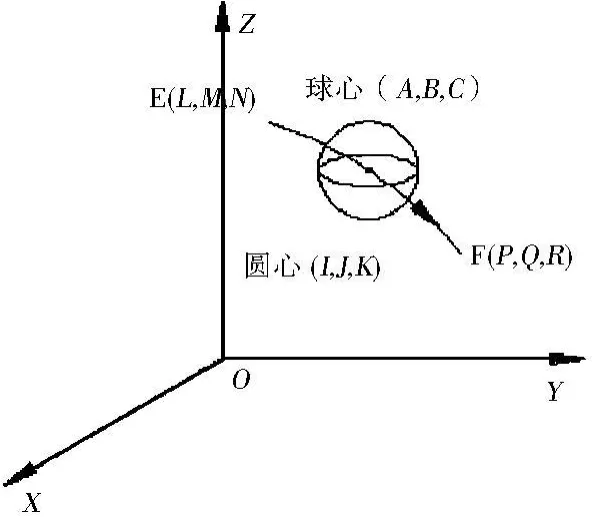
图6 空间圆弧分割示意图

现针对这3大类圆弧现分别做小球面分割:

1)垂直于X轴的空间圆弧插补算法.

①将空间圆弧圆心移至机床坐标系原点,记录偏移量.

②将X轴和Z轴互换(这样圆弧处于OXY坐标系中),根据要插补圆弧在OXY坐标系中象限与插补方向进行两交点的取舍,并保存选取的交点.例如图7所示的第一象限的逆时针圆弧,在点U,V中选取具有较小X坐标的点,其余的几种情况可采用类似的方法.

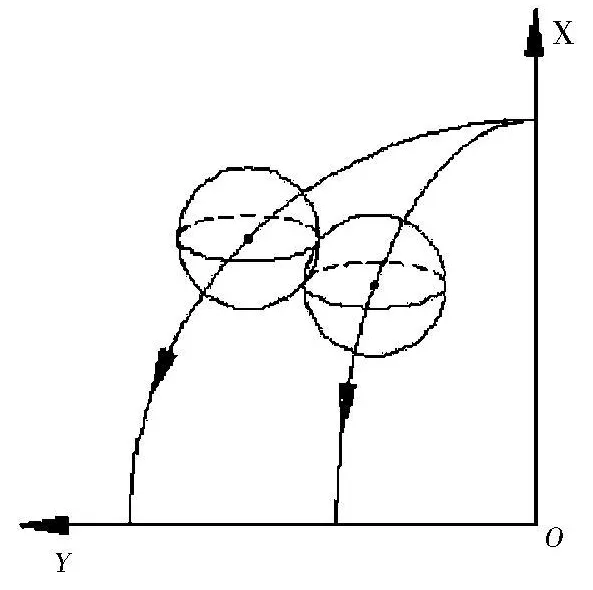
图7 第一象限逆时针圆(椭圆)弧

③将选取点的X,Z坐标互换.

④将选取点减去①步的偏移量,并保存.

2)垂直于Y轴的空间圆弧插补算法:完全类似于垂直于X轴的空间圆弧插补算法.

3)既非垂直于X轴,又非垂直于Y轴空间圆弧空间圆弧的插补算法

①将空间圆弧圆心移至机床坐标系原点,记录偏移量.

②根据要插补圆弧在OXY坐标系中投影的象限与插补方向进行两交点的取舍,并保存选取的交点.例如图7所示空间圆弧在OXY第一象限的椭圆弧投影,在点U,V中选取X坐标值较小的点,其余的几种情况可采用类似的方法.

③将选取点减去①步的偏移量,并保存.

截取的某圆弧的离散点如图8所示.

图8 保存某圆弧离散点的.txt文件

由于空间圆弧的插补算法决定了在编写加工空间圆弧的NC代码时,需要按照3大类空间圆弧的插补算法来写,因此,不能出现跨象限现象,否则将出现插补错误.

3.5 后处理

本系统的后处理是指将插补得到的刀具轨迹离散点最终转变为各步进电机的脉冲分布,其过程如下:

1)依据刀头点在轨迹离散点上的姿态,计算动平台铰链中心在机床坐标系中的坐标.

将机床坐标系O-XYZ平移至刀头点所在位置,(x,y,z)变为O′-X′Y′Z′,如图9所示,设刀具轴线(Z″轴)与X′、Y′、Z′轴的夹角分别为 α,β,γ.由于刀具可绕自身轴线旋转,因此仅给出x,y,z,α,β,γ6个参数并不能确定刀具的位姿和动平台坐标系O′-x″y″z″.本系统按照“伸缩杆变化最小原则”提供了一种算法,可依据这6个参数确定动平台的唯一位姿.刀具轴线所在轴O′Z″与O′Z′轴唯一确定一个平面(如图9中的阴影部分所示),过O′点做与平面垂直的直线(如图9中虚线所示),固连在动平台上的刀具轴线绕这条虚线转动γ角,这样动平台的位姿就可唯一确定.

图9 坐标转换示意图

设坐标系O′-X′Y′Z′的底矢为i,j,k,则转轴的方向为l,且

可求出坐标系O′-X′Y′Z′绕转轴转过γ角形成动平台坐标系O′-X″Y″Z″,最终可求出O′-X″Y″Z″各底矢与O′-X′Y′Z′各底矢的交角,结果见表1.

表1 O′-x″y″z″与O′-x′y′z′的相对姿态

以1杆动铰中心为例,计算刀头点在(x,y,z,α,β,γ)位姿下动铰中心在机床坐标系中的坐标(x1,y1,z1).由机床床身结构可知,1杆动铰中心在动平台坐标系中的坐标值为(105.0892,32.5,227),依据坐标轴的移动与旋转变换,由式[5]可求得(x1,y1,z1),同样可求得其他5个动铰中心在机床坐标系中的坐标.因此可求出各个分割点处(x,y,z)及刀具姿态(α,β,γ)对应的动铰中心机床坐标系坐标.

2)各杆长度计算

由床身结构可知,在机床坐标系中1杆静铰中心的坐标值为(363.7307,210,0),某时刻其动铰中心为(x1,y1,z1),据空间两点的直线距离公式,可得1杆的长度l1:

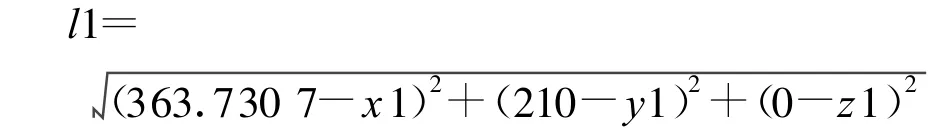
同样计算其他5杆长度,并将结果保存,各杆长度保存格式如图10所示,图10中最后一栏是插补速度代号.

图10 各杆长度保存格式

3)计算脉冲数

读取相邻两插补点对应的杆长值,易得各杆的杆长变化 Δl(mm).以1杆为例,第t步杆长为lt,第t+1步杆长为lt+1,则杆长变化为 Δl1=lt+1-lt.机床传动系统参数如下:步进电机步距角为0.9°,同步齿形带减速比为2,滚珠丝杠螺距为4 mm,则完成1杆在该步插补所需的脉冲数n1为

注意n1可能不是整数,程序中设一个变量将各步小数部分累加,若个位数变为+1,则保存n1+1,若为-1,则保存n1-1.同样,其他各杆所需脉冲数也可确定,并将其保存,保存格式如图11所示,图11中最后一栏是插补速度代号.

图11 插补脉冲数目保存格式

4)分配各杆每步脉冲

各杆每步脉冲分配要均匀,以尽量保证步进电机转动平稳.生成的脉冲分配文件(加工文件)如图12所示.举例说明,图中-4表示杆4电机将响应一个反向脉冲.插补与后处理程序界面如图13所示.

图12 加工文件格式

图13 插补与后处理程序界面

4 仿真与加工(模块3)

后处理完成之后,对生成的插补文件进行仿真.该仿真主要是在实际加工之前,通过提取生成的插补文件,在系统程序的界面上对插补的轨迹进行仿真.通过研华PCI-1750运动控制卡提供的函数,将加工文件转化为步进电机的转动,控制卡的操作与接线可详见说明书.仿真加工的界面如图14所示,该界面仿真了插补的轨迹,并跟踪插补过程中的每一个离散点,通过大量的实际加工和仿真证明了本系统算法的正确性.

图14 仿真/加工界面

[1]王润孝.先进制造技术导论[M].北京:科学出版社,2004.

[2]卜基桥.新型并联加工机床[J].现代制造,2007(13):12-13.

[3]张曙.并联运动机床[M].北京:机械工业出版社,2003:45-47.

[4]刘华,袁先垚,王友林.并联机床运动控制卡接口设计[J].山东理工大学学报(自然科学版),2008,22(1):49-51.

[5]黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.