基于双窗口小波-Contourlet变换的图像融合算法

高雪妮

（广西大学 计算机与电子信息学院，广西 南宁 530004）

基于双窗口小波-Contourlet变换的图像融合算法

高雪妮

（广西大学 计算机与电子信息学院，广西 南宁 530004）

提出一种基于双窗口小波-Contourlet变换的图像融合算法。首先采用小波-Contourlet变换对图像进行分解，接着采用两种不同尺寸的窗口计算系数的特征值：低频子带采用区域能量法和高频子带采用区域方差法，分别比较双窗口下的高频子带和低频子带的系数特征值，比较的结果作为得到融合系数选择的依据，最后采用逆小波-Contourlet变换得到融合图像。仿真实验证实，在特征类型选择一致的情况下，该方法的融合性能优于小波变换法和Contourlet变换法，融合图像质量较好。

小波变换；contourlet变换；图像融合；双窗口

1 引言

由于小波变换在高维的情况下并不能充分利用图像本身特有的几何特征，并不是最优的和“最稀疏”的函数表示方法，因此，人们致力于发展一种新的高维函数的最优表示方法。多尺度几何分析 (multistage geometric analysis,MGA)就是近年来发展起来的一类彼此及其相似的图像表示方法，它在数学分析、计算机视觉、模式识别、统计分析等不同学科中得到研究人员的关注。

2002年，Do M N和VetterliM提出了一种图像二维稀疏表示方法：Contourlet变换，[1-2]也称塔型方向滤波器组 (PDFB，Pyramidal Directional Filter Bank)，是多尺度几何分析方法中表现较为突出的一种方法。Contourlet变换的基函数的支撑区间具有随尺度变化的长条形结构，改变化将多尺度分析和多方向分析分开进行，满足“抛物线尺度关系”，满足“各向异性尺度关系”，因而能够运用较少的系数对奇异曲线进行线性逼近，是一种“真正”的二维图像稀疏表示方法，对于细小的有方向的轮廓和线段的表达有着独有的优势。它不仅继承了小波变换的多分辨率时频分析特征，而且拥有良好的各向异性特征，它能用比小波更少的系数来表示光滑的曲线，是一种多分辨率的、局域的、多方向的图像表示方法。

Contourlet变换采用拉普拉斯金字塔变换分解，由于拉普拉斯金字塔没有对高频子带进行下采样，因此比小波分解多出了1/4的高频子带数据冗余。为了降低冗余，Ramin Eslami和Hayder Radha于2004年提出了小波-Contourlet变换，[3]采用二维小波变换对图像进行分解而不是拉普拉斯金字塔变换。由于小波分解与重构都是无冗余的，因此，小波-Contourlet变换不会产生冗余。本文对基于小波-contourlet变换算法进行改进，采用双窗口策略对融合系数进行选择，改进的算法能有效捕捉图像各向异性的高频信息，克服了信息冗余，降低了融合系数选择的失误率。

2 小波-contourlet变换

2.1 contourlet变换

Contourlet变换是多尺度分析方法中最为突出和理想的一种，Contourlet变换由两个部分组成：拉普拉斯金字塔变换和方向滤波器组。其分解过程表示如下：首先采用拉普拉斯金字塔变换对输入图像进行多尺度分解，得到输入图像的高频子带和低频子带，其中，低频子带是输入图像经过二维低通滤波和下采样后得到的低频成为，其分辨率为输入图像的1/2，高频子带则是输入图像与同级尺度的低频子带上采样滤波后的差值，接着，对低频子带继续采用拉普拉斯金字塔变换进行分解，得到一系列不同分辨率上的高频子带和一个低频子带。然后，对不同分辨率上的各高频子带采用方向滤波器组进行分解，得到不同方向的带通方向子带。上页图1给出了Contourlet变换的分解原理图。上页图2是Contourlet变换的频域分解图。

图1 Contourlet变换原理图

图2 Contourlet频域分解图

图3 四方向滤波器组框图

2.2 小波-contourlet变换

在Contourlet变换中，由于拉普拉斯金字塔变换没有对高频子带进行分解，因此Contourlet变换比小波变换多出了1/4的高频子带数据冗余。为了降低数据冗余，Contourlet变换采用拉普拉斯金字塔变换分解，由于拉普拉斯金字塔没有对高频子带进行下采样，因此比小波分解多出了1/4的高频子带数据冗余。为了降低冗余，Ramin Eslami和Hayder Radha于2004年在文献 [6]中提出了小波-Contourlet变换，采用二维小波变换对图像进行分解而不是拉普拉斯金字塔变换。由于小波分解与重构都是无冗余的，因此，小波-Contourlet变换不会产生冗余。基于小波-Contourlet变换的基本思想是：利用小波变换的分解方式代替拉普拉斯金字塔分解，分解后得到一个低频子带和三个方向的高频子带：水平方向、垂直方向和对角线方向，[7]然后采用方向滤波器对小波分解中的低频子带进行多方向滤波。小波-Contourlet变换比小波变换、Contourlet变换更能稀疏地表示图像的几何结构特征。图4是图像方向数为 [4,2,2,0]的3级小波-Contourlet变换示意图。

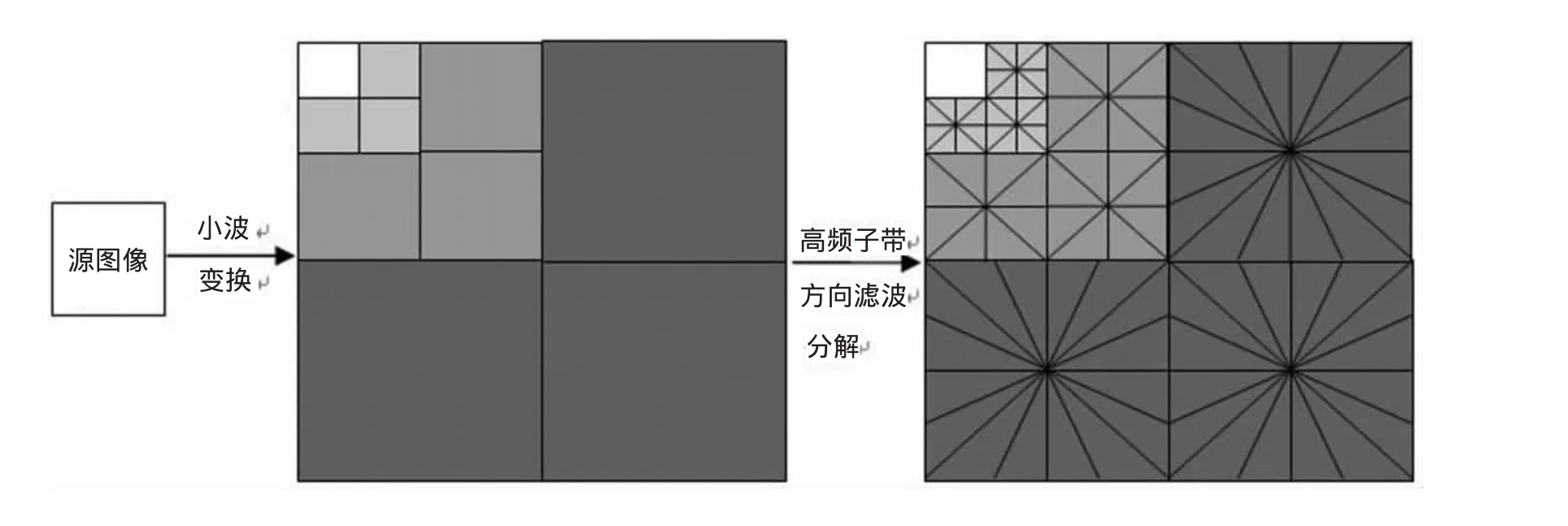
图4 小波-contourlet变换

3 融合规则

对图像进行小波变换，得到一个低频子图和3n个高频子图 （n为分解层数），小波-Contourlet变换是在小波变换的基础上，继续对3n个高频子图采用方向滤波器组进行方向滤波，滤波的方向数常用的有4,3,2,1,0。由于低频子图主要是图像的轮廓信息，可以采用局域能量的融合规则，而高频子带代表了图像的边缘、纹理、突变等细节信息，因此可以采用局域方差的融合规则。

以图像中某像素f(x,y)为中心的k×k窗口W的方差可以定义为：

以图像中某像素f(x,y)为中心的k×k窗口W的能量可以定义为：

窗口能量值越大，则表示该窗口内的信息越丰富。

目前，基于区域的Contourlet变换的融合算法中，都是基于单窗口的，如文献 [8]提出的算法中，低频系数根据区域能量进行选择，高频系数根据局域对比度进行选择；文献 [9]提出一种基于区域特征自适应的融合算法，高频分量以空间频率为度量标准结合自适应算子进行区域的自适应融合。区域特征值相对于单个系数值能更充分地反映子带的特征信息，但区域的大小对特征值的影响也是不能忽略的。小波-Contourlet变换将图像的高频子带分解到不同方向上，变换后的能量集中在有限的系数上，其余大部分系数的幅值接近于零。采用区域特征值作为判断指标，则必须考虑到区域的大小对特征值的影响情况，而目前采用的区域大小都是随机的，或者是通过多次实验选择一个最佳区域大小，这对实时系统的实现是相当不利的。本文采用双窗口的融合策略，通过不同窗口 （即区域）大小选择不同的融合系数，再根据两类方案融合系数的特点进行最终融合系数选择。

本文算法具体步骤如下：

步骤1 对源图像A和B采用小波变换进行分解，得到一个低频子带Li和一系列高频子带H，其中，i=A或B；j=HL或LH或HH，代表水平、垂直、对角线三个方向；k=1，2，…N，代表分解的层数。

步骤3 对低频子带Li，采用k1×k1窗口逐个系数进行扫描，计算窗口的能量Ei,h，其中h表示低频子带的第h个系数。

步骤5 比较EA,h和EB,h的大小，作为融合图像低频子带系数的选择依据：

其中，RLh代表融合图像低频子带系数。

步骤7 采用k2×k2（k1≠k2）窗口，重复执行步骤3至步骤6，得到另一种系数选择方案。假设第一种方案得到的低频系数为RLh1，高频系数为RH1；第二种方案得到的低频系数为RLh2，高频系数为RH2。

步骤8 比较两种方案。对于低频子带，若RLh1=RLh2，则最终的融合系数为RLh=RLh1=RLh2；若RLh1≠RLh2，则按照下面方法选择：

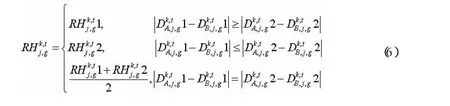
4 本文方法的过程描述

所提出的基于双窗口小波-Contourlet变换的不同聚焦图像融合算法的总体过程参见图5。

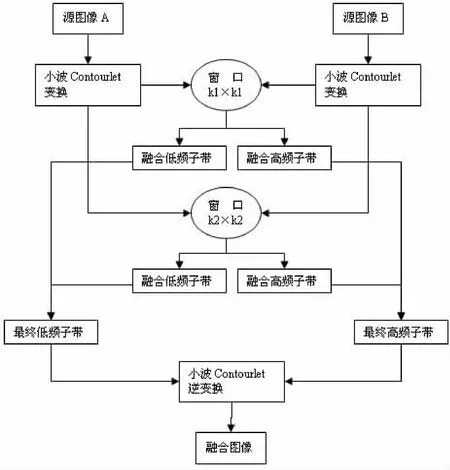
图5 本章算法框图

5 实验和性能分析

本论文实验采用MATLAB6.5软件编程实现，运行环境CPU 2.3GHz 896MB内存，操作系统Windows XP。由于在实际应用中，标准图像是不存在的，它只是人们为了实验的研究而人为地造出来，因此对于不同聚焦图像融合来说，可以通过对一副场景中所有物体都清晰的图像进行模糊处理，通过模糊图像的不同部分得到不同的原始图像，而原来清晰图像就作为标准图像。本文实验图像采用的是美国Lihigh大学提供的典型不同聚焦图像融合实验图像。

图6是对clock图像分别采用小波变换 (WDT)、Contourlet变换 (CT)、本文算法三种算法进行融合实验的结果。实验用图clock图像已经经过严格配准，512×512像素，256灰度级。低频子带采用区域能量法作为融合规则，高频子带采用区域方差法作为融合规则，并且都是采用3层分解方式。

图6 clock图像融合实验结果

图7 clock图像融合实验结果局部图

表1 clock融合结果评价参数比较

从主观视觉效果上看，图6(d)的小波变换法算法得到的融合效果较模糊，而且在图像边缘处出现明显的虚影现象，如大时钟的上边缘处，见图7(d)所示；图6(e)的Contourlet变换融合效果相对于小波变换算法有一定的改善，但有的边缘处理的效果还是不够理想，也出现了部分虚影想象，如图7(e)所示。图6(f)是本文算法融合结果，图像的边缘平滑，没有出现虚假轮廓，融合图像画面较清晰，如图7(f)的局部图所示。为了客观地评价融合图像的质量，选用均方根误差和相似性度量作为评价指标，对三类融合算法进行性能分析。如表1所示，采用CT变换法比小波变换法得到的评价指标好，特别是均方根误差相差较大，说明CT变换比小波变换在细节表现方面更突出，而本文算法得到的均方根误差和相似性度量均优于CT变换，说明采用本文算法得到的融合图像携带的信息量更多。

6 结论

WBCT变换作为一种新的图像多尺度几何分析工具，具有多分辨率性、时频局域性、方向各异性，相对于小波变换仅具有三个方向特征，能够有效地捕捉图像各个方向的特征，特别是对奇异曲线能够实现有效的逼近。因此，将WBCT变换应用到图像融合中，将会得到比小波变换更有效的融合性能。

本文提出一种基于双窗口WBCT变换的不同聚焦图像融合算法。首先采用小波变换对图像进行分解，然后采用方向滤波器组对高频子带进行方向滤波。低频子带根据局域能量法进行融合，高频子带根据局域方差进行融合。考虑到单窗口尺寸对图像特征有影响，本文采用两类窗口尺寸，通过比较两类窗口尺寸下的融合图像的WBCT变换结果，得到最终的融合图像的WBCT变换，然后采用逆WBCT变换得到融合图像。WBCT变换比小波变换和CT变换优异的地方在于：首先是用小波变换取代拉普拉斯金字塔，可以避免拉普拉斯金字塔产生的冗余；其次是高频子带具有更多的各向异性，更充分地描述了图像的细节信息，为图像融合提供了可靠的信息。实验证实，本文算法的融合性能优于小波变换、CT变换。本文提出的融合算法针对窗口大小对图像特征统计量的影响，采用双窗口比较融合策略，能够有效地减少这种影响对融合图像质量产生的影响。

[1]M NDo,VetterliM.Contourlets:a directionalmulti-resolution image representation[A].Processing of IEEE InternationalConferenceon Image Processing Rochester,2002:357-360.

[2]M NDo,VetterliM.The contourlet transform:an efficientdirectionalmulti-resolution image representation[J].IEEE Transactionson Image Processing,2005,14(12):2091-2106.

[3]EslamiR,Radha H.Waveletbased contourlet transform and its application to image coding[A].IEEE International Conference on Image Processing,2004:3189-3192.

[4]MallatS,HwangW L.Singularity detection and processingwith wavelets[J].Information Theory,IEEE Transactions on,Volume:38,Issue:2March 1992，38(2):617-643.

[5]Bamberger RH,Smith M JT.A filterbank for the directionaldecomposition of images:theory and design[J].IEEETrans Signal Pico,1992,40(4):882-893.

[6]M.N.Do,M.Vetterli.Pyramidaldirectional filterbanksand curvelets[C].IEEE InternationalConference on Image Processing(ICIP),Thessaloniki,Greece,October2001:158-161.

[7]Mallat,S.Zero-crossingsofawavelet transform[J].Information Theory,IEEETransactionson,1991，37(4):1019-1033.

[8]吴体瑞,吴小俊.一种基于区域和Contourlet变换的多聚焦图像融合新算法[J].中国体视学与图像分析,2007,12(2):98-104.

[9]梅益君,王元庆.基于点扩散函数的多聚焦图像融合方法[J].计算机工程,2007,19(10):193-195.

An Algorithm for Image Fusion by W avelet-Contourlet Transform and DoubleW indows

Gao Xueni
(School of Computer,Electronics and Information of Guangxi University,Nannning 530004，China)

An algorithm for image fusion by wavelet-contourlet transform and double windows is proposed in this paper.Firstly,the image is decomposed bymeans of wavelet-contourlet transform.Secondly,the characteristic value of coefficients is calculated in two windows of different sizes:the value of low-frequency sub-band calculated through regional energy and the value of high-frequency sub-band calculated through regional variance.Meanwhile,the characteristic values under the two sub-bands in the double windows are compared respectively and the results of the comparison are taken as the selection basis of fusing the coefficients.Finally,a fused image is obtained through inversed wavelet-contourlet transform.Simulation experiments indicates that,in the same type of feature selection,the fusion effect of thismethod is better than that ofwavelet transform and contourlet transform and leads to better fused images.

wavelet transform;contourlet transform;image fusion;double windows

TP391

A

1673-8535(2010)03-0001-09

高雪妮（1984-），女，广西来宾人，广西大学计算机与电子信息学院硕士研究生，主要研究方向：图像处理。

（责任编辑：高 坚）

2010-03-01

广西自然科学基金资助项目(0832283)；梧州学院基金资助项目(2008D011)