2010年浙江省数学高考文科试题第20题透析
●金雅芳 (春晖中学 浙江上虞 312353)
从2010年浙江省数学高考文科立体几何试题中的立意可以看出,点、线、面之间的关系仍然是考查的重点.就数学学科而言,最大的特点是在于连结空间形式和数量关系,因此考查空间想象力一直得到高考命题者的青睐.2010年考纲中明确说明点、线、面之间的位置关系的学习要做到如下3点:(1)理解空间直线、平面位置关系的定义,并了解如下推理依据,即“4个公理”和“1个等角定理”.(2)以立体几何的上述定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定,并熟练掌握线面平行、线面垂直、面面平行、面面垂直等的判定定理以及性质定理.(3)能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题,如证明线面平行、线面垂直、面面平行、面面垂直;求解一个距离、二类图形及3个角,即一个距离——点到平面的距离,二类图形——凸多面体及翻折图形,三类角——异面直线所成的角、线面角及二面角的平面角.
题目如图 1,在平行四边形ABCD中,AB=2BC,∠ABC=120°.E为线段 AB的中点,将△ADE沿直线DE翻折成△A'DE,使平面A'DE⊥平面 ABCD,F为线段A'C的中点.
(1)求证:BF∥平面A'DE;
(2)设M为线段DE的中点,求直线FM与平面A'DE所成角的余弦值.
(1)证明 取DC的中点H,连结BH,HF.由H为中点,可得
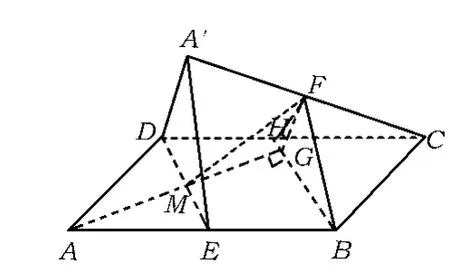
图1
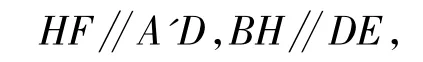
因此平面A'DE∥平面BHF,即BF∥平面A'DE.
(2)解 由第(1)小题可得,平面A'DE∥平面BHF,因此直线FM与平面A'DE所成角即为直线FM与平面BHF所成的角.又由平面A'DE⊥平面BCD,得平面BHF⊥平面BCD.连结AM并延长交BH于点 G.根据题意,可得 MG⊥平面 BHF,即∠MFG为直线FM与平面BHF所成的角.设AB=2BC=2,可得
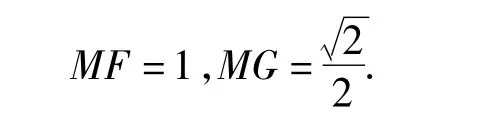
从学生对本题的解答情况看,得分相对较低.主要体现在2个方面:一是直接过点F作平面A'DE的垂线难度大,若采用上面的求解,面面平行来转化角度则不容易想到;二是用空间向量处理试题,坐标系不很常规,致使解答情况不理想.介于上述学生的状况及试题情况,在立体几何复习时应着眼基础,即立足基本定理;应放眼图形,即紧抓图形特色,这样才能做对、做活试题.
由上面的求解可以发现,高三数学复习,应注意以下几点.
1 基础教学——稳扎稳打
对立体几何的复习,首先要强化基础知识的训练,确实掌握基本概念、性质、定理、公理、推论等,同时要掌握这些定理在不同题目中的用法,理解它们的个性和通性,在此基础上突出重点、强调中心问题,找到解各种题目的突破口,提高解题能力.
其中一项重要的能力是“画图”.高考卷中立体几何的小题一般都不给出图形,而大题中所给的图形又往往需要添加辅助元素,因此从某种意义上说,作出一个好图等于题目解决了一半!训练中要做到:(1)会画——根据题设条件画出适合题意的图形或画出自己想作的辅助线(面),作出的图形要直观、虚实分明;(2)会看——根据题目给出的图形,想象出立体的形状和有关线面的位置关系;(3)会用——对图形进行必要的分解、组合,或对某部分进行平移、翻折、旋转、展开或割补等.
同时,复习过程中还需注意其他板块的基础知识在立体几何题中的运用,譬如绝大多数求解型题最后都需要在构建好的平面图形(尤其是三角形)中才能解决,因此诸如像平面几何的相关知识、三角函数、正余弦定理等就必不可少了.
2 重点把握——求精求实
近几年的高考题比较注重求问形式的多元化,但问题最终的落脚点无外乎是证明平行或垂直、求解角度或距离,而解决的方法也主要集中在几个常见的形式上.
例如,求证空间中某直线和某平面的平行关系,要么采用线面平行的判定定理——在该平面中找到一条和该直线平行的直线(利用中位线或平行四边形),要么采用面面平行的性质定理——构造过该直线与该平面平行的平面.
再如,利用三垂线求作二面角的平面角,一般只要在其中一个半平面内找到一点P,过它的一个平面和另一半平面相交得到交线,再过点P作此交线的垂线,垂足即为点P的射影.之后过此射影作二面角的棱的垂线并连结垂足和点P,平面角即会出现.这种方式还可用在求解线面角、点面距等问题中.
3 规律探索——讲准讲活
立体几何解题中常有明显的规律性,因此在复习中必需对概念、定理、题型、方法等进行总结、归类,进而建立知识框架和网络,弄清各概念之间的包含关系,理清定理的来龙去脉和相互转化的过程,从内涵和外延上区分容易混淆的各个概念,从条件、结论和使用范围上去区分容易混淆的各个定理.另外,空间向量的引入为我们开辟了一条新的道路,尤其在求解空间角与距离的问题中,向量法极具可操作性、规律性,并具有一定的优势.只要能够建立恰当的坐标系、掌握好“法向量”的求解方法并学会各种角与距离的向量法求解公式,问题一般就不难解决了,但必须要保证运算的精准!
2010年的文、理科立体几何试题均是图形翻折问题,这让一部分学生“投降了”.一方面试题的难度增加,但更大一部分是学生在考试中遇到难点及不顺,面对新题及困难时的心态调整和战胜困难的勇气等非智力因素还有待提高.对我们而言,今后数学的教与学任重而道远.

