2 0 1 0年数学高考立体几何试题评析
●骆永明 (稽山中学 浙江绍兴 312000)
立体几何是高考必考内容,试题一般以“两小题一大题”的形式出现,分值在20分左右,考查难度一般为中等.简答题所处位置基本上在前3道,有承上启下的作用.另外,笔者在认真统计与分析近几年的高考试题后发现,立体几何问题的考查已经突破了传统的框架;在命题风格上,正逐步由封闭性向灵活性、开放性转变.因此,进一步把握复习的重点、提高复习效率,从而快速地突破立体几何的难点是高考复习过程中必须认真考虑的问题.
1 《课程标准》和《考试说明》对本专题的教学要求
1.1 考试内容
三视图;球、柱、锥、台的表面积和体积的计算;空间位置关系的判断与证明;空间角、距离的求解.
1.2 考试要求
(1)能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,会用斜二测法画出它们的直观图.能识别三视图所表示的空间几何体;理解三视图和直观图的联系,并能进行转化.
(2)会计算球、柱、锥、台的表面积和体积(不要求记忆公式).
(3)以公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定;会用几何法和向量方法证明有关直线和平面位置关系的有关命题.
(4)理解异面直线所成角、直线与平面所成角、二面角的概念;会用几何法和向量方法解决异面直线所成角、直线与平面所成角、二面角的计算问题.
2 命题特点
从立体几何所考查的知识点可以看出:与前几年相比仍着眼在一个“稳”字上,具体体现在以下几个方面:
(1)题量、分值、难度基本上保持相对稳定.
每份试题基本上以“两小题一大题”或“一小题一大题”的形式出现,分值在20分左右.选择题、填空题考查的知识点主要涉及到空间线面位置关系的判断、空间角和距离的求解、体积与面积的计算、三视图和几何体的接切问题等.解答题的考查形式仍然注重在一个具体的立体几何模型中考查线面位置关系.
(2)考查题型、内容不避热点.
以空间几何体为载体的线面关系的判断、推理和论证,尤其是线线、线面、面面的平行和垂直的判断、推理和论证;三视图体积与面积的计算;空间角和距离的计算,几何体之间的“接”与“切”等问题历来是高考数学的重点和热点,也是2010年高考命题的主流.
(3)考查立体几何的基本数学思想.
立体几何在考查学生的观察能力、思维能力和空间想象能力方面具有独特的作用,历来是高考的重点内容之一.转化与化归思想、逻辑推理能力、数形结合思想、割补思想等数学思想在2010年的高考立体几何试题中体现得淋漓尽致.
(4)继续正视文、理科学生的差异.
在对立体几何这部分内容的考查上,基本上采用“姊妹题”、“相同题不同考查顺序”等来区别对待.在简答题上,文科突出考查直观感知与简单推理论证;而理科对空间想象能力、逻辑推理能力的考查要求较高.同时,理科大题在设计中仍然坚持“几何法”与“向量法”兼顾,统筹安排、有机结合、相得益彰.
3 亮点扫描
3.1 “动态折叠”,立体几何常考常新
在近几年的高考试题中,经常出现一些有关立体几何中的翻折、旋转等“动态折叠”问题.它们立意新颖、动态变换、注重创新,加强了试题的开放性与探究性,同时也给学生解决问题提供了更广阔的思维空间,能有效地检测学生的直观感知、观察发现、空间想象、推理论证、运算求解与分析和解决问题等能力,具有很好的考查功能和导向作用.
例1 如图1,在矩形ABCD中,点E,F分别在线段AB,AD上,AE=EB=AF=2FD=4.沿直线3EF将AEF翻折成A'EF,使平面A'EF⊥平面BEF.
(1)求二面角A'-FD-C的余弦值;
(2)点M,N分别在线段FD,BC上,若沿直线MN将四边形MNCD向上翻折,使点C与点 A'重合,求线段 FM的长.
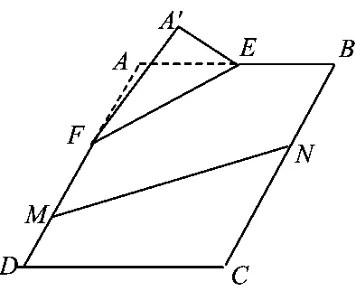
图1
(2010年浙江省数学高考理科试题)
解(1)坐标法:按如图2所示建立坐标系,面A'FD的一个法向量为n=(0,-2,),面 BEF的一个法向量为 m=(0,0,1),则
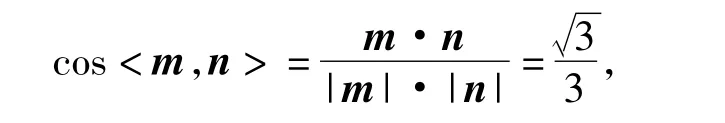
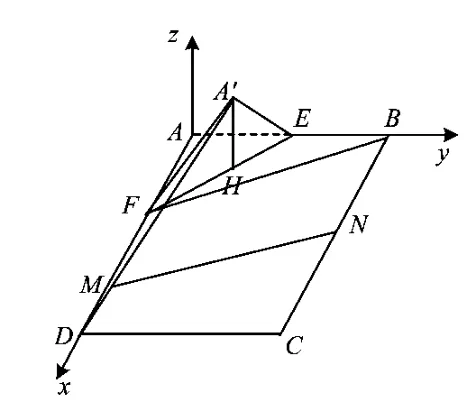
图2

图3

评注近3年的浙江省数学高考试题都考查了“动态折叠”问题,特别是2010年从学生极为常见的长方形翻折着手,把2次翻折后改造成颇有难度的立体几何问题,使考生似曾相识,又不乏新意.解决该题的关键是要求学生清楚折叠前后哪些量发生了变化,哪些量没有发生变化.
3.2 关注知识的交汇,实现融会贯通
例2 到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是 ( )
A.直线 B.椭圆
C.抛物线 D.双曲线
(2010年重庆市数学高考理科试题)
解如图4,构造一个单位正方体,以A为坐标原点,AB为x轴,AD为y轴建立直角坐标系.设点P的坐标为(x,y),由题意得

可知轨迹为双曲线.故选D.
评注以立体几何为载体,重点考查如何用坐标法或定义法求动点轨迹方程,目的是考查学生的空间想象能力及如何用坐标法解决立体几何中求轨迹的问题,体现几何问题代数化的思想方法.
同时2010年福建省数学高考理科试题第18题与几何概型交汇,考查了直线与直线、直线与平面、平面与平面的位置关系;还考查了空间想象能力、运算求解能力、推理论证能力,考查数形结合思想、化归与转化思想、必然与或然思想.
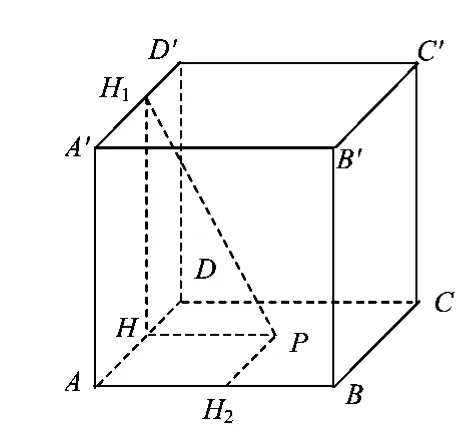
图4
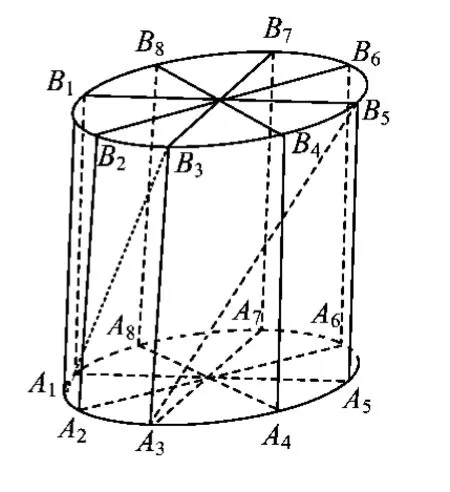
图5
3.3 强调知识的应用,注重综合能力的考查
数学源于生活又寓于生活,课程标准特别强调学生对数学的实践运用能力.以立体几何为背景的实际应用题逐渐被人们重视.2010年上海市数学高考理科试题第21题以圆柱形的灯笼为背景设计了立体几何问题,具有很大的现实意义,考查了学生解决数学问题的方法、策略、能力,是现代教育对数学教育的迫切要求,充分体现了教育改革的不断发展与高考改革的逐步深化.
例3 如图5所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,骨架把圆柱底面8等份,再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
(1)当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米);
(2)在灯笼内,以矩形骨架的顶点为点,安装一些霓虹灯,当灯笼的底面半径为0.3米时,求图中2条直线A1B3与A3B5所在异面直线所成角的大小(结果用反三角函数表示).
(2010年上海市数学高考理科试题)
解(1)略.
(2)建立坐标系易得
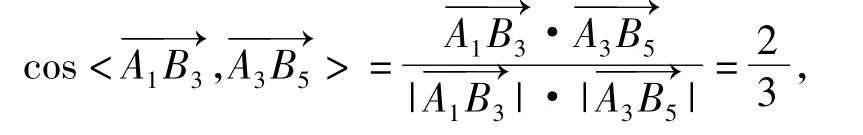
评注本题以圆柱形灯笼为载体,考查二次函数的实际应用、异面直线所成角的概念与求法.该题引导学生深入社会实际,关注生活,在加强数学应用意识的同时,考查了空间想象能力.立体几何板块难度比2009年有所上升;考查了学生提炼数学模型、应用数学的能力.
4 复习建议
(1)立足一本两纲,回归课本,狠抓双基.
教师需对《考试大纲》与《教学大纲》进行深入研究,立足本专题的基础知识和基本方法的复习.重视基础知识教学,落实点、线、面位置关系的判断以及相关概念、定理、性质;熟练掌握课本中概念、定理的种种用途;重视提高学生的空间想象能力,培养学生识图、画图和对图形的理解能力.同时要让学生回归课本,重视课本的例题与习题,使数学教学回归到本源上来.
(2)建议对新教材中新增内容进行关注.
新教材中的立体几何与传统的立体几何相比,发生了一定的变化.其中在必修2中学习的立体几何初步主要是依托三视图来提升学生空间想象力的.同时,对于这些模型截去一个面所形成的多面体的三视图也应该引起关注.例如,2010年北京市数学高考理科试题第3题.对于一些不规则几何体,若采用割补法,则往往能起到化繁为简、一目了然的作用.
(3)重视数学思想方法的教学,特别是化归的思想.
(4)建议加强对向量公式的理解.
用传统的方法解立体几何题往往需要烦琐的分析、复杂的计算.而用向量法解题思路清晰、过程简洁.对立体几何的常见问题可以起到化繁为简、化难为易的效果.利用向量可以解决立体几何中点、线、面的各种位置关系问题,但在具体问题中有许多需要注意的问题.
例如,已知二面角 α-l-β,m,n 分别为面 α,β 的法向量,则二面角的平面角θ的大小与2个法向量所成的角相等或互补,即θ=<m,n>或θ=π-<m,n>.但如何判断二面角的平面角和法向量所成的角的关系,通常有2种方法:①通过观察二面角是锐角还是钝角,再由法向量所成的角求之;②通过观察法向量的方向,判断法向量所成的角与二面角的平面角是相等还是互补.
又如直线和平面所成的角用向量求解时,法向量和直线所成的角与直线和平面所成角的关系都是需要引起注意的问题,学生很容易犯错误.

