2010年数学高考中有关计数原理试题的评价
●徐国君 李惟峰 (杭州外国语学校 浙江杭州 310023)
计数问题是数学中的重要研究对象之一.分类加法计数原理、分类乘法计数原理是解决计数问题的最基本、最重要的方法,它们为解决很多实际问题提供了思想和工具.下面笔者结合2010年数学高考试题从以下几个方面加以说明.
1 新旧课程的对比分析
在新课程中,学生将学习计数基本原理、排列组合、二项式定理及其应用,了解计数与现实生活的联系,会解决简单的计数问题.总的教学目标是通过实例,总结分类加法计数原理、分类乘法计数原理;能根据具体问题的特征,选择分类加法计数原理或分步计数原理,解决一些简单的实际问题.提高学生转化问题的能力、逻辑分析能力和分类讨论思想的运用能力.
与原大纲相比,新课程对分类加法计数原理与分步乘法计数原理在内容编排上做了一些调整.特别是在处理方法上,更强调基本的计数原理,强调计数原理在实际中的应用,强调对计数原理思想的理解,避免抽象地讨论计数原理.在排列组合的教学中,新课程是将排列组合作为计数原理的应用实例来处理的,且排列组合的应用题设计的问题背景非常丰富,因此需要有较强的抽象思维能力.通过典型例题,形成典型问题的思维模式,注重常见题型与常用方法的归纳.二项式定理是组合知识与多项式知识的结合,新课程教学非常注重二项式定理的推导过程,理解特殊到一般的思维方法,培养学生的观察归纳能力、抽象思维能力和逻辑思维能力.
2 命题特点和知识类型
计数原理在高考中多以客观题的形式出现,每年有1~2道题,试题难度基本为中低档,考查学生转化问题的能力、逻辑分析能力和分类讨论的思想方法.在2010年全国各地的数学高考试卷中,可以说计数原理的考查基本沿袭了以往的风格,部分题目有一定的难度.
例1 有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”5个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人,则不同的安排方式共有_______种(用数字作答).
(2010年浙江省数学高考理科试题)
命题意图分析 这是一道典型的计数原理题,主要考查学生的分析能力、用分类讨论的方法解决问题的能力.
分析为了方便解题与分析,可以把题目的要求结合以下的表格(如表1)加以体现.

表1 各项目测试安排表
依据以上的表格可非常清晰地把这个较难的计数原理的问题加以解决:由题意在上午的测试中,在可以测试的4个项目中应该各有一名同学,且没有其他限制,因此有24种;而下午的安排要受到上午安排的影响且要求限制较多,这种情况下可以采取分类讨论的方法加以解决,经分析可以分为以下2个大类:
(1)若丁所测项目上午是“台阶”,下午是“握力”,则甲、乙、丙在上午给定排定测试项目的前提下,下午实质上就是要求与上午的测定项目全不相同,是个全错位排列问题,共有2种排列方法.
(2)若丁上午测“台阶”,下午所测项目是甲、乙、丙在上午所测项目中的一项,则有3种不同的情况.丁排定后,甲、乙、丙选择一人测“握力”有3种不同的选法,选定后依题意剩下2位同学的测试项目就唯一确定下来了.
故不同的排列方法共有
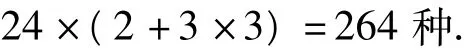
点评应该说,本题的叙述会给考生以繁琐、难理解的感觉.题目中涉及的限制条件与要求较多,往往会令考生难以下手,有较高的能力要求.从考生反馈的信息来看,本题的得分率也不是很高.值得肯定的是本题充分体现了新课程的培养目标,有很好的教学指导意义,值得一线教师的反思体会.
例2 现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机4项工作之一,每项工作至少有一人参加.甲、乙不会开车但能从事其他3项工作,丙、丁、戊都能胜4项工作,则不同安排方案的种数是( )
A.152 B.126 C.90 D.54(2010年湖北省数学高考理科试题)
命题意图 这是一道排列组合中常见的有条件的分配问题,主要考查学生的分析能力、用分类讨论的方法解决问题的能力.
分析由于题目中有5位同学,而需要从事的工作只有4项,有限制的是司机这项工作,因此选择从工作出发选人的方法,且先确定从事司机的人选.依题意必然有一项工作有2人,其他工作各1人.可分为以下2类进行讨论:
因而共有不同安排方案的种数是18+108=126种.故选B.
点评本题是一个较常规的排列组合问题,其中涉及到分类讨论、分配等常见的排列组合问题,难度适中.体现出重视基本问题、基本技能的指导思想.

(2010年辽宁省数学高考理科试题)
命题意图分析 本题是一道二项式定理题,主要考查学生3个方面的能力:(1)基本的通项求解方法;(2)二项式定理的本质应用;(3)分类讨论的思想方法的运用.



所以可以发现展开式中没有x-1这一项,即这种情况不可能.
(3)x2与 x-2抵消成常数:1 ×(-1)4=15.
综上所述,常数项为-20+15=-5.
点评本题体现了新课程中对二项式定理的教学要求,要求考生既要学会基本的解题方法和技巧——展开式的通项公式的应用,又要充分理解二项式定理推导过程的思维实质,并能把这个思维实质进行有效地迁移应用.有一定的难度,也有非常好的教学指导意义.
3 亮点扫描
(1)体现了对基本知识、基本技能的掌握.淡化过分的技巧化、模型化.
(2)题目贴近生活.充分体现了数学的真谛,即来源于生活,服务于生活,有很强的现实指导意义和生活背景.也体现了数学的人文素养和人文价值所在,给教学指明了方向.
(3)题目立意深刻,注重知识的理解.考题中无不渗透出摒弃“题海”,注重知识的理解和掌握的指导思想.
(4)题目立足基础,体现能力.在立足基础的前提下,非常讲究能力的考查.要求考生有较强的知识迁移能力.
4 复习建议
可以说,2010年高考试题充分体现了新课程对于这一部分内容的教学要求,题目有新意,既立足基本知识、基本技能,又体现了较高的能力要求,因此也给数学教师提出了新的历史使命.基于此,笔者有以下的复习建议,供同行参考:
(1)在教学中,不仅要重视每个知识结论的教学,更应注重知识发生、发展和形成过程.在指导学生解题过程中,应淡化技巧,突出通性通法的训练,引导学生对解题方法归类、概括和总结,提高学生的解题能力.
(2)注重能力培养,着眼创新意识和实践能力的提高.近几年高考试题开发了研究型、探索型和开放型等体现数学素质的能力型试题,学生要在主动探究知识、分析思考和解决问题的过程中,理解知识,掌握数学思想方法和解决问题的策略,提高能力.
(3)合理安排该模块的训练难度,把握复习的重点和热点.对于了解层次要求的知识点要严格控制难度;掌握层次要求的内容既可以出难题,也可以出中等题与容易题.作为新的高考热点,当然应成为复习的重点.
(4)要认真学习《学科指导意见》,确定复习的内容和重点.只有紧扣《学科指导意见》,才能科学、合理地安排复习,从而提高效率.以不变应万变,构建知识网络,集中精力破解学习中的疑难问题.

