用最小二分法进行已知两端点及半径圆弧测设
赵崇山
施工中常会遇到一些圆弧造型的放线工作,一般情况下,圆弧的起点、终点、半径设计中都会给定,而扫圆弧半径由于现场条件限制,如半径较长、存在障碍物甚至圆心位于空中位置,直接从圆心放圆弧并不现实。这里介绍一种简单易行的放线方法。
1 计算过程
如图1所示:已知圆弧起点 A,B,半径 R,AB直线距离L1为已知(或可现场内测量得知)。
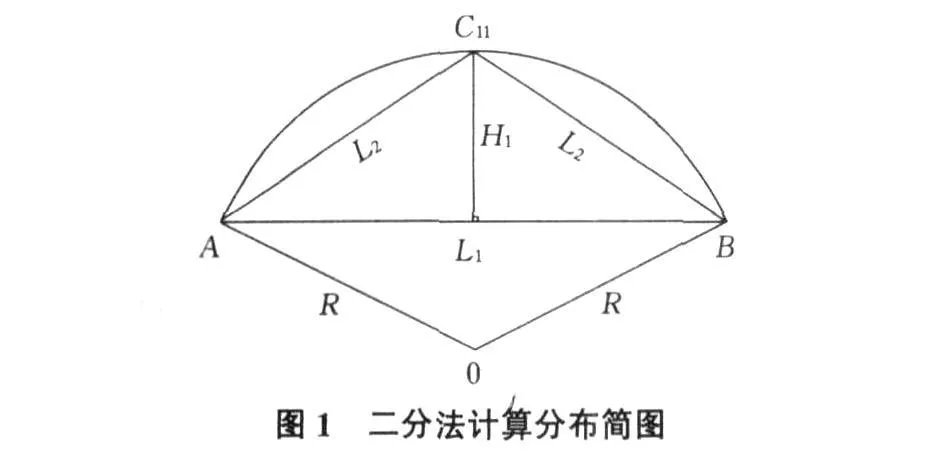
其矢高为:
H1=R-sqrt(R×R-L1×L1/4)(圆心角不大于180°时)。
特殊的,H1=R+sqrt(R×R-L1×L1/4)(圆心角大于180°时)。
作 AB垂直平分线,量H1得 C11点。
则 AC11=C11B=L2,L2=sqrt(L1×L1/4+H1×H1)。
依次类推,得各最小二分点:一级点:C11;二级点:C21,C22;三级点:C31,C32,C33,C34;……i级点:Ci1,Ci2,…,Cin(n=2i-1)。 Hi=R-sqrt(R ×R-Li×Li/4)。 Li+1=sqrt(Li×Li/4+Hi×Hi)。列表1计算(可利用Excel公式计算功能)。
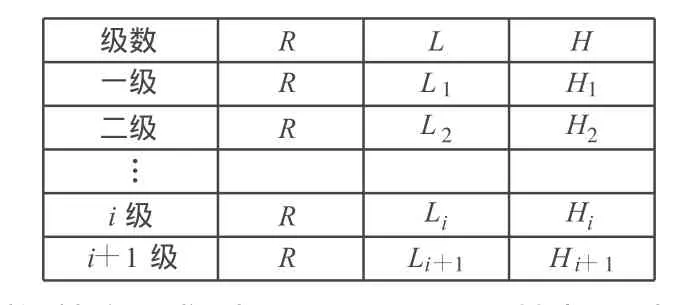
表1 二分法计算表
根据测设精度要求,直至:Hi+1<δ/2(其中,δ为规范允许偏差)。
2 操作步骤
1)测设 A,B端点。2)连线 AB为1级弦,尺量 LAB/2找出弦 AB中点,以此中点用方尺垂直弦 AB量H1,得一级点 C11点。3)连接起始点及 1级点,得2级弦(有2条),尺量 L2/2找弦中点,以各中点用方尺垂直各弦量 H2,得二级点 C21,C22点。4)重复以上步骤。5)连接起始点及1级~i-1级点得 i级弦(有2i-1条),尺量 Li/2找弦中点,以各中点用方尺垂直各弦量 Hi,得i级点Ci1,Ci2,…,Cin(n=2i-1)点。6)测设点数统计见表2。7)此时,可光滑连接起始点及1级~i级各二分点[也可以直(i+1级弦)代弧连接],得到所求圆弧放样线(见图2)。

表2 测设点数总统计表

3 举例
例:已知圆弧半径R=19.67 m,起始点 A,B距离为 8 m,则各级数据计算如表3所示。
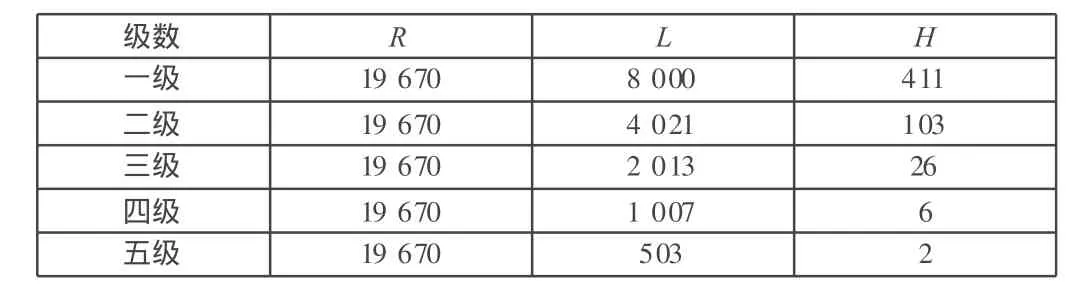
表3 各级数据计算表 mm
从表3中数据可以看出,测设点收敛至四级时,以弦代弧所得连线(5级弦)产生理论误差应为五级时对应 H5=2 mm<8/2=4 mm(以混凝土结构为例,建筑施工质量验收规范允许轴线偏差为8 mm)。

表4 测设点数统计表
1)测设 A,B端点,复核 AB距离8 000 mm。2)连线 AB,尺量8 000/2=4 000 mm,找出弦 AB中点,以此中点用方尺垂直弦AB量H1=411 mm,得1级点 C11点。3)连接起始点及1级点,得2级弦(有2条),尺量4 021/2=2 010.5 mm找弦中点,以各中点用方尺垂直各弦量 H2=103 mm,得2级点 C21,C22点。4)连接起始点及1级,2级点,得3级弦(有23-1=4条),尺量2 013/2=1 006.5 mm找弦中点,以各中点用方尺垂直各弦量 H3=26 mm,得3级点 C31,C32,C33,C34点。5)连接起始点及 1级,2级,3级点,得4级弦(有 24-1=8条),尺量 1 007/2找弦中点,以各中点用方尺垂直各弦量 H4=6 mm,得4级点 C41,C42,C43,…,C48点。6)测设点数统计见表4。7)此时,光滑连接起始点及1级~4级各二分点(也可以直(5级弦)代弧连接),得到所求圆弧放样线。
4 结语
此方法优点为:1)收敛速度快:常见建筑工程中圆弧测设,一般只需3级~5级即可达到规范要求。2)测设工具简单:一般只需直尺、线绳即可。3)测设精度高:选择合适的级数,即可达到要求的精度。其缺点是测设点多,且随着级数增多,其增加测设点数成倍增长,如上例四级总点数达到15点。但由于其计算公式化,操作的简单性,且方法通用性强,在已知两端点及半径的圆弧放样工作中不失为一种值得优选的测设方法。

