高速列车与铁路简支梁桥动力相互作用研究
胡希冀 张 明 张利宁
随着行车速度的不断提高,交通密度的不断增加,荷载的不断加重,交通车辆与结构的动力相互作用问题越来越受到人们的重视。特别是近年来越来越多的高速铁路相继投入运行。一方面,高速运行的车辆对所通过的结构物产生动力冲击作用,直接影响其工作状态和使用寿命;另一方面,结构的振动又对运行车辆的平稳性和安全性产生影响[1]。常见车辆的简化模型有以下几种:1)将车辆以荷载形式简化为集中力,在梁上移动;2)将车辆简化为移动质量,在梁上移动;3)将车辆以荷载形式简化为移动的简谐力,在梁上移动;4)将车辆简化为移动的弹簧质点,在梁上移动。这几种简化方法中,以移动弹簧上的质量模型最为合理,但也最为复杂,而将车辆看作移动的集中力即移动荷载和移动质量这两种简化方式最为简单[2]。本文通过建立移动车轮加簧上质量模型,采用有限元软件ANSYS来研究和比较不同工况下车辆在简支桥梁上运行引起的车桥动力响应。
1 模型的建立
用移动车轮加簧上质量模拟车辆匀速通过跨度为32 m简支梁的情形,采用ANSYS软件建立相应模型,对桥梁的动力响应进行仿真计算。计算中,模型忽略桥梁粗糙、不平顺的影响,不考虑外界风载及地震荷载的影响,不考虑车的初始状态,即认为车辆在理想的状态下运行通过桥面。
本文采用二维梁单元Beam3来模拟桥梁,划分的单元数由荷载的移动速度和桥梁长度来决定。单元长度ΔL=L/N,其中,L为桥梁的跨长;N为划分的单元数。这样,荷载在单元之间的运行时间(即从i节点变化到i+1节点)为 t=ΔL/v,其中,v为移动荷载的速度。计算时,划分单元数N=100。
在计算结构动态响应时,时间步长Δt的选取是否合适,对计算结果能否反映结构响应特征产生很大的影响。如果时间步长Δt太大,有可能得到完全失真的响应曲线[3]。在如图1所示的响应曲线中,如果步长不当,将会得到如图1中虚线所示的错误的响应曲线。
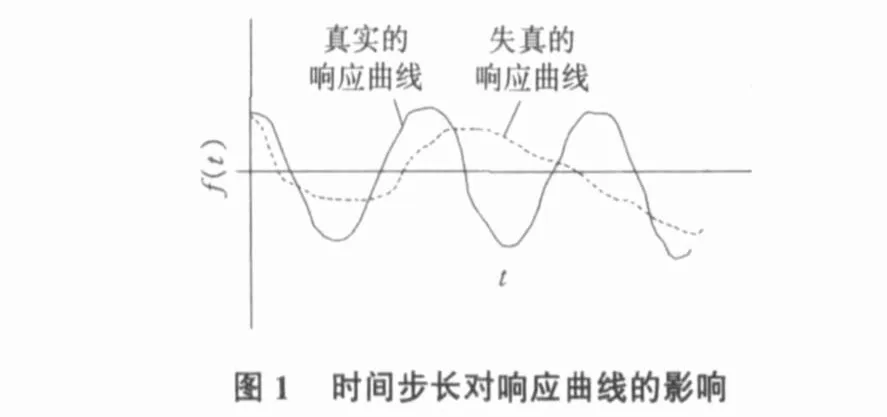
时间步长的选取,应根据动态响应的振动周期频率来确定。由于三点确定一条抛物线,因此为了真实描述结构动态响应,在一个振动周期中应至少取5个点。如果设T为结构振动的周期,f为结构振动的频率,那么结构动态响应计算的时间步长应取为:

本文采用桥梁模型基准数据如下:简支梁跨度 L=32 m,材料为50号混凝土,弹性模量E=3.5×1010N/m2,箱形断面,断面高度2.8 m,断面宽度 13 m,截面面积 A=8.29 m2,惯性矩 I=8.6 m4,密度ρ=2 500 kg/m3,本文研究的是高速车辆与桥梁的动力响应,采用的基准车速为300 km/h。以5 km/h的车速作为静态车速。
2 数值模拟及结果分析
2.1 车速对跨中挠度的影响

表1 不同速度下桥梁跨中最大竖向动挠度
通过表1中的数据可以得到,在速度比较低的情况下,跨中节点的动挠度随着移动车辆速度提高而增加的比较少,但是当速度提高到一定程度时,跨中节点的动挠度增加非常大。本例中,当速度为50 km/h时,跨中节点的动挠度增量为静态车速动挠度的2.09%。当速度为100 km/h时,跨中节点的动挠度增量为静态车速动挠度的4.17%。当速度为200 km/h时,跨中节点的动挠度增量为静态车速动挠度的16.60%。当速度为300 km/h时,跨中节点动挠度增量为静态车速动挠度的15.55%。可以看出,随着车速的提高,跨中节点的动挠度增量是十分明显而且是不可忽略的。但是从上面的数据可以看出,动挠度的增量并不是与车速成正比的。图2给出了桥梁在不同速度作用下的动力系数曲线。速度以10 km/h开始,然后以10 km/h递增,直到300 km/h。前面的结论只是取了图中的四个特殊的数据点,即速度为50 km/h,100 km/h,200 km/h,300 km/h,从图2可以看到,这四点并不符合一种简单上升的规律。从更详细的速度影响曲线来看,用典型工况计算所得的结果忽略了许多细节性的变化规律,速度对桥梁动力系数的影响应该是一个比较复杂的过程,并非跨中节点动挠度随着移动荷载速度的提高而简单的增大,而应该是幅值和周期都在增大的类似于半正弦波式的曲线。
2.2 阻尼对跨中挠度的影响

表2 不同阻尼下桥梁跨中最大竖向动挠度
由表2可知,对于高速运行的车辆,随着梁上阻尼比的增加,梁上节点的动挠度逐渐减小。另外,随着梁上阻尼比的增加,各节点发生最大动挠度时荷载所在地位置逐渐后移。
图3给出了桥梁在不同阻尼比下的竖向动挠度情况,结构阻尼比变化范围为0.01~0.08。从图3中我们不难看出最大动挠度与结构阻尼比的关系已不再是线性的而变为非线性的。结构阻尼比越大,跨中节点的最大动挠度越小。

2.3 刚度对跨中挠度的影响
本文采用提高材料弹性模量的方法来提高结构的刚度,弹性模量变化范围为0.5×1010N/m2~9.5×1010N/m2。
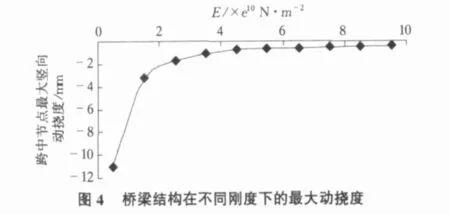
对于高速运行的车辆,随着梁刚度的增加,跨中节点的动挠度逐渐减小。动挠度曲线的形式也是随着刚度的提高变得越来越平缓。另外,可以发现,随着梁刚度的增加,跨中节点的动挠度曲线越来越接近,跨中节点的最大动挠度相差越来越小,这也说明,仅仅靠提高结构刚度的办法来控制结构的振动是不合理也不经济的。表3详细记录了刚度变化时桥梁跨中节点的最大竖向动挠度。从表3中我们也可以很明显的发现,在刚度不大时,提高结构的刚度可以有效的控制结构的最大动挠度,但是随着结构刚度的不断增大,这种限制作用越来越不明显。

表3 不同刚度下桥梁跨中最大竖向挠度
图4表示了结构弹性模量变化时桥梁跨中节点的动挠度曲线。可以明显的发现:桥梁结构的动挠度和桥梁的刚度不是简单的线性关系,在一定范围内提高结构的刚度可以有效的控制结构的振动。
3 结语
本论文采取了数值模拟计算的研究方法。对移动车轮加簧上质量作用下桥梁的动态响应做了分析研究。通过ANSYS软件对车—桥耦合系统的动态模拟,得到桥梁的动力响应和车速、结构阻尼比以及结构刚度的关系,通过数据分析得出如下结论:
1)相对中、低速行驶的列车,高速行驶的列车将使桥梁的竖向挠度有明显增加。2)移动弹簧质点作用下的动挠度曲线是以一定的频率围绕静挠度线的一种类正弦波动。随着速度的增加,波动的幅值越来越大。3)跨中节点动挠度并不是随着车辆速度的提高而简单的增大,而应该是幅值和周期都在增大的类似于半正弦波式的曲线。4)梁上阻尼对控制结构跨中挠度的影响不是很大,但是适度提高结构阻尼可以在一定程度上抑制车桥振动。
[1] 夏 禾,张 楠.车辆与结构动力相互作用[M].北京:科学出版社,2005.
[2] 曹雪琴,刘必胜.桥梁结构动力学[M].北京:中国铁道出版社,1987.
[3] 卿启湘.高速铁路无碴轨道一软岩路基系统动力特性研究[D].湖南:中南大学,2005.

