基于中心差分扩展卡尔曼滤波的电源频率估计

付 巍,朱 岩,付军立,侯 毅

(中国航空工业集团公司北京长城测试计量技术研究所,北京 100095)

0 引言

随着电子技术的发展,在飞机上安装了越来越多的用电设备,一些用电设备的非线性负载特性以及交流电压调制、频率调制等因素的影响,使电路中的实际交流电压发生畸变,飞机供电系统实际工作时,电路中的交流电压包含基波和谐波成分。有效、可靠的对电路中交流电压的基频和谐波成分的估计和监控对于供电系统控制、电力质量监视和发电机保护都有重要的意义。

许多算法被研究出来,用于交流电压基波频率的估计和谐波频率的分析。在这些算法中,卡尔曼滤波算法(KF)得到了广泛的应用[1]。对于观测量是状态变量的线性函数的情况,卡尔曼滤波算法可以得到状态变量的最优估计,但对于观测量是状态变量的非线性函数的情况,卡尔曼滤波算法将产生很大的误差。扩展卡尔曼滤波算法和无迹卡尔曼滤波算法是解决这一问题的两种有效的算法,扩展卡尔曼滤波算法将观测方程进行泰勒级数展开,去掉二阶以上的高阶项,使非线性的观测方程线性化,其优点是运算速度快,实时性强,但估计精度较低[2]。无迹卡尔曼滤波算法在目标运动状态的估计值附近进行确定采样,得到一些采样点,这些采样点被称为Sigma点。无迹卡尔曼滤波算法不同于扩展卡尔曼滤波算法之处在于无迹卡尔曼滤波算法不是对非线性函数的近似,而是对状态随机变量分布的近似,它使用真实的非线性模型,其优点是估计精度高,但运算速度慢,实时性不强[3]。为了提高飞机供电系统中交流电压基波频率估计的精度,同时减少计算复杂度,增强算法的实时性,采用中心差分的方法计算扩展卡尔曼滤波算法中非线性函数的一阶导数,形成中心差分扩展卡尔曼滤波算法。

1 飞机供电系统中交流电压信号数学模型

在三相电路中,对于任意一组不对称的三相向量,可以分解为三组三相对称的向量,当选择A相作为基准相时,三相电压向量与其对称分量之间的关系为[4-6]:

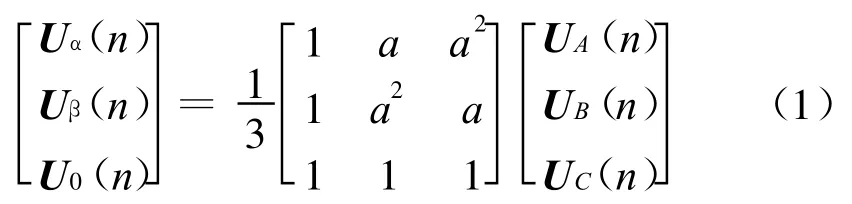
式中 ,a=ej2π/3;a2=e-j2π/3;1+a+a2=0;a3=1;U A(n)、U B(n)、U C(n)为 三 相 电 压 向 量;Uα(n)、Uβ(n)、U0(n)分别为A相电压的正序、负序和零序分量。

在飞机供电系统中,交流电压信号包含基波和谐波成分,三相电压系统的离散傅里叶级数形式可被表示为:

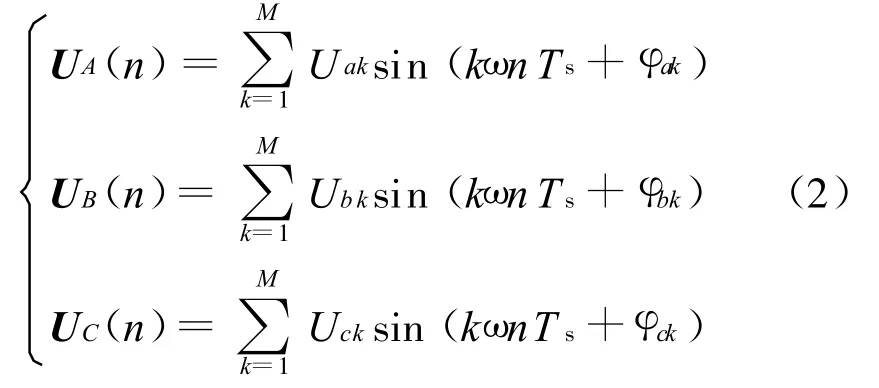
Uak、Ubk、Uck分别为三相电压k次谐波的峰值;φak、φbk、φck分别为三相电压k次谐波的相位;kω为k次谐波电压的角频率,M表示电压的谐波次数,Ts表示采样时间。

三相电压系统k次谐波电压可以用指数形式表示为:

¯UAk=Uakejφak;¯UBk=Ubkejφbk;¯UCk=Uckejφck;则三相电压系统k次谐波电压的正序和负序瞬时值对称分量分别表示为:

由式(1)、式(2)和式(3)可得:

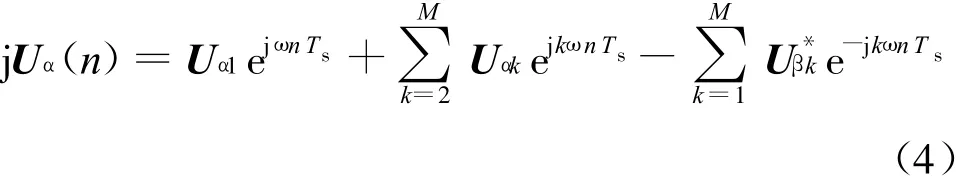
式中,U*βk表示三相电压系统k次谐波电压的负序瞬时值对称分量的共轭。式(4)包含有基频电压正序对称分量,可以作为对飞机供电系统测量时的测量方程。测量方程是一个非线性的方程,需要使用能够解决非线性方程的滤波算法对方程中的特性参数进行估计。

2 基于中心差分的扩展卡尔曼滤波算法

扩展卡尔曼滤波算法精度不高是因为在将观测方程的非线性函数线性化时进行泰勒级数展开,只保留一阶项,而略去了一阶以上的高阶分量。如果在将观测方程的非线性函数线性化时保留一阶以上的高阶分量,就可以提高扩展卡尔曼滤波算法的精度,中心差分扩展卡尔曼滤波算法就是基于这一思想提出的。

2.1 理论分析

采用多项式近似技术和一阶中心差分法计算非线性函数的偏导数,具有二阶非线性近似的能力[7-8]。

非线性函数 y=f(x-u)和 y=f(x+u),分别在x处的泰勒级数展开式为:

式中,o1(u2)和o2(u2)表示泰勒级数展开式的二阶以上的高阶分量。

则由式(5)和式(6)得到中心差分的表达式:

式中,o(u2)=(o2(u2)-o1(u2));u表示中心差分的步长。

从式(7)可以看出,f(x+u)-f(x-u)/2u不仅包含非线性函数 f(x)的一阶导数f′(x),还包含一阶导数以上的高阶分量o(u2)。在扩展卡尔曼滤波算法中用中心差分公式代替原有的对非线性函数的一阶偏导数,所得的结果将更接近于非线性函数,所以基于中心差分的扩展卡尔曼滤波算法的精度必然高于原有扩展卡尔曼滤波算法。而且,这种算法的计算量与扩展卡尔曼滤波算法的计算量相当,所以这种算法完成一次状态变量更新所用的时间与扩展卡尔曼滤波算法相近。

2.2 算法流程

中心差分扩展卡尔曼滤波算法单步流程如下:

预测状态向量:

预测协方差矩阵:

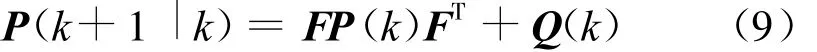
残差协方差矩阵:

应用中心差分理论得:

式中,nx表示目标运动状态向量的维数,u表示中心差分的步长。

滤波增益矩阵:

滤波输出:

滤波误差协方差矩阵:

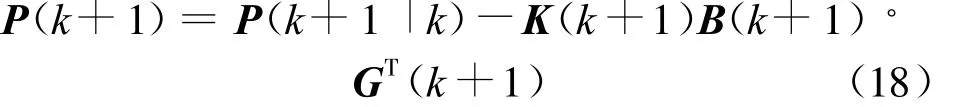
3 仿真实例

输入信号是三相交流电压信号,如图1所示,其基波频率为400 Hz,基波电压信号的幅值是115 V,5次谐波的幅值为12 V,7次谐波的幅值为10 V,11次谐波的幅值为5 V,采样时间为1 s,采样周期为10μs。该输入信号的频谱如图2所示。

图1 供电系统三相畸变电压信号Fig.1 The phase distortion signal of the power

图2 供电系统三相畸变电压频谱Fig.2 The phase distortion spectrum of the power

选取的状态方程和测量方程分别为:

式中,X(k)表示状态向量,取

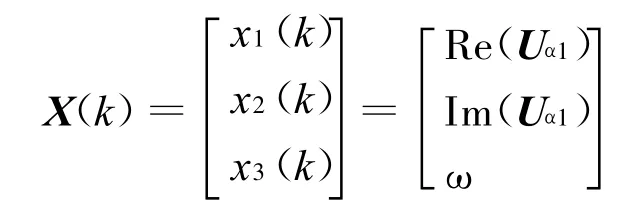
当 ω不变时,状态向量X(k)为线性函数。h(◦)表示非线性映射函数[9]。

Z(k)=h(k,X(k))表示测量向量,当ω不变时,测量向量Z(k)为非线性函数。

W(k)为状态噪声矩阵。V(k)为测量噪声矩阵。

则根据式(4),可以得到瞬态正序对称分量的曲线,如图3所示。将图3所示的供电系统电压瞬态正序对称分量信号作为EKF、UKF和CDEKF滤波算法的输入,得到通过3种滤波算法滤波后输入信号基频电压的估计曲线如图4-图5所示。

图3 供电系统电压瞬态正序对称分量Fig.3 Transient positive sequence symmetrical component of the power

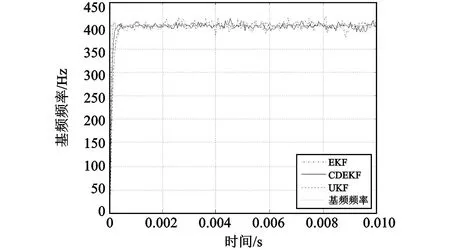
图4 3种滤波算法得到的基频频率估计曲线Fig.4 The frequency estimation curve of three kinds of filtering algorithms

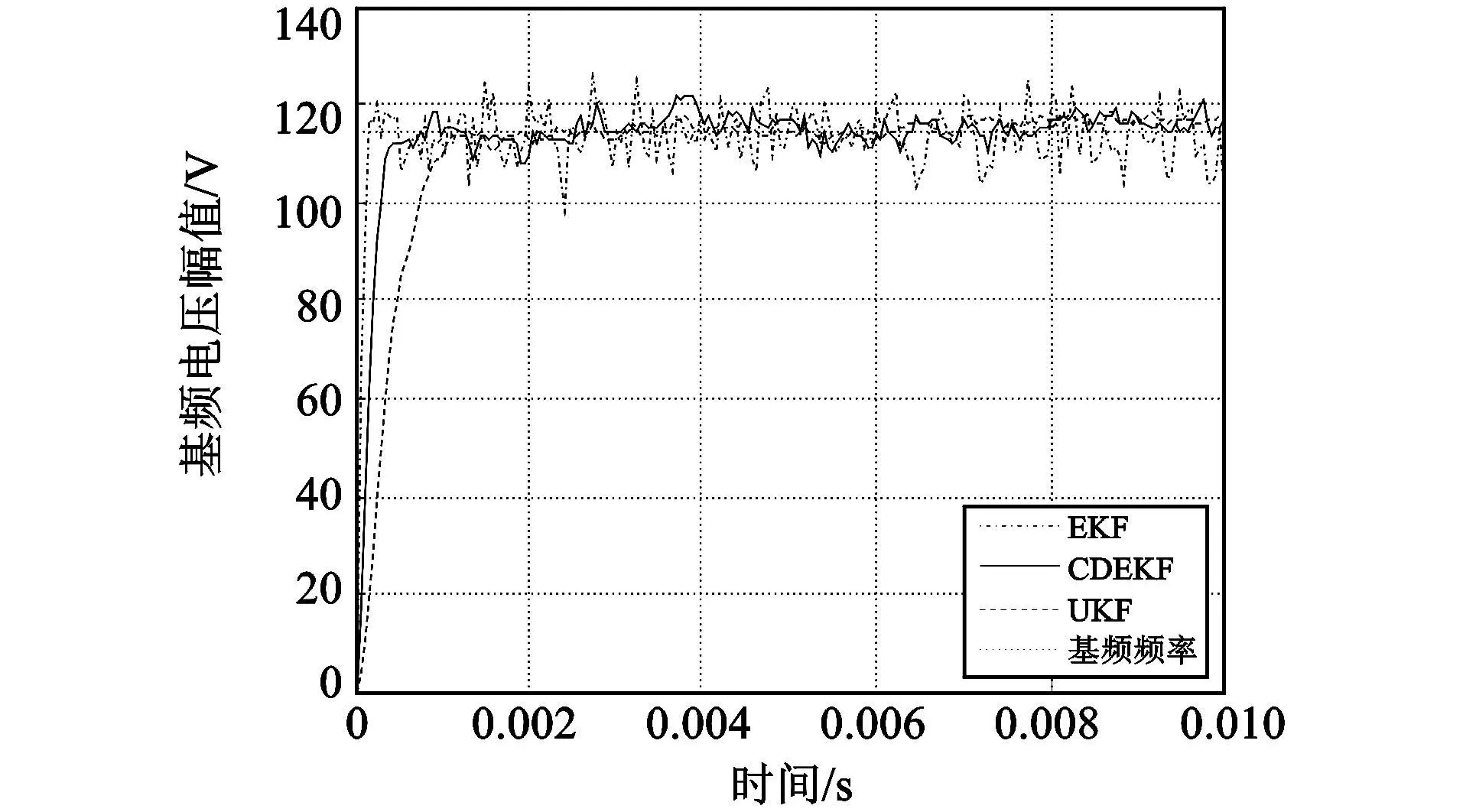
图5 3种滤波算法得到的基频电压估计曲线Fig.5 The fundamental frequency voltage curve of three kinds of filtering algorithm

表1给出了3种滤波算法经过100次蒙特卡罗仿真后得到的输入信号基频电压估计的均方根误差(RMSE)和运算时间。其中,t表示运行100次蒙特卡罗仿真的时间,t′表示在一次完整的仿真中,每完成一次状态向量更新所使用的时间。

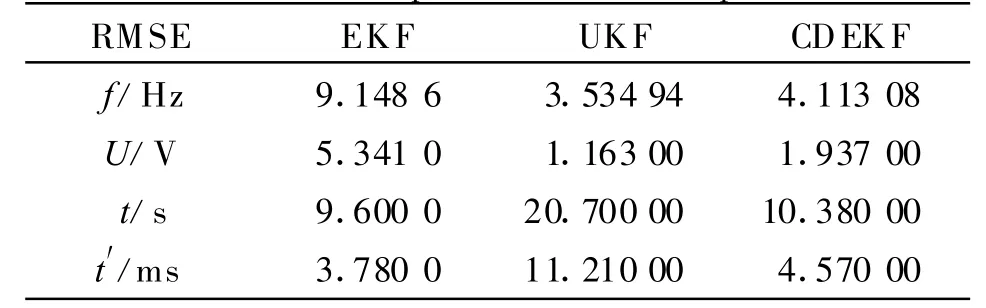
表1 EKF、UKF和CDEKF的均方根误差及运算时间比较Tab.1 EKF,UKF and CDEKF the root mean square error and computational time compared

4 结论

本文采用中心差分方法计算扩展卡尔曼滤波算法中非线性函数的一阶导数,形成了中心差分扩展卡尔曼滤波算法。理论分析和仿真表明:CDEKF与EKF和UKF相比较,虽计算时间比EKF稍有增加,但比UKF的计算时间少;而计算精度比EKF有显著提高,与UKF的计算精度相当。因此,将CDEKF应用于飞机供电系统电压信号的频率估计即可保证估计精度的要求又能缩短算法运算的时间。

[1]Logothetis A,Evans R J,Sciacca L J.Bearings-Only Tracking Using Hidden M arkov Models[J].Proceedings of the 33rd Conference on Decision and Control,1998(4):3 301-3 302.

[2]Rao S K.Pseudo-linear estimator for bearings-only passive target tracking[J].IEE Proc Radnt.Sonar Navig,2001,148(1):16-22.

[3]Julier S J,Uhlmann J K,Durrant-Whyte H E.A new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEE Transactions Automatic Control,2000,45(3):477-482.

[4]Arindam Ghosh,Avinash Joshi.A new approach to load balancing and power factor correction in power distribution system[J].IEEE Transactions on Power Delivery,2000,15(1):417-421.

[5]John S Hsu.Instantaneous phaseor method for obtaining instantaneous balanced fundamental components for power quality control and continuous diagnostics[J].IEEE Transactions on Power Delivery,1998,13(4):1 494-1 500.

[6]Gerardus C Paap.Symmetrical components in the time domain and their application to power network calculations[J].IEEE Transactions on Power Systems,2000,15(2):522-528.

[7]陆金甫,关治.偏微分方程数值解法[M].北京:清华大学出版社,2004.

[8]巫春玲,韩崇昭.用于弹道目标跟踪的有限差分扩展卡尔曼滤波算法[J].西安交通大学学报,2008,42(2):143-146.WU Chunling,HAN Chongzhao.Finite-difference extended Kalman Filtering algorithm for ballistic target tracking[J].Journal of Xi'an Jiao Tong University,2008,42(2):143-146.

[9]CUI Bowen.Positive Sequence and Frequency Estimation of Distorted Power Signals Using Extended Kalman Filter[J].Electrical Applications,2005,24(10):83-86.