摩擦耗能型TMD可行性研究

张文 裴星洙 汤曼

结构的振动控制是目前建筑结构研究的热点之一,调谐质量阻尼器(Tuned Mass Damper,TMD)是应用比较早的一种结构被动减震控制系统。正在研究中的主动控制质量阻尼器(AMD)就是由TMD系统发展而来的。主动控制系统具有体系复杂、技术要求高、价格昂贵等特点,目前主动控制方法只应用在少量超高层建筑上,且多用于结构抗风振作用。本文研究新型摩擦耗能被动控制系统,并通过模型试验验证系统减振效果,希望能将这种被动控制系统应用于结构抗震。

1 TMD的参数优化

1.1 TMD工作原理

在发生地震时,地震动将能量输入于结构,引起结构的振动反应。被动调谐质量减震控制系统,是由主体结构和附加在主体结构上的子结构构成。子结构由质量、刚度和阻尼组成,选取不同的质量、刚度和阻尼的大小,可以调节子结构振动频率。当主体结构受激励而发生振动时,子结构就能够产生一个与主体结构振动方向相反的惯性力,并作用于主体结构,减弱并控制主体结构的振动反应。当合理选择子结构各参数时,这种减震体系可以衰减主体结构地震反应的30%～60%[1]。

1.2 无阻尼结构的TMD参数优化

计算模型如图1所示。

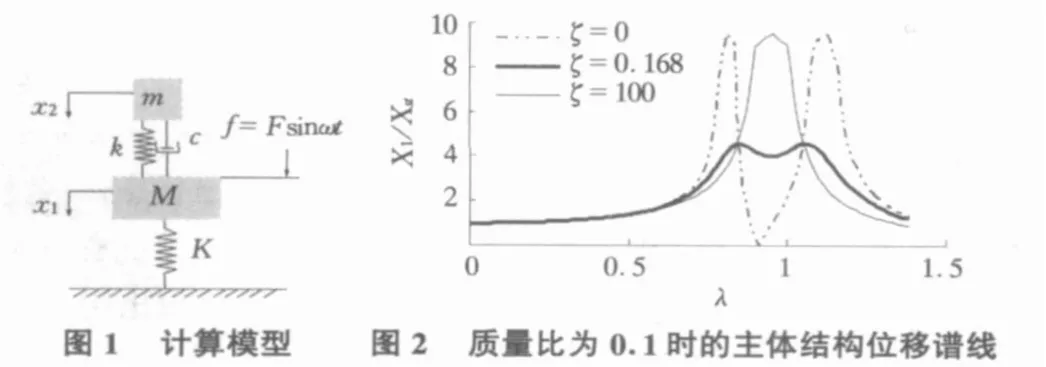
振动方程为:

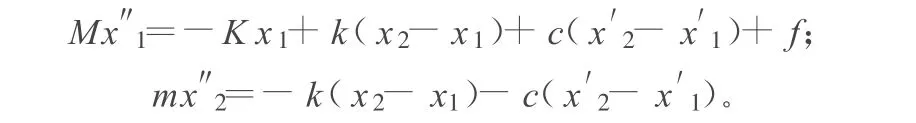
主体结构和子结构的最大位移响应分别表示为X1,X2,其表达式如下:

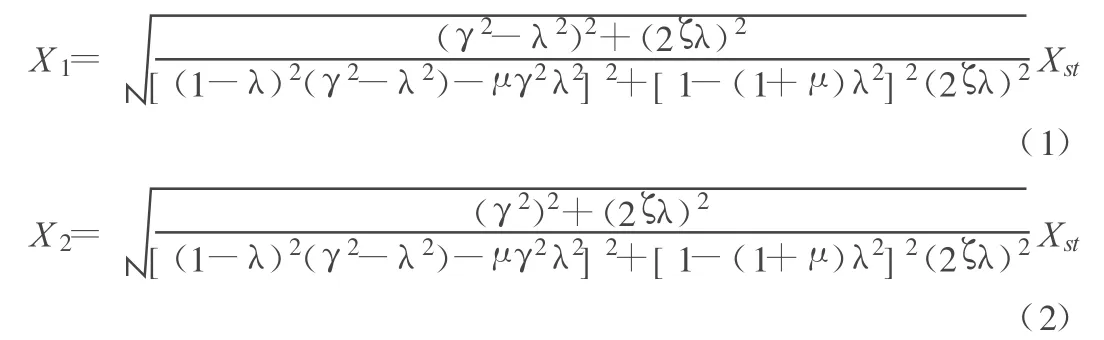
其中,μ为质量比,μ=m/M;Ωn为主体结构固有频率,Ωn为子结构固有频率,为子结构阻尼比,ζ=c/(2mΩn);Xst为主体结构最大静力作用位移,Xst=F/K;λ为激励频率与主体固有频率比,λ=ω/Ωn;γ为子结构固有频率与主体固有频率比,γ=ωn/Ωn。

以主体结构振动反应衰减最大为目标,得出以质量比为基本参数的三要素优化设计参数如下[2]:

1)子结构质量:

2)子结构弹簧劲度系数:

3)子结构阻尼:

子结构与主体结构的质量比越大,TMD的减振效果会越好,但是实际工程中质量比不可能取的过大,通常取μ≤0.2。如果取质量比为 μ=0.1做结构分析,得到如图2所示的减振效果曲线。

图2中横轴表示激励频率与主体结构固有频率的比值,纵轴表示主体结构位移峰值的放大倍数。ζ表示子结构阻尼比,质量比为0.1时,ζ的优化值为0.168,此时结构振动最大位移值可以降到最小。

2 摩擦阻尼的等效计算

以摩擦板代替粘滞阻尼器,由受摩擦力作用的自由振动衰减曲线近似计算阻尼系数,其计算模型可简化成如图3所示的模型,振动方程为:

在第一个半周期内,即0≤ωnt≤π,位移表达式为:

第二个半周期内(π≤ωnt≤2π)的位移表达式为:

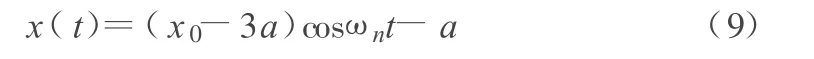
式(8)和式(9)已经能表达物体振动第一个周期内的运动。

同理可求得第二个周期内的运动方程:

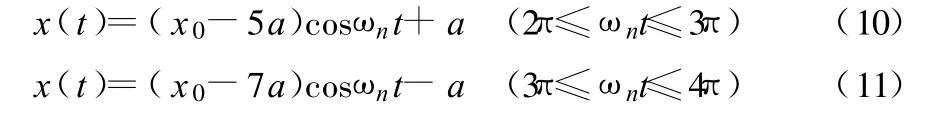
由以上方程可看出,物体运动振幅每个周期都衰减4a,因此能得到以下关系式:

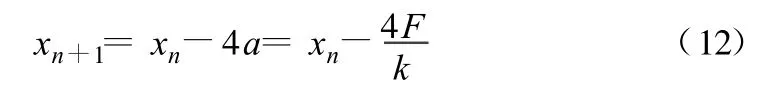
其中,xn为第n个周期的振幅;a为弹簧的弹力和摩擦力平衡时的位移量[2],a=F/k,当最大恢复力小于摩擦力时,即-a＜x＜a时,振动停止。振动曲线如图4所示。

从图4衰减曲线可以看出,摩擦阻尼力作用下的自由振动振幅为线性衰减。当最大位移量小于a时,振动即停止。以摩擦力为阻尼力的自由衰减振动曲线与粘滞阻尼器作用时的振动衰减曲线类似,同样反应振动衰减情况。当a值较大时,可以用计算粘性阻尼系数的对数衰减计算公式计算摩擦力作用下的等效阻尼系数。

取A0=X2。X2为图1中子结构的最大位移响应。以 n个周期的振幅衰减计算等效阻尼比。

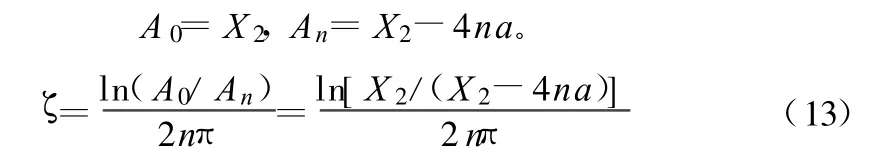
用式(13)即可近似计算摩擦力作用下的等效阻尼比。要保证公式的精确度,计算周期应该尽量多,即n应该尽可能取大值,但同时应保证 An＞0。

3 模型试验

3.1 模型基本参数

用不锈钢材料制作单质点的主体结构模型,其质量 M=5.0 kg,侧移刚度K=1 739 N/m;子结构的质量 m=0.5 kg,则体系质量比 μ=0.1。

由式(4)确定子结构弹簧劲度系数:

由式(5)可得阻尼比优化值为:

模型参数优化后最大位移谱线如图5所示。

图5中X1为主体结构位移,X2为子结构位移。从谱线可以看出,振动控制只在一些频率下有效果,在某些频率作用下甚至会加大结构振动。

为了能让模型演示减振效果,本实验选择以下参数:

M=5.0 kg,K=1 739 N/m,k=140 N/m,m=1.0 kg,ζ=0.2。

模型位移反应谱线如图6所示。

人为调节部分参数,放弃一部分优化值,这样就能够在现有的设备上演示结构的减振效果。

3.2 实验结果

分别测试一次激励和简谐激励的振动加速度曲线,将子结构作用和不作用时的结构振动加速度曲线放在同一坐标系下作对比分析,得到的结果如图7所示。

实验表明,利用摩擦滑板耗能的减振系统具有较好的减振效果。一次激励下,振动衰减明显加快。简谐激励下,可演示范围内实测模型主体结构振动减弱最大达到34.7%。

4 结语

结构振动控制将是未来建筑抗震设计的重点之一。主动控制体系的造价昂贵,由于现实技术问题,其工作状态稳定性得不到有效保证,结构被动控制具有良好的应用前景。现有的理论研究已经证实在结构顶部设置被动调谐减震控制系统(TMD)确实有一定的减振效果。通过理论分析和模型演示结果,得出用摩擦阻尼器代替粘滞阻尼器同样能够吸收振动能量,达到消能减震目的的结论。

[1]张 敏.建筑结构抗震分析与减震控制[M].成都:西南交通大学出版社,2007:188-189.

[2]背户一登,丸山晃市.振动工学[M].东京:森北出版株式会社,2002:187-192.

[3]龙驭球,包世华.结构力学[M].北京:高等教育出版社,2006:452-455.