GRAP和FUZZY集成城市轨道交通线网环境影响评价
王俊冬 陈建春
近年来,我国城市轨道交通迅速发展,“绿色交通”的理念已经在规划阶段被广泛引入。建设一种适应人居环境发展趋势的“绿色”城市轨道交通系统对于大中型城市而言尤为重要。现有的城市轨道交通线网规划可行性研究报告和环境影响评价报告对环境因素的评价大多是对已实施方案或者规划阶段的推荐方案的环境影响进行评价,这在一定程度上忽视了环境因素在方案比选阶段的指导作用,弱化了城市轨道交通设施与环境保护的协调性。另一方面,城市轨道交通线网环境影响是一个灰色系统的问题,在对其进行评价时若仅采用单一的评价方法,往往会更多的受到人为因素的影响,在一定程度上降低了整个评价的可靠性[1,2]。本文将采用GRAP和FUZZY集成的综合评价方法对城市轨道交通线网不同方案的环境影响进行评价,优选出环境合理的方案。
1 基于GRAP和FUZZY集成的综合评价方法
在模糊综合评价中引入灰色关联分析的方法,将被评判事物的数据序列作为母序列,将其影响因素的数据序列作为子序列,计算各子序列与母序列的关联度,作为系统内各因素之间关联性计量的测度,其值愈大,表明相应的子序列与母序列的关系愈紧密,因此这种关联度在基本意义上与权重是相通的,可以对其做一定的处理来代替模糊评价中的权重,这样既避免了定权过程中的主观因素影响,又能很好的解决系统中的模糊性问题。
1.1 评价指标的无量纲化处理
本文采用极差规格化法对决策矩阵进行规范化,将其变换到区间[0,1]上,最优值为 1,最差值为0。记第 t个方案的第i项指标为yti,第 i项指标的最大值为ymaxi,最小值为ymini,规范化后的指标值为eti[4]。
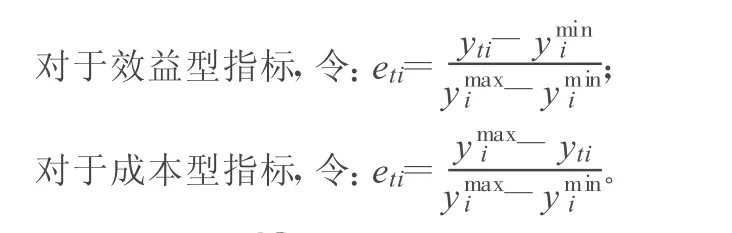
对于定性指标[5],可以采用将指标进行分等级后让专家评定的专家咨询法(Delphi法),也可以采用专家咨询法与集值统计法相结合的方法进行定量。
1.2 基于灰色关联度的权重确定[3]
1.2.1 母序列与子序列的选定
按照各个评价因素的最优值选定一个理想方案作为母序列,记为{(0)},t=1,2,…,n。待评价的各个方案为子序列,考虑有 m个子因素(已经经过无量纲化的处理),记为(i)},t=1,2,…,n。
1.2.2 计算子序列与母序列之间的关联度
计算出各子因素与母因素之间的绝对差值及其极值:
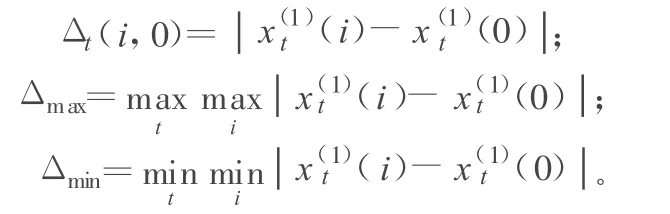
其中,i=1,2,…,m;t=1,2,…,n。利用下式计算出各子序列与母序列之间的关联度:
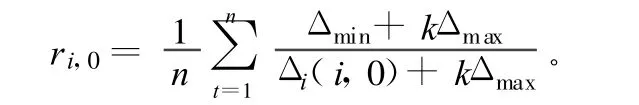
其中,i=1,2,…,m;k∈(0.1,1),一般取0.5。由此可见,关联度是一个有界的数值,其取值范围在0.1~1之间,愈接近于1表明子因素对主因素的影响愈大,反之亦然。
1.2.3 由关联度向权重的转换
1.3 确定模糊关系矩阵,进行模糊综合评判
1)确定评语集。对各因素的无量纲化指标值的区间进行模糊语言变量划分 V={v1,v2,…,vl},模糊划分的语言变量个数决定了最大可能的规则个数。
2)进行单因素评判,得到单因素评判集 R。对各个语言变量建立各自的模糊隶属度函数,分别对评判对象的全体因素计算隶属度函数值rml,由此构成单因素评判集合R,即一个评价对象的模糊关系矩阵R。其中隶属度值的确定在模糊综合评价中非常关键,确定隶属度值通常采用的是专家咨询法或主观评测法,但这两种方法都不可避免的会给整个评价结果带来人为色彩,在一定程度上影响了评价的精度。本文将对0~1的区间上划分为5个变量,构成评语集:V={很差,差,一般,好,很好},采用三角形隶属度函数,计算出每个方案各个指标值隶属于模糊语言变量的程度。
3)进行模糊合成,做出决策。选择合适的模糊算子,将各方案的模糊关系矩阵R与指标权重集A合成得到各被评对象的模糊综合评价结果向量B,即模糊综合评价向量B=A⊗R={b1,b2,…,bl}。其中,运算“⊗”在因素个数大于4个时,通常采用普通矩阵乘法运算。对得到的每一个方案的模糊综合评价向量B,均可以通过最大隶属度原则、加权平均原则或模糊向量单值化原则来确定被评方案的优劣等级,最终优选出最佳方案。
2 实例分析
本文选取文献[2]中西安市城市轨道交通线网规划的实例,并对评价指标进行适当的调整,采用基于灰色和模糊理论集成的方法进行环境影响综合评价。
2.1 各方案指标值的无量纲化处理
按照上述方法,将各个方案的指标值分别进行无量纲化处理,处理结果见表1。

表1 各方案指标值的无量纲化数值
2.2 基于灰色关联度的指标权重确定
由上述无量纲化数据,理想方案的指标集取:

由此得到关联度矩阵为:
~ξ16×1={0.510 0.524 0.628 0.74 0.671 0.538 0.703 0.5 0.525 0.647 0.68 0.708 0.706 0.535 0.645 0.645},对关联度矩阵进行归一化处理后,各因素的权重集为:
~A=[0.052 0.053 0.063 0.075 0.068 0.054 0.071 0.05 0.053 0.065 0.069 0.071 0.071 0.054 0.065 0.065],由上述三角形隶属度函数可以得到每个方案对应的单因素隶属度矩阵R,如Ⅰ方案的隶属度矩阵为:

同理可得到另外三个方案的隶属度值矩阵。
2.3 模糊合成
选择普通矩阵的乘法为模糊算子,进行模糊矩阵的合成运算,得到各方案的模糊综合评价向量 B。如,B1=A·R(1)T={0.281 0.049 0.122 0.280 0.269},同理可得到其他方案的模糊综合评价向量,B2={0.500 0.110 0.087 0.122 0.180};B3={0.584 0.064 0.164 0.029 0.158};B4={0.158 0 0.043 0.100 0.699}。对于模糊合成的各方案的评价向量,采用模糊向量单值化处理,即给很差、差、一般、好、很好5个语言变量分别赋以分值1,2,3,4,5,组成矩阵 V={1 2 3 4 5},由综合评判值Z=B·VT,可以分别得到四个方案的综合评判值:Z1=3.207;Z2=2.371;Z3=2.114;Z4=4.182,因此方案排序的结果为:Ⅳ>Ⅰ>Ⅱ>Ⅲ。
3 结语
1)与文献[2]中采用单一灰色评价模型的计算结果相比,本文的计算结果包含的信息量更为丰富,各方案的综合评判值之间差异性更明显,更易于优选出合理方案。2)本文采用的综合评价模型在模糊综合评价中引入灰色关联度模型,指标定权时充分利用了已有的定量化数据,尽可能的降低了评价过程中的主观因素的影响,提高了整个评价结果的可靠程度。计算结果表明,这种集成模型在评价城市轨道交通线网环境影响这类同时具有灰色性和模糊性的问题时,能够充分发挥两种评价方法的优势,各取所长,且定量化程度高,计算简单,具有更强的实用性。
[1]白 雁,魏庆朝,邱青云.基于绿色交通的城市交通发展探讨[J].北京交通大学学报(社会科学版),2006,5(2):10-14.
[2]覃路燕.城市轨道交通线网规划环境影响评价指标体系应用研究[D].西安:长安大学,2009.
[3]杜 栋,庞庆华,吴 炎.现代综合评价方法与案例精选[M].北京:清华大学出版社,2008:198-203.
[4]冉茂平,吴小萍.基于灰色关联系数法的铁路建设项目社会经济环境影响评价[J].水土保持研究,2006,13(1):173-175.
[5]吴小萍,詹振炎.基于灰色和模糊集理论的铁路方案多目标综合评价方法及模型研究[J].铁道学报,2001,23(5):107-113.
[6]黄 卫,刘新旺.基于模糊推理的公路工程质量评定模型[J].系统工程理论与实践,2001(9):109-113.

