高速列车—无砟轨道—桥梁耦合系统振动特性分析

利远翔,雷晓燕,张 斌

(华东交通大学铁路环境振动与噪声教育部工程研究中心,江西南昌330013)

国内外对于车辆—轨道系统动力学及车辆—桥梁系统动力学的研究已经相当深入,但是由于各自不同的目的,将车辆、轨道和桥梁作为一个整体系统加以研究的却不多见。从上世纪80年代起,国内外学者对快速列车和重载列车引起的地面振动及对周围环境的影响进行了较多研究,提出了一些计算方法和计算模型。如在1994年,日本的Fujikake[1]和松浦章夫[2]分别就交通车辆引起的结构振动发生机理、振动波在地下和地面的传播规律及其对周围居民的影响进行了研究,提出了环境振动水平的预测方法。日本铁道技术研究所还就新干线高速列车对环境振动的影响进行了现场测试,分析了车辆、轨道、桥梁等不同部位的振动特点,并研究了不同类型屏障的隔振效果。而对于高架轨道系统诱发环境振动特性的研究,源自于1999年开始动工修建的台湾高速铁路,经过台南高科技园区的一段高架轨道振动超标,从而引起了国内外学者对高架轨道诱发环境振动的关注并开始研究。台湾成功大学教授朱圣浩等[3-4]采用有限元的方法,在建立车辆—桥梁—大地耦合振动的三维有限元模型时,将列车以动轮单元模拟,大地采用三维块体单元模拟,分析了高架轨道引起的周边建筑物的振动。本文建立了车辆单元模型、轨道—桥梁单元模型,推导了车辆—轨道—桥梁耦合系统的振动方程,并在Matlab软件中编制了程序,最后通过一个实例分析了高速列车—无砟轨道—桥梁耦合系统垂向振动特性。

1 车辆单元模型

本文的模型是在雷晓燕教授的车辆—轨道—地基耦合系统模型[5-7]的基础上建立的。图1为车辆单元模型,在整车模型中,车体和转向架考虑沉浮振动和点头振动,车轮考虑沉浮振动,每节钢轨上两个节点考虑竖向位移和转角,整车模型有26个自由度。

图1中,Mc,Jc为车体的质量与转动惯量;Mt,Jt为转向架的质量与转动惯量;ks1,ks2为车辆一、二系悬挂刚度;cs1,cs2为车辆一、二系悬挂阻尼;Mwi(i=1,2,3,4)表示第 i个车轮的质量;kc为轮轨间接触刚度;vc,θc为车体沉浮振动的竖向位移、车体点头振动的角位移;vi,θi(i=t1,t2)表示前、后转向架沉浮振动的竖向位移、点头振动的角位移;vi(i=w1,w2,w3,w4)为第i个车轮的竖向位移;vci(i=1,2,3,4)为第i个轮轨接触处钢轨的竖向位移。

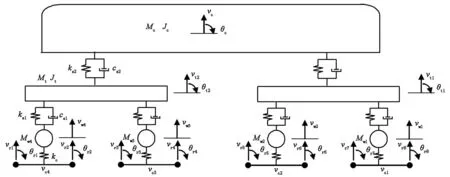
图1 车辆单元模型

从图1中我们可以定义车辆单元的节点位移向量为

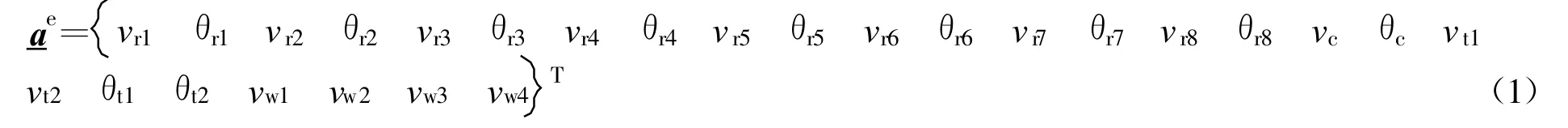
为了建立车辆单元的有限元方程,可以运用Hamilton原理,即

其中:L为Lagrange函数,L=T-Π;T为动能;Π为势能;R为耗散能。

通过列出车辆单元的弹性势能、动能和耗散能可推导出车辆单元的刚度矩阵、质量矩阵和阻尼矩阵

2 轨道—桥梁单元模型

四层轨道—桥梁单元模型如图2所示,将轨道结构和桥梁简化为四层梁模型,从上到下分别为钢轨、轨道板、混凝土支承层和桥梁。模型仅考虑沉浮和点头振动,共有16个自由度。图2中v1,v5表示钢轨的竖向位移;θ1,θ5表示钢轨的转角;轨下垫层的支承弹性系数和阻尼系数分别用ksy1和csy1表示;v2,v6表示轨道板的竖向位移;θ2,θ6表示预制轨道板的转角;轨道板下沥青水泥砂浆层的支承弹性系数和阻尼系数分别用ksy2和csy2表示;v3,v7表示混凝土板支承层的竖向位移;θ3,θ7表示混凝土板支承层的转角;底座混凝土板支承层下桥梁的支承弹性系数和阻尼系数分别用ksy3和csy3表示;ν4,ν8表示桥梁单元的竖向位移;θ4,θ8表示桥梁单元的转角。

从图2中我们可以定义轨道—桥梁单元的节点位移向量为

同样为了建立轨道—桥梁单元的有限元方程,利用Hamilton原理,通过列出轨道—桥梁单元的弹性势能、动能和耗散能可推导轨道—桥梁单元的刚度矩阵e、质量矩阵e和阻尼矩阵e。

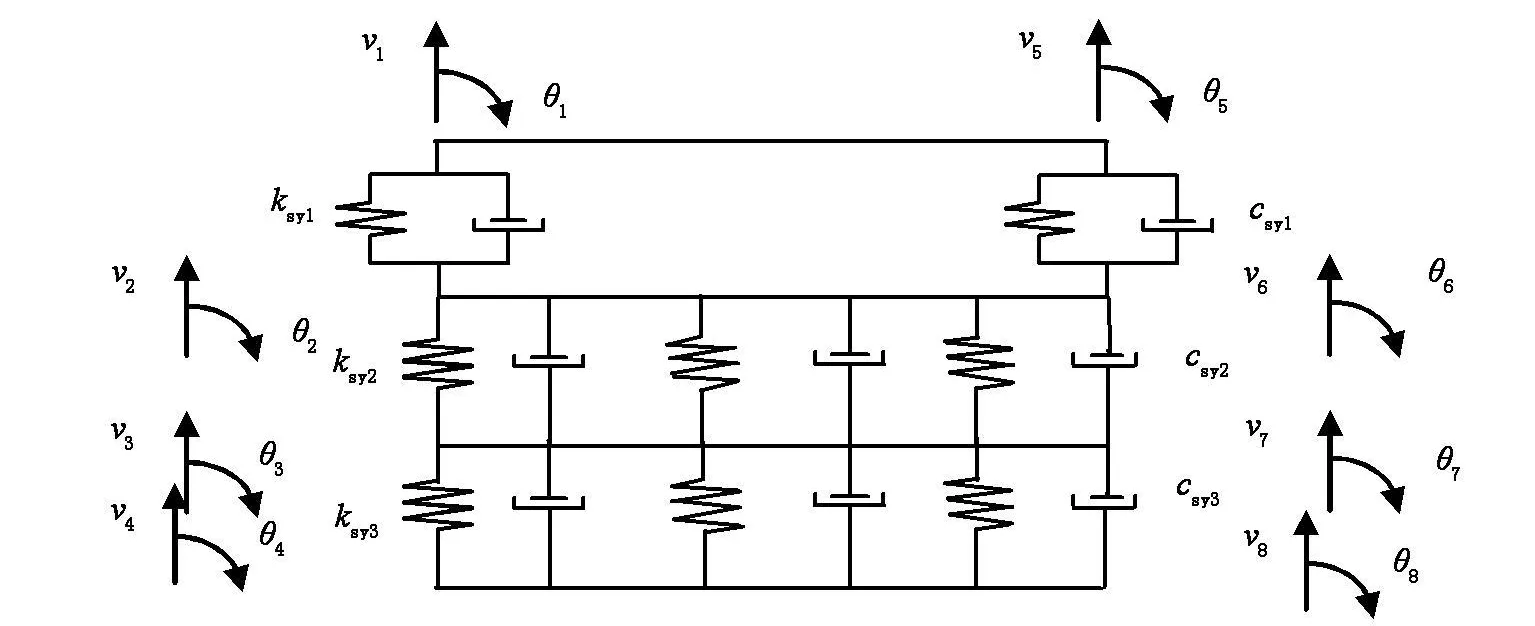
图2 板式轨道—桥梁单元模型

2.1 轨道—桥梁单元的弹性势能

轨道单元的势能包括钢轨的弯曲势能,预制轨道板的弯曲势能,底座混凝土板支承层的弯曲势能,桥梁的弯曲势能,离散支承弹簧的势能以及连续支承弹簧的势能。

(1)钢轨的弯曲势能

钢轨上任意一点的位移可表示为

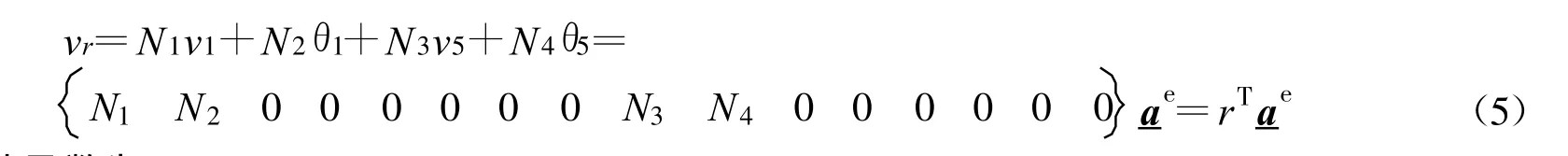
其中位移插值函数为

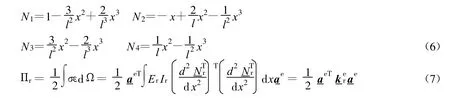
其中

2.2 轨道—桥梁单元的动能

轨道单元的动能包括钢轨的弯曲动能,预制轨道板的弯曲动能,底座混凝土板支承层的弯曲动能以及桥梁单元的弯曲动能。

(1)钢轨的弯曲动能

其中

同理可以推导出预制轨道板单元的质量矩阵、底座混凝土板支承层单元的质量矩阵和桥梁单元的质量矩阵

2.3 轨道—桥梁单元的耗散能

(1)比例阻尼

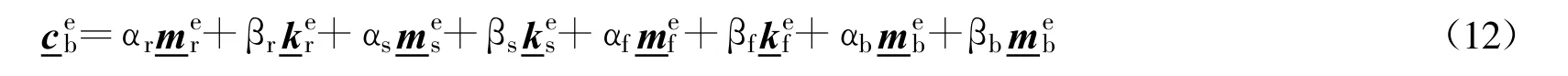
(2)离散支承弹簧的耗散能

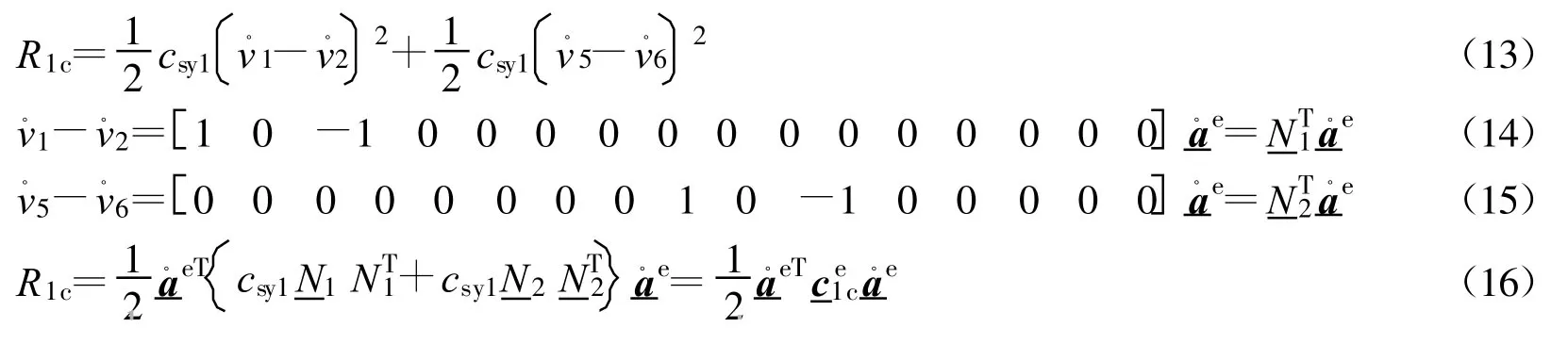
2.4 轨道—桥梁单元的运动方程

得板式轨道—桥梁单元四层梁的有限元方程如下

其中

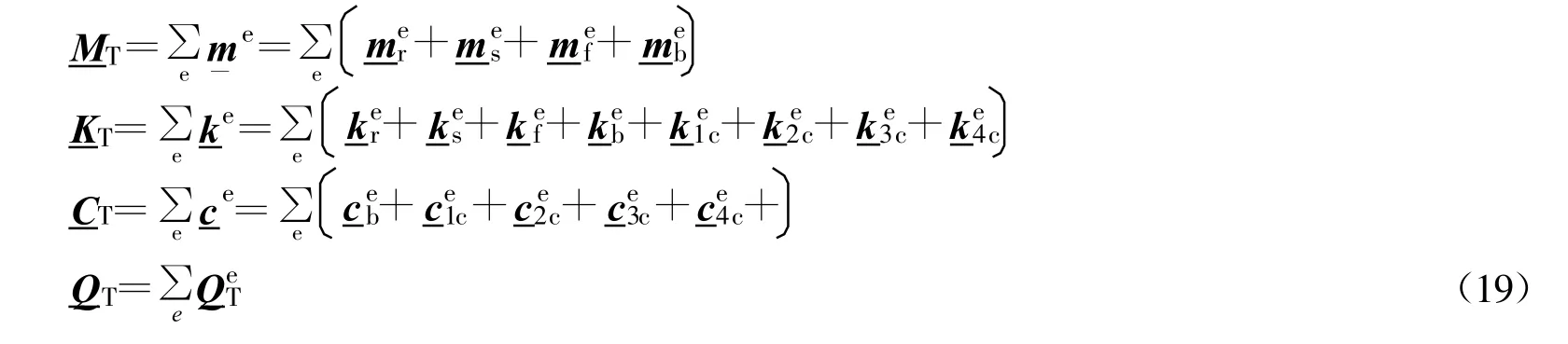
3 车辆—轨道—桥梁耦合系统有限元方程

考虑车辆—无砟轨道—桥梁耦合系统的有限元方程包含两种单元,即无砟轨道—桥梁单元和车辆单元,相应的单元刚度矩阵、质量矩阵和阻尼矩阵分别为Ku,Mu,Cu见(3)和KT,MT,CT见(19)。利用标准有限元的集成方法可形成车辆—无砟轨道—桥梁耦合系统的总刚度矩阵、总质量矩阵和总阻尼矩阵。最后得到车辆—无砟轨道—桥梁耦合系统的动力有限元方程如下:

其中

考虑桥梁支承处的边界条件,即桥墩沿竖直方向的位移为零,车辆—无砟轨道—桥梁耦合系统动力有限元方程数值解的实现,可通过直接积分法,如Newmark数值积分法。

4 车辆—轨道—桥梁耦合系统算例以及分析

对上述车辆—无砟轨道—桥梁耦合系统有限元模型运用Matlab编制了计算程序,并进行了实例计算。现利用编制的程序分析高速列车—无砟轨道—桥梁耦合系统垂向振动特性。考虑8跨连续梁的情况,桥梁跨度32 m,整个桥长256 m,列车时速300 km◦h-1,混凝土支承块间距0.65 m,时间步长0.001 s。车辆、轨道和桥梁结构的参数见表1和表2。为简化计算,不计轨道随机不平顺。

通过仿真分析可以得出轮轨接触力、钢轨竖向位移、桥梁竖向位移等时程曲线图,分别见图3～图7。

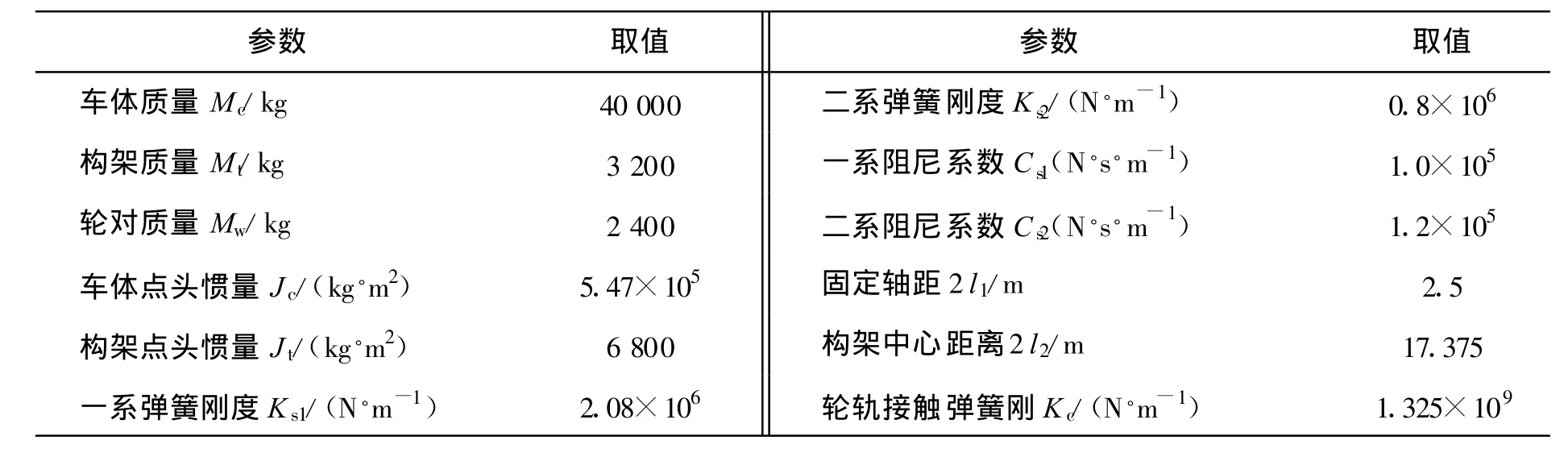
表1 和谐号高速动车CRH3车辆结构参数

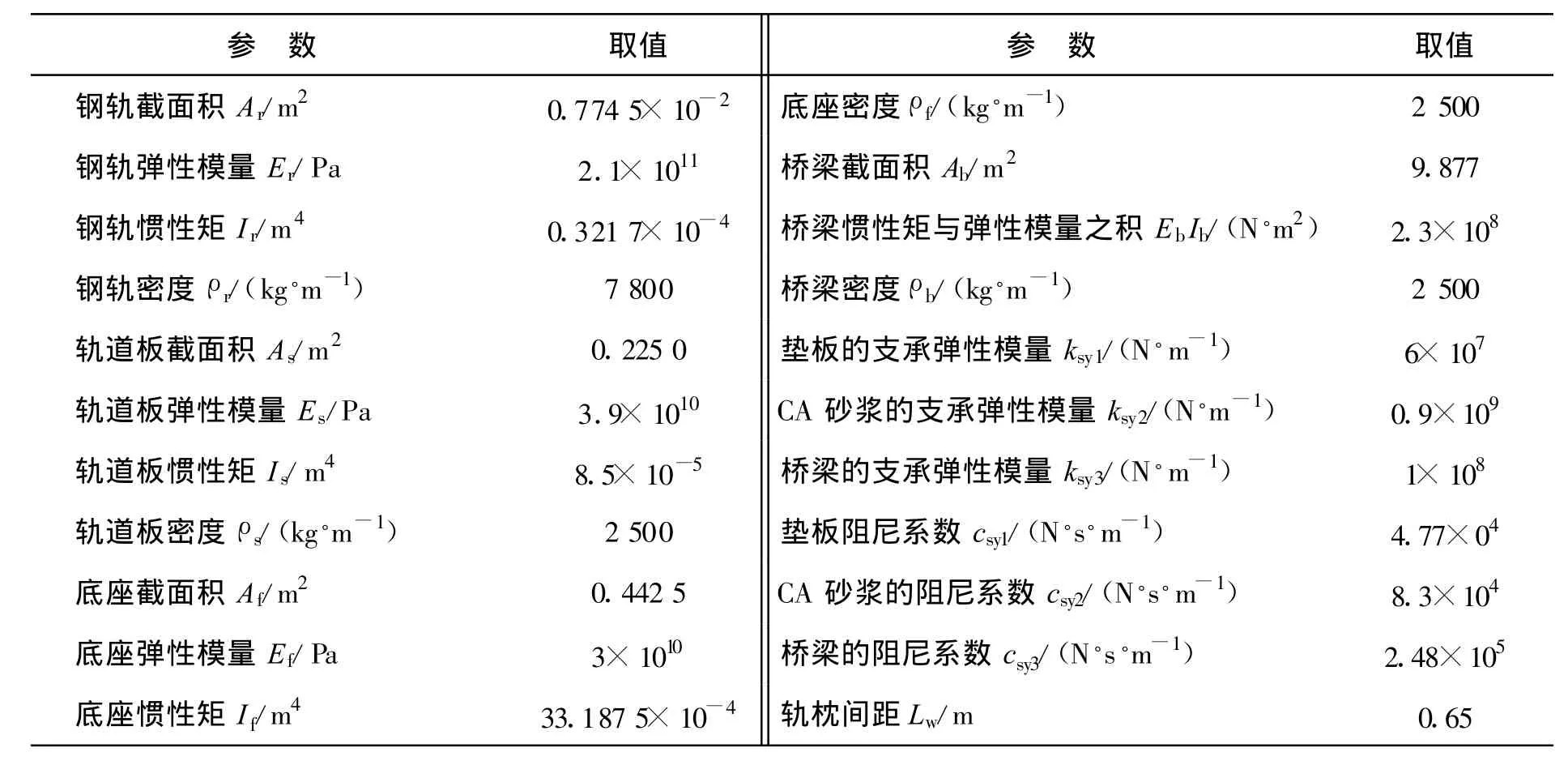
表2 CRTSⅡ型板式无砟轨道和桥梁结构参数

从时程曲线图可以看出:轮轨接触力保持在70 kN左右,从钢轨竖向位移时程曲线图中可以明显的看出四个轮对与钢轨接触时的四个峰值,而且在钢轨竖向加速度时程曲线图中也可以看出四个峰值。还可看出钢轨位移时程曲线与桥梁时程曲线图相比较,前者的振动位移比后者的大,在轨道—桥梁单元模型中的四层梁中,从上到下位移呈递减的趋势。钢轨和桥梁的振动加速度也呈现相同的规律。

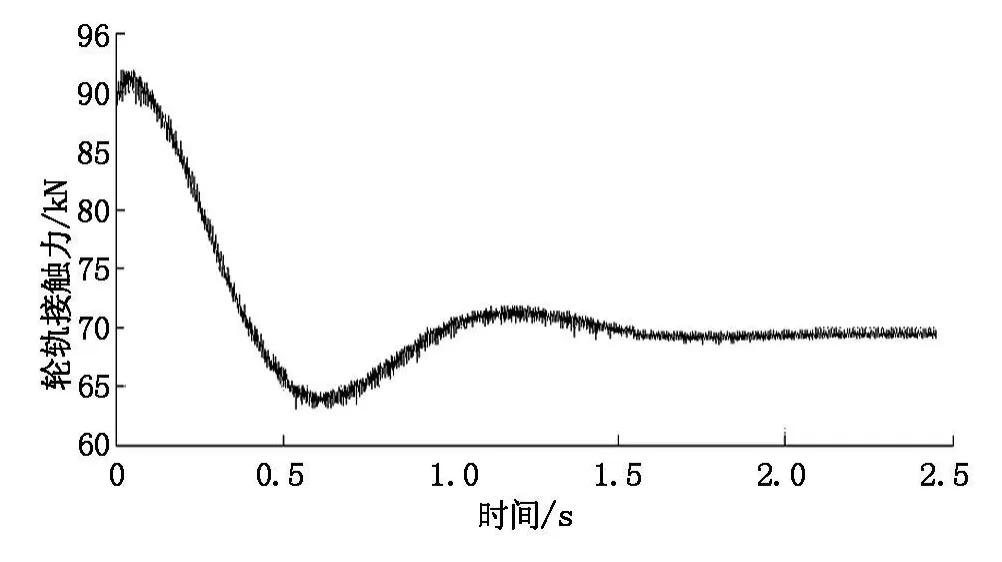
图3 轮轨接触力时程曲线

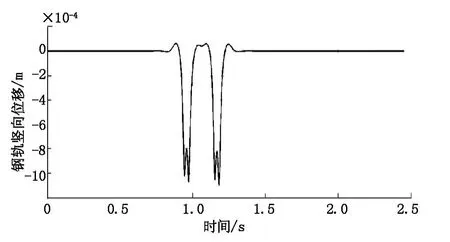
图4 钢轨竖向位移时程曲线

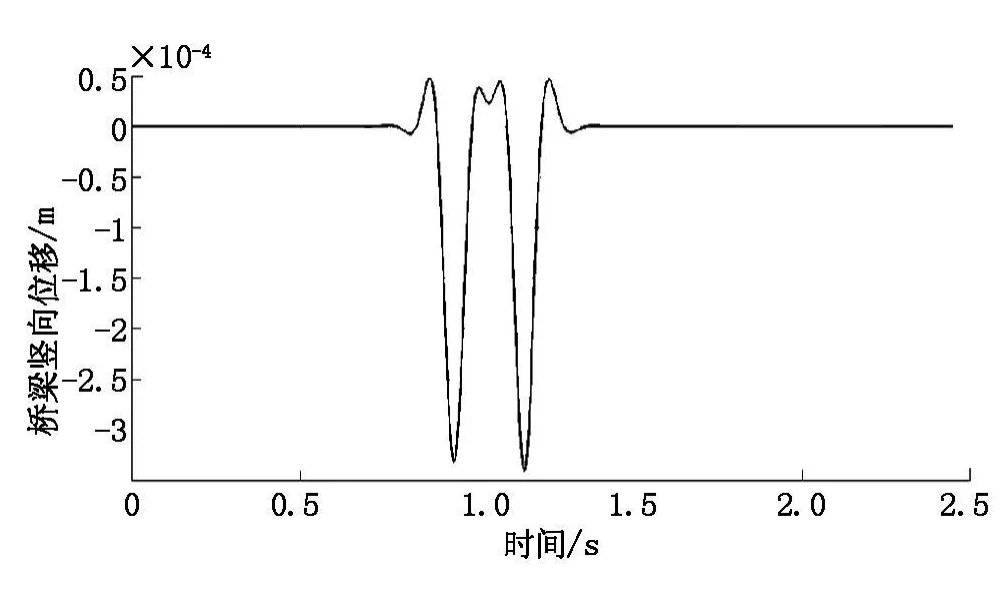
图5 桥梁竖向位移时程曲线

图6 钢轨竖向加速度时程曲线图

5 结论

通过建立车辆单元模型和轨道—桥梁四层梁单元模型,利用拉格朗日方程推导出整个耦合系统的刚度、质量和阻尼矩阵,最后得出耦合系统的振动方程。相对于其它复杂的车辆—轨道—桥梁耦合动力学模型,该方法思路清晰,借助于Matlab软件使得程序编制容易实现,计算时效快且能反映轨道—桥梁振动的基本规律和特点。

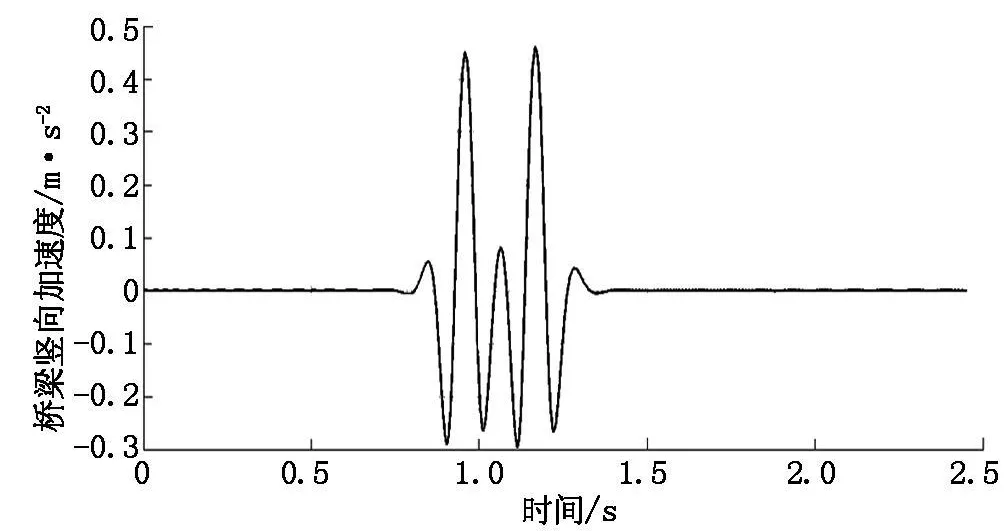
图7 桥梁竖向加速度时程曲线图

[1]FUJIKAKE T.A predictionmethod for the propagation of groundvibration from railway trains[J].Journalof Sound and Vibration,1986,111(2):357-360.

[2]松浦章夫.高速铁路车辆与桥梁相互作用[J].铁道技术研究资料,1974,31(5):14-17.

[3]JU SHENHAW,LIN HUNGTA.Analysis of train-induced vibrations and vibration reduction schemes above and below critical Rayleigh speeds by finite element method[J].Soil Dynamics and Earthquake Engineering,2004,24(4):993-1 002.

[4]JU SHENHAW,LIN HUNGTA.A simple finite element model for vibration analyses induced by moving vehicles[J].Soil Dynamics and Earthquake Engineering,2006,68(12):1 232-1 256.

[5]雷晓燕现代铁路理论研究[M].北京:中国铁道出版社,2006.

[6]雷晓燕,张斌,刘庆杰.列车—轨道系统竖向动力分析的车辆轨道单元模型[J].振动与冲击,2009,29(3):168-173.

[7]雷晓燕,张斌,刘庆杰.轨道过渡段动力特性的有限元分析[J].中国铁道科学,2009,30(5):15-21.