带有阻尼项的三维欧拉方程组球对称解

俞银晶,朱旭生,李 翠

(华东交通大学基础科学学院,江西南昌330013)

本文研究了一类带有球对称性质的等熵可压缩气体动力学的欧拉方程组,方程组形式为

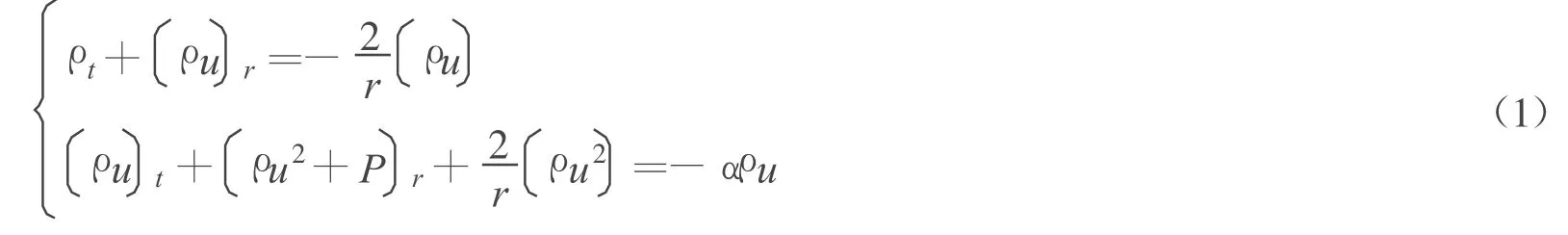
式中:标量函数ρ,u分别表示气体密度、速度;r＞0为空间变量;t＞0为时间变量;P表示气体压强,并满足P(ρ)=a2ργ;a为正常数;γ为绝热指数;-α ρ u表示阻尼项;α为常数。

对于一维欧拉方程,经典解的存在性和爆破问题已经被很多人研究过了,在文献[1]中研究了一维带阻尼项的Euler方程组初边值问题的齐次Dirichlet边值情形。当初值在平衡解附近小扰动时,得到了时间整体解的存在唯一性,在文献[2]中介绍了大初值条件下,一维欧拉方程组经典解的爆破。因此,本文考虑把三维欧拉方程转化为一维欧拉方程,即通过球对称变换,降低维数,进而简化运算,得到解的存在性。

首先,方程组(1)转化为对称双曲型方程,进而得到局部解的存在性;其次,在等温情形下,利用方程的转化和在文献[3]中提到的Lagrangean质量坐标的引入,方程组(1)被转化为p-系统。考虑到p-系统的研究成果很多,本文通过已研究的带线性阻尼项的p-系统的理论,以及文献[4]对非齐次项的考虑,得到了方程的近似解,最后,推得在有限时间区间里,近似解收敛,并证明它为一个弱解。

1 局部解存在性

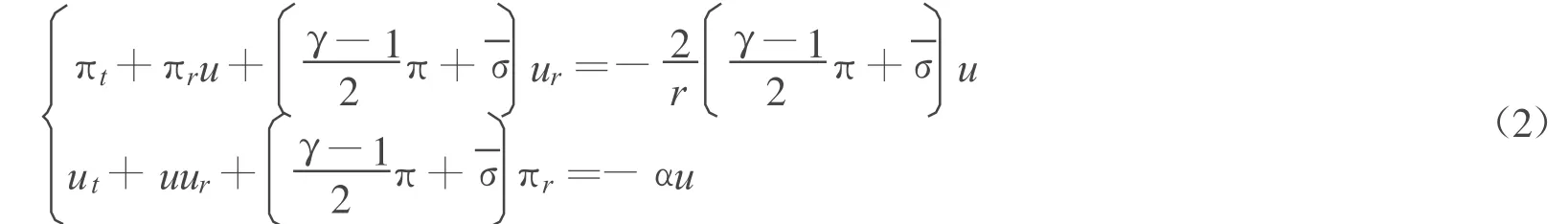
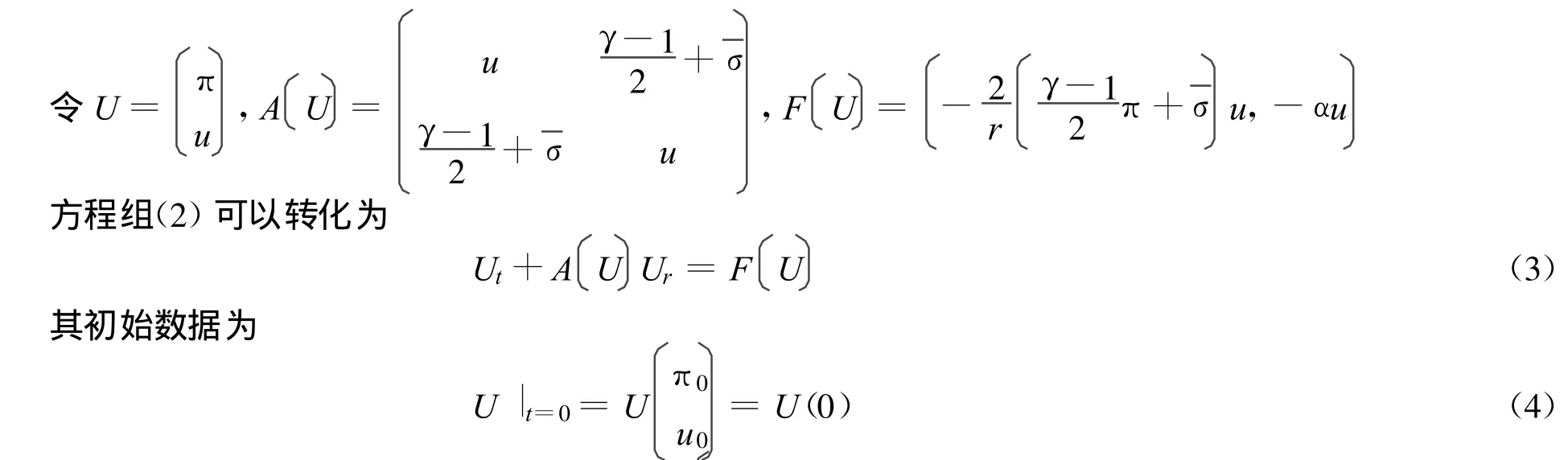
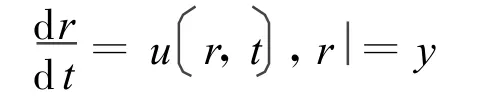
沿着粒子轨迹,对密度求导得

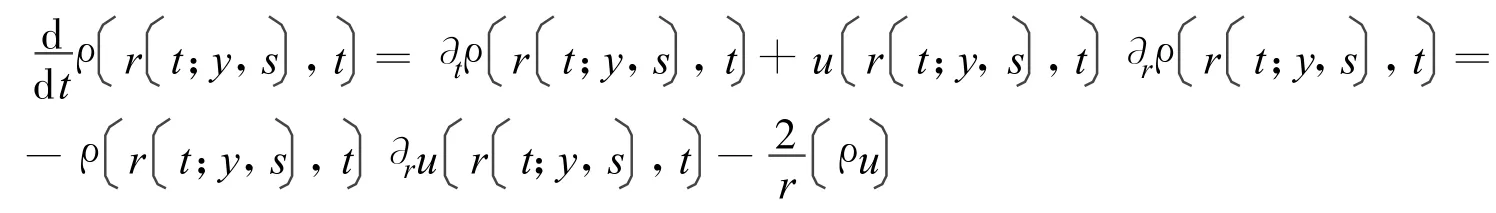
解此常微分方程得

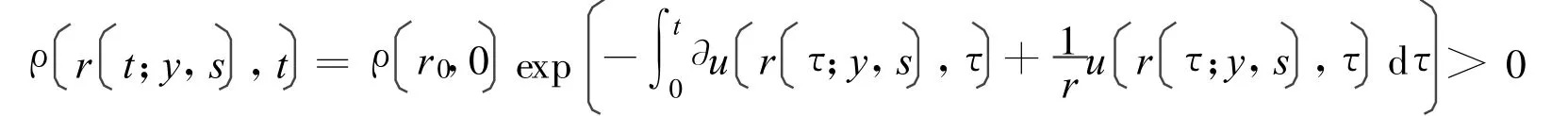
由此可见,引理成立。

由对称双曲型方程组Cauchy问题解的局部存在性理论[5],上述式子(3)(4)有关于时间的局部存在性结论。

2 弱解的存在性

已知对于三维欧拉方程组,整体解的存在性很难得到,下面证明三维等熵欧拉方程组整体弱解存在。首先,把方程组转化为p-系统。

由方程组(1)可知,在r=0处有奇异点。因此,设1≤r＜∞,也就是在单位球的外部讨论该方程的初边值问题:

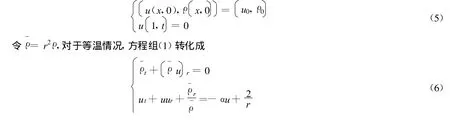
由文献[3],引入lagrangean质量坐标

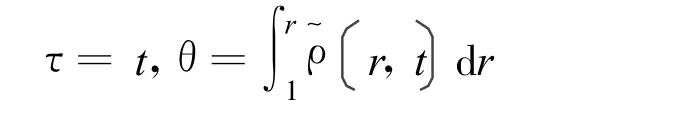
计算得

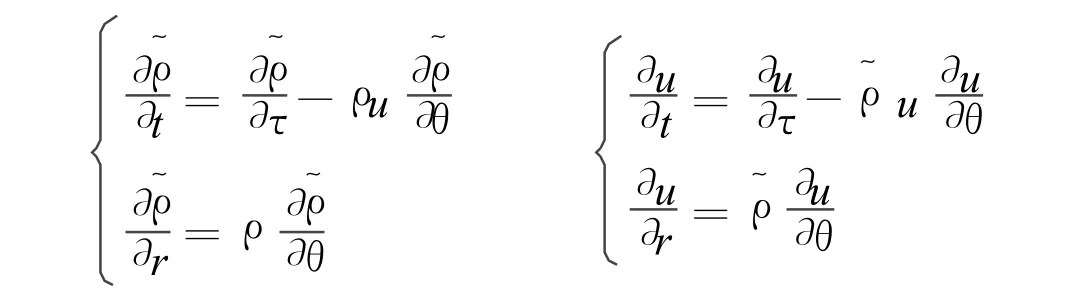
下面考虑方程组(7)的初边值问题:

证明 先给出弱解的定义。

引理3[6]如果存在,使得

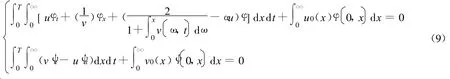
那么称u,v为式子(7)(8)的弱解。

为了证明定理2,我们利用Glimm模式[7]先建立一组近似弱解;然后由其收敛,并通过细致的验算可以得到式子(9)成立。具体过程如下:

根据文献[7]中定理5.1.3有:

4.4 对同一年份春季干旱评估，相对湿润度指数(M指数)及标准化降水指数(SPI指数)的等级划分不同，天峻地区春季“十年九旱”的实际情况，相对湿润度指数(M指数)对天峻干旱等级的评估更合理。

存在收敛于0+的数组使得对所有 m,当变量时,有

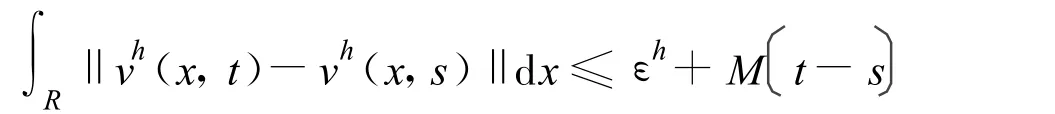
黎曼问题的中心在t=0,x=jΔx,这里j为奇数。

对于初边值问题:

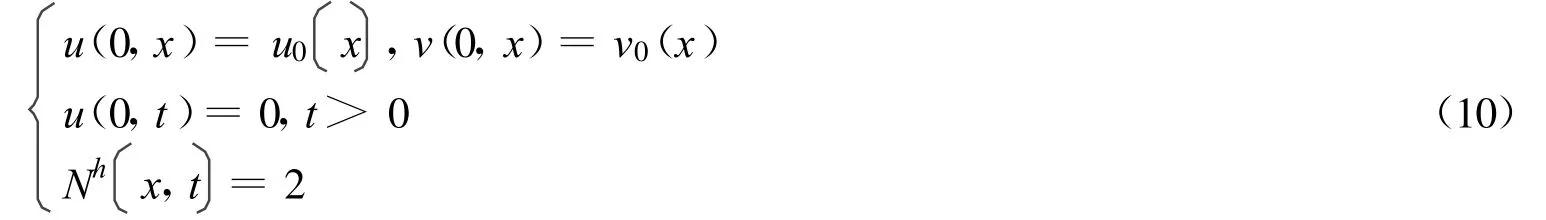
假如 uh,vh已经被定义在0＜t＜nΔt,对于nΔt≤t＜(n+1)Δt,jΔx≤x ＜(j+2)Δt,这里j为奇数。定义

这里uh0,vh0表示如下:

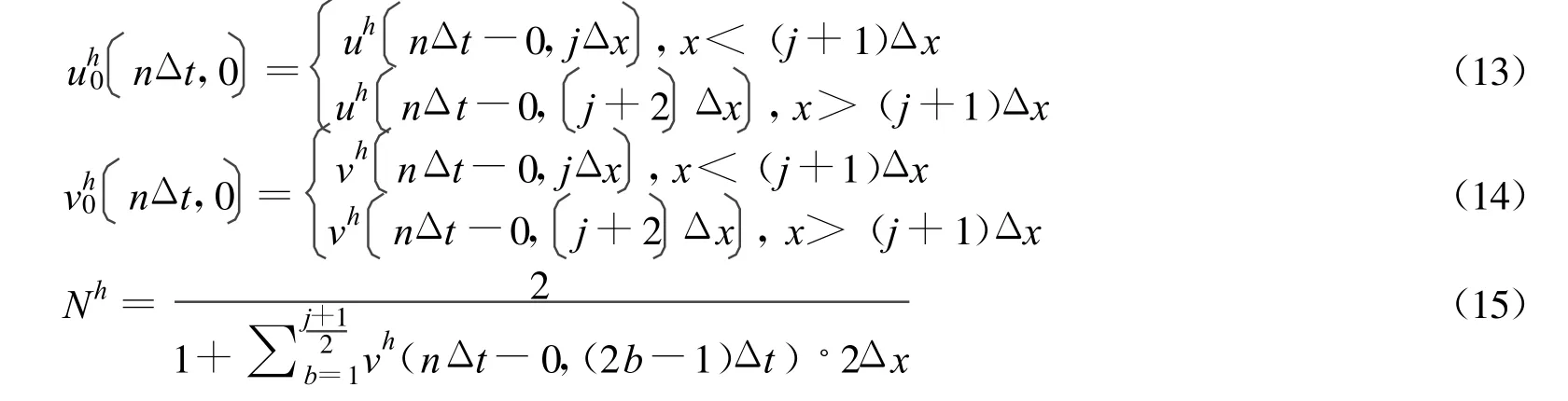
于是就得到了近似解uh,vh,再由定理的条件以及引理4,可得uh,vh有界。那么存在u,v,使得 uh,vh在局部可积空间中唯一收敛到u,v。

下面证明u,v为弱解,也就是式子(9)成立。令函数φ,ψ为对于区间{(x,t):0＜x＜∞,0＜t＜T}的紧集,并有先证方程组(9)中第一式,由于 uh为弱解,那么满足:

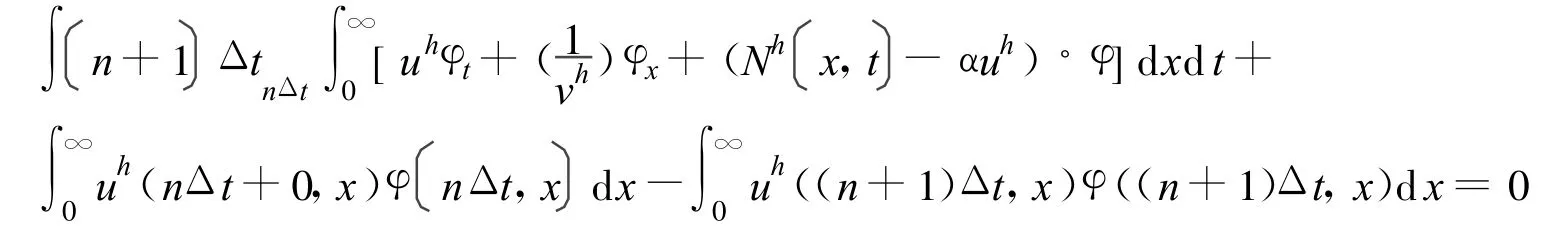
对 n求和,有

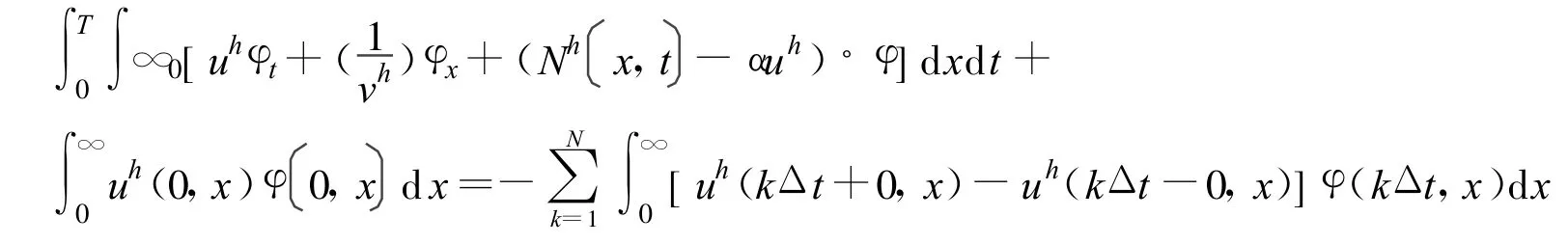
这里 N=T/Δt,当N →∞时,上述方程的右边趋向于零,左边 uh→u,vh→v,则

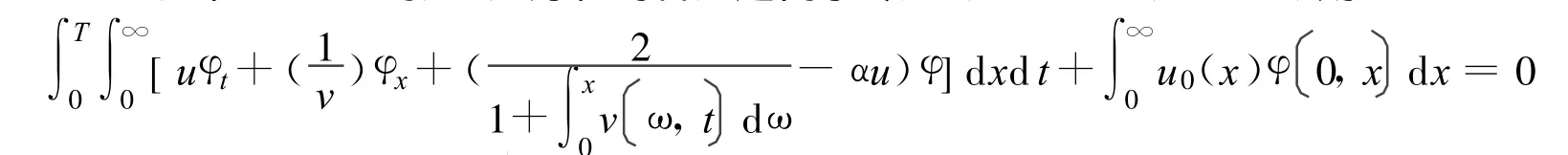
由于 vh为弱解,满足

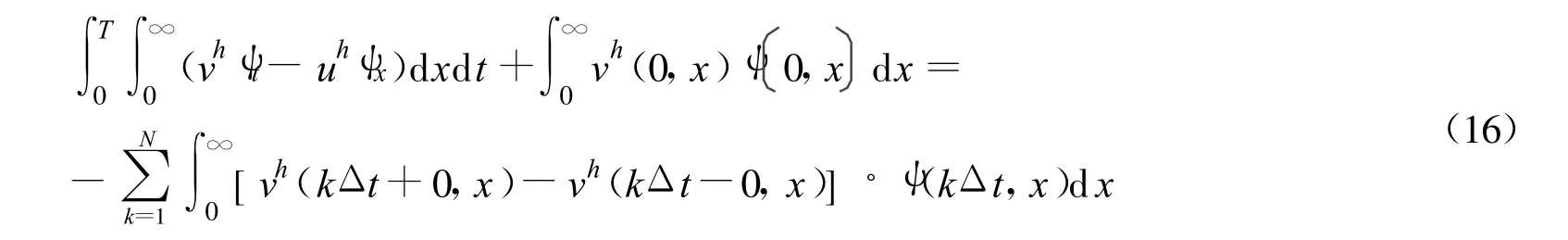
等式右边 =-I1-I2。这里

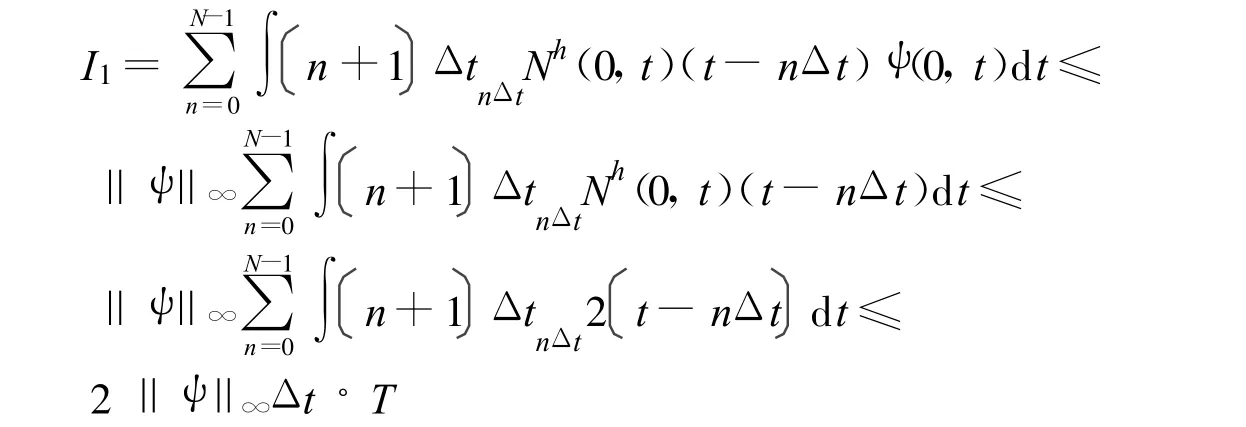
当N →∞时,Δ t→0,表示了网格分得足够细时I1→0。

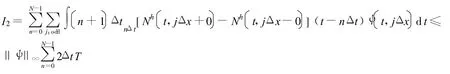
当N →∞时,Δt→0,表示了网格分得足够细时I2→0。

式子(16)左边当N→∞时,uh→u,vh→v,那么方程组(9)的第二式成立。

综上可知,定理2成立。

[1]朱旭生.带阻尼项的Euler方程组初边值问题的经典解[J].数学杂志,2004,24(4):370-374.

[2]朱旭生,熊显萍,傅勇.一维可压缩欧拉解的爆破[J].华东交通大学学报,2009,26(2):111-114.

[3]ALI G,TORCICOLLO I.Global solutions to a hydrodynamical model for semiconductors in Lagrangian mass coordinates[EB/OL].[2010-01-15].http://www.na.iac.cnr.it/rapprti/2006/RT312-06.pdf,2006.

[4]YING L A,WANG CH.Global solution of the cauchy problom for a nonhomogeneous quasilinear hyperbolic system[J].Comm Pure ApplMath,1980,33(5):579-597.

[5]KATO T.The Cauchy problem for quasi-linear symmetric hyperbolic systems[J].Arch Rational Mech Anal,1975,58(3):181-205.

[6]TETU MAKINO,KIYOSHI,MIZOHATA,SEIJI UKAI.The Global Weak Solutions of the Compressible Euler Equation with Spherical Symnetry[R].日本:数理解析研究所,1992:1-28.

[7]DENIS SERRE.Systems of Conservation Laws[M].英国:剑桥大学出版社,2000:146-182.

[8]朱长江.Convergence rates to nonlinear diffusion waves for weak entropy solutions to p-system with damping[J].Science in China,2003,46(4):562-575.

[9]KENJI NISHIHARA.Boundary Effect on Asymptotic Behavior of Solutions to the p-system with Linear Damping[R].日本:数理解析研究所,1999:78-94.

[10]KENJI NISHIHARA.Lp-convergence Rate to Nonlinear Diffusion Wavea for p-system with Damping[R].日本:数理解析研究所,1999:95-113.

[11]JIALE HUA,TONG YANG.An improved convergence rate of Glimm scheme for general systems of hyperbolic conservation laws[J].Journal of Differential Equations,2006,231(1):92-107.

[12]LING HSIAO,TAO LUO,TONG YANG.Global BV solutions of compressible euler equations with spherical symmetry and damping[J].Journal of Differential Equations,1998,146(1):203-225.