小波多重分形在脑电信号分析中的应用
赵大庆 王 俊
1(南京邮电大学,图像处理与图像通信江苏省重点实验室,通信与信息工程学院,南京 210003)
2(南京邮电大学,图像处理与图像通信江苏省重点实验室,地理与生物信息学院,南京 210003)
引言
脑电图(electroencephalogram,EEG)作为客观反映大脑机能状态的一个重要方面,蕴涵着丰富的生理、心理和病理信息,通过对EEG信号的分析和处理,可以在临床上对一些脑疾病的诊断和治疗起到辅助作用。近年来,脑电信号的非线性动力学参数,如关联维、李雅普诺夫指数和近似熵等,已成功应用于脑功能状态及病理变化等方面的研究,证明了EEG信号的混沌性[1-2]。
小波用于对脑电信号的分析已有很多研究[3-4],分形用于对脑电信号的分析也有很多文献报道[5-6],但是小波和分形结合用来对脑电的分析还比较少。分形和小波相结合的方法发挥了小波多尺度分析和分形标度不变性两个特点,该方法在许多领域的奇异性分析中有很好的应用。因此,将分形和小波相结合的方法应用于脑电图的研究,可更加准确而深入地了解脑电信号的内在特征。
小波变换极大模值多重分形谱的方法一经提出[7],已经在很多领域得到应用[8-10]。本研究采用小波变换极大模值多重分形谱的方法,对健康青年人和老年人的脑电信号进行分析。研究发现,脑电信号具有奇异性质,脑电信号奇异谱的跨度会随着年龄的增大而减小。这可以用来检测目标个体是否出现脑衰退迹象,从而辅以进一步的临床干预措施。
1 理论和方法
1.1 多重分形谱
分形是对没有特征长度但具有一定意义的自相似性图形和结构的总称。多重分形是许多个单一分形在空间上的相互缠结、镶嵌,是单一分形的推广,单一分形可以看做是多重分形的一种特例。多重分形与单一分形一样,也是自相似的,与尺度无关。由每个测度的奇异性强度指数α和奇异谱f(q)构成了描述多重分形局部特性的奇异谱,f(q)也表示奇异性强度指数α所对应测度的分形维数。多重分形测度包括不同的奇异性强度,f(q)通常是分布于[αmin,αmax]之间的1个单峰图形,αmax相对于较强的奇异性,αmin相对于较弱的奇异性。计算多重分形谱可使用直接计算f(q)的方法,即标准盒计数法[11],这基于f(q)是一个特别测度的理论测度支架的维数。用尺寸为L的盒子来覆盖实验的测度,并且计算测度在每一个盒子中的概率,具体步骤如下:
1) 定义归一化概率为

式中Ti是某测度被分成N等份的时间序列中的第i份。
那么,构建在盒子中的概率重整化测度的单参量簇可表示为
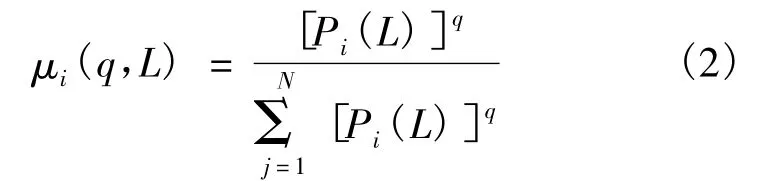
在一般维数的定义中,参量q提供了对奇异测度不同区域的微观探测。对q>1,μ(q)放大测度的强奇异区域;对q<1,μ(q)强调测度的弱奇异区域;而对q=1,μ(q)则复制原来的测度。
2) 计算μ(q)理论测度支架的Hausdorff维数f(q),有
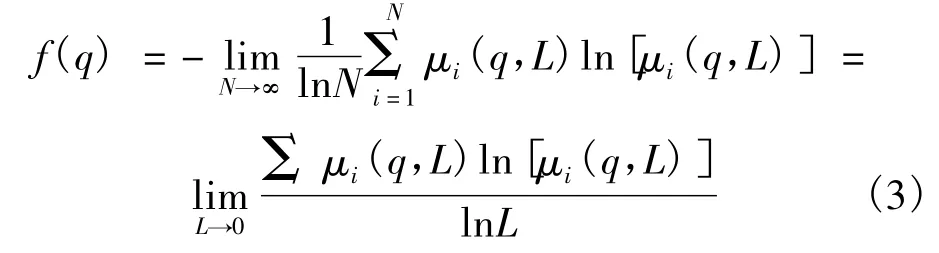
3) 计算μ(q)奇异强度αi=ln(Pi)/ln L的平均值 α(q),有

对应不同q,求出α-f(α)的单峰图像。
1.2 小波模极大值方法的多重分形谱
小波变换模极大值定义:在某一尺度χ0下,如果存在一点(x0,y0),使得,则称点(x0,y0)是局部极值点,且在y=y0上有一个模极大值(过零)点。如果对y0的某一邻域内的任意点 y,有 Wf(x0,y0)≤ Wf(x0,y0),则称(x0,y0)为小波变换模极大值点。小波变换的极大值的位置和大小包含了信号的主要信息[7]。
考虑用小波模极大值的方法求多重分形谱[7]。因为用小波模极大方法计算的多重分形谱能全面地反映信号的奇异性分布,而且,选择适当的小波函数还可以消除信号中平滑部分的影响,因此可以相信这种方法应该优于直接对信号求多重分形谱。小波模极大值法的多重分形谱计算过程如下:
1)对每一个尺度S计算出Wf(u,S)及其模极大值,随S的变化连接小波模极大值,得出模极大值序列。
2)然后用标准盒计数法对其模极大值序列进行分析,得出其多重分形谱。
2 实验与结果分析
使用 Neuroelectric and Myoelectric Databases[12],由于该数据库提供的总样本数限制,用了9位健康年轻人(年轻人脑电图见图1)以及9位健康老年人的脑电信号(老年人脑电信号图见图2)。从图1和图2两种人群的脑电信号图上可以看到,它们的幅度和形态都差不多,在时域上不能得到明显的区分。因此,需要寻找其在表面上还显现不出来的内在特征,寻找甄别不同脑功能状态的敏感特征参量。

图1 一位的年轻人的脑电信号图Fig.1 An EEG taken from one young subject

图2 一位老年人的脑电信号图Fig.2 An EEG taken from one old subject
截取长度相同的数据对其进行分析,为了视图清晰,只把其中3位年轻人和3位老年人的多重分形谱画出来(见图3)。从图3中可以看出,正常青年、老年EEG信号的奇异谱曲线都呈单峰拱形,这正是多分形信号的一个重要特征,说明正常青年、老年EEG信号都是多分形信号,都具有奇异性。
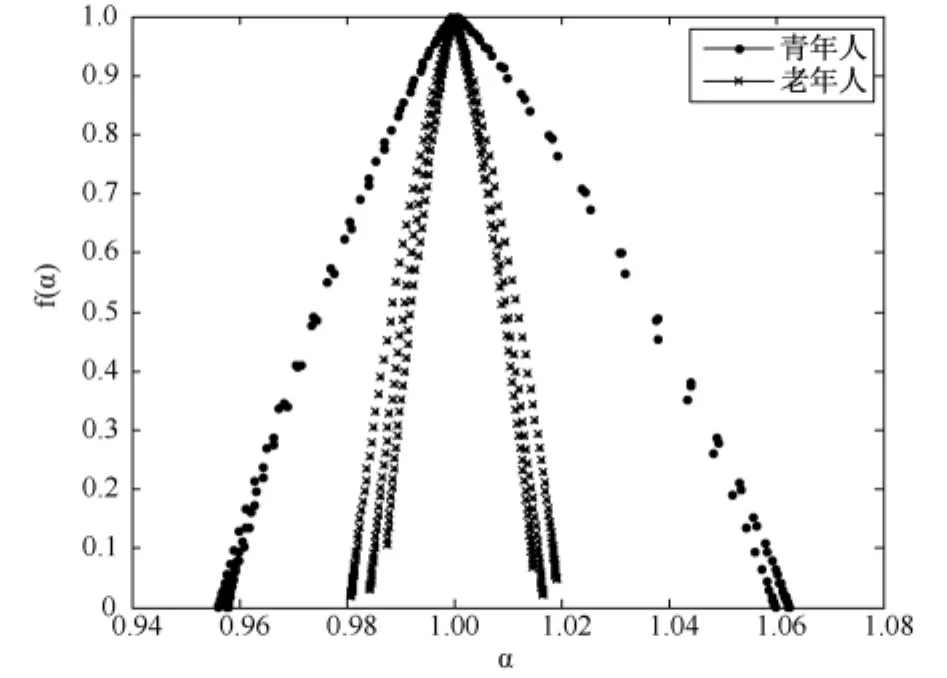
图3 3位青年人和3位老年人脑电信号多重分形谱对比Fig.3 Multifractal spectrum of EEG taken from 3 young subjects and 3 old subjects
表1和表2分别列出9个年轻人和9个老年人脑电信号的小波模极大多重分形谱奇异强度最大值、最小值和奇异强度区间大小详细数值,并且计算了两组研究人群的奇异强度的均值和标准差。
根据多重分形理论,每种尺度上都有最强波动和最弱波动,它们的标度指数 αmin和 αmax分别是α(q)中q→∞ 和q→-∞ 的结果。根据分形谱的宽度公式Δα=αmax-αmin,分别计算出两种信号的多重分形谱分布范围值,并对其进行样本均数比较的 t检验,得到 t=2.3443。查表可得,t0.05(9)=2.228。因为 t=2.3443 > t0.05(9),所以 P <0.05 差异有统计学意义。可以认为,年轻人EEG信号的Δα平均值明显高于老年人EEG信号的Δα平均值,从而可以区分开来这两种信号,因此Δα可以作为区分和识别这两种信号的一个标准。

表1 年轻人脑电信号多重分形谱Tab.1 The multifractal spectrum of young signals

表2 老年人脑电信号多重分形谱Tab.2 The multifractal spectrum of older signals
3 讨论和结论
由于大脑生理的复杂性,大脑功能体现出复杂的非线性动力学特性。本研究基于脑电信号的奇异特性,以及分形和小波相结合的方法,针对小波多尺度分析和分形标度不变性两个特点,用小波变换模极大值的多重分形方法,对健康青年人和健康老年人的EEG信号进行了分析和比较。研究发现,青年、老年人群的EEG信号的奇异度多重分形趋向于单重分形,预示着随着年龄的增长,大脑功能内在体现出的系统复杂度在趋于衰退。
随着社会老龄化的加剧,老年人群中患老年痴呆的比例在不断增大,给社会和家庭带来新的挑战和难题,及早地预测和定量大脑的衰退程度显得尤为重要。一般来说,脑电信号奇异谱的跨度会随着年龄的增大而减小,因此医生可以用目标个体的脑电信号的奇异度区间,与同年龄段大部分人的脑电信号的奇异度区间统计平均值正常波动范围进行对比,预先检测出目标个体是否出现脑衰退迹象,从而辅以进一步的临床干预措施,这对提高高危老年痴呆人群的生存质量具有重要的意义。
下一步的工作将致力于增大每个目标人群样本量的搜集,在大样本量的基础上,给出目标人群的小波模极大多重分形谱区间的变化范围。目前,对于脑衰退程度的定量研究还没有被充分重视,因此,深入进行这方面的研究,制定出科学的标准,对于诊断及临床干预和治疗脑衰退具有重要的意义。
[1]Acharya UR,Faust O,Kannathal N,et al.Non-linear analysis of EEG signals at various sleep stages[J].Comput Methods Programs Biomed.2005,80(1):37-45.
[2]江潮晖,冯焕清,刘大路,等.睡眠脑电的关联维数和近似熵分析[J].生物医学工程学杂志,2005,22(4):649-653.
[3]徐宝国,宋爱国.基于小波包变换和聚类分析的脑电信号识别方法[J].仪器仪表学报,2009,30(1):25-28.
[4]吴捷,张宁,杨卓,等.小波相干分析及其在听觉与震动刺激事件相关诱发脑电处理中的应用[J].生物物理学报,2007,23(6):482-487.
[5]Popivanov D,Jivkova S,Stomonyakov V,et al.Effect of independent component analysis on multifractality of EEG during visual-motor task[J].Signal Processing,2005,85(11):2112-2123.
[6]Wang Wei,Ning Bao,Wang Jun,et al.Interleaving distribution of multifractal strength of 16-channel EEG signals[J].Chinese Science Bulletin 48,2003,48(16),1700-1703.
[7]Muzy JF,Bacry E,Arneodo A.Multifractal formalism for fractal signals:The structure-function approach versus the wavelettransform modulus-maxima method [J].Physical Review E,1993,47(2):875-884.
[8]Kestener P,Arneodo A.Generalizing the wavelet-based multifractal formalism to random vector fields:application to three-dimensional turbulence velocity and vorticity data [J].Physical Review Letters,2004,93(4):044501-1-044501-4.
[9]苟学强,张义军,董万胜,等.基于小波的地闪首次回击辐射场的多重分形分析[J].地球物理学报,2007,50(1):101-105.
[10]芩为,杨世峰,薛蓉,等.基于小波变换模极大法的聚乙烯催化剂表面分形分析[J].中国科学 B辑,2007,37(4):374-379.
[11]Chhabra AB,Meneveau C,Jensen RV.Direct of the f(a)singularity spectrum and its application to fully developed turbulence[J].Phys Rev A,1989,40(9):5284-5294.
[12]National Institutes of Health.PhysioNet[DB/OL].http://www.physionet.org/physiobank/database/nesfdb/,2007-09-01/2010-06-10.

