运动声纳界面混响仿真研究*

周 晶 郝保安 陈亚林 胡 桥

(中国船舶重工集团公司第705研究所 西安 710075)

1 引言

水声设备在研制过程中由于受到各方面条件的制约,不可能经常进行海上或湖上试验,很多时候需要先进行仿真。混响仿真是声纳仿真技术中的一个重要研究领域,涉及研究内容十分广泛。海洋中存在不平整的海底和海面以及大量的散射体等,构成了实际海洋环境中的不均匀性、不连续的物理介质。当声波投射到这些不均匀介质上时就会产生散射过程,海洋中的大量非均匀介质的散射波在接收点上的总和构成所谓的混响场[1]。混响是声纳主要的背景干扰之一,它限制了声纳设备的作用距离。混响统计理论模型最初是由Faure提出,前苏联学者奥列雪夫斯基和美国学者Mid-Nemn就这一问题作了系统的讨论[2],并被称为FOM 混响理论模型,这种仿真较为粗糙。之后,有人把这些参数融入混响信号的时变功率谱中,通过对功率谱的转换以获得混响序列,但这种方法在实现的实时性上有一定困难[3～5]。当声纳载体有一定的运动速度时,不同方位对应的混响信号具有不同的多普勒频移,这使得混响的谱在较大的范围内扩展开,具有空时二维耦合的特性,更增加了声纳探测目标的难度。因此研究运动声纳混响信号仿真方法,对提高声纳设备目标探测性能有重要意义。

本文提了一种基于空间非均匀分布散射元信号合成的运动声纳混响信号仿真方法,该方法既能比较全面地考虑发射信号、海洋环境等混响的各种影响因素,又能自然地保持空间相关性,体现出混响频率随空间方位的变化关系。这种方法能够得到任意阵形所有阵元的混响仿真信号,可满足某些降维自适应信号处理方法研究的需要,并且通过波形伸缩可以得到任意复杂信号的混响仿真信号,具有较强的通用性。

2 混响仿真模型

混响是一个很复杂的随机过程,受到多种因素的影响,为使混响建模切实可行,需要做一些简化假设。由于混响随距离衰减很快,通常在相对较近的距离条件下才起主导作用,所以一般混响的仿真距离不用太远[6～7]。为简化计算,本文作如下假设:

1)任一瞬间在仿真散射单元空间内的散射体是随机均匀分布的,且每个散射体有相同的贡献;

2)不考虑多次散射,只考虑散射元的一次散射;

3)在一个脉冲宽度的时间内,忽略由于平台运动引起的散射元和接收单元的空间方位变化量;

4)散射体只在原位置作方向随机运动。

考虑如图1所示的情形,声呐平台以速度V沿着X轴运动,以海底混响为例进行分析。设距离海底H的发射声波的波长为λ,基阵轴向Y与向量V垂直,海底某混响散射体相对于轴向的入射锥角为α,相对于速度方向的入射方位角为θ,相对于XOY坐标平面的夹角为俯仰角φ,如图1所示。于是海底某散射单元的多普勒频移为

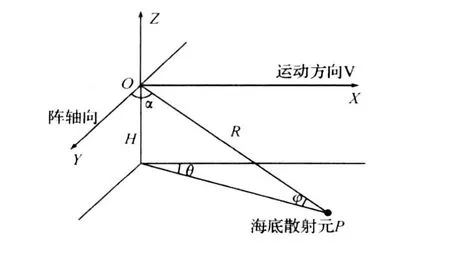
图1 散射元分布位置图

由图1可得cosα=sinθcosφ,将其代入式(1),即得多普勒频移

其中fnmax=2V/λ为最大多普勒频移。对于CW情形,发射信号形式为

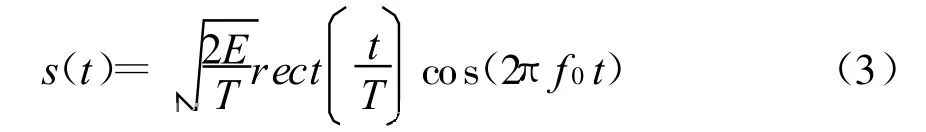
式中:E为发射能量;T为发射脉宽;f0为发射中心频率;rect(◦)为矩形包络。则根据式(2)可得CW信号的混响空时二维分布,如图2所示,平台运动速度相同时,随着发射频率的增大,接收回波信号产生的多普勒频移也随之增大。

图2 不同频率的CW脉冲信号的多普勒频移

3 混响仿真信号及其特性

3.1 混响信号仿真方法

以位于坐标原点O的第m个阵元接收为例,第n个散射元P的方位角和俯仰角分别为θ和φ,到原点的距离为R,设声纳的发射信号频率为f0,脉宽为τ,其发射信号复包络为 E(t)(0≤t≤τ),则该阵元的混响信号应为所有散射元反射信号的叠加:

式中fn为n个散射元的多普勒频移;c为声速;Nr为所有散射元的个数;n(t)为随机的幅度及相位调制信号,它的起伏大小决定了该散射元的多普勒扩展的程度,由于界面和海水中具有大量的微小散射体,仿真时位于某一位置的散射元其实也包含着许多的微小散射体,这些散射体又都在作随机运动,其后果就将导致某一散射元的反射波也有一定的起伏,n(t)就是这一起伏的反映,通常认为,n(t)是具有高斯型功率谱的随机信号,其谱的宽度反映了回波多普勒扩展的程度;pn为第n个散射元的回波平均幅度,与发射信号强度、散射元散射强度及其所代表的面积或体积、发射和接收的波束指向性、传播扩展衰减和海水吸收等有关;对于不同的接收阵元,式(4)中rn是变化的。

仿真得到混响信号如图3所示,发射信号为CW信号,频率为20kHz,设置海深为400m,声纳放置在距海面100m的位置处,将接收回波仿真信号按一定角度划分成若干个区域,假定每个角度范围的散射体个数是一致且均匀分布的,这样随着距离的增大,散射体在整个范围内就是非均匀分布的。

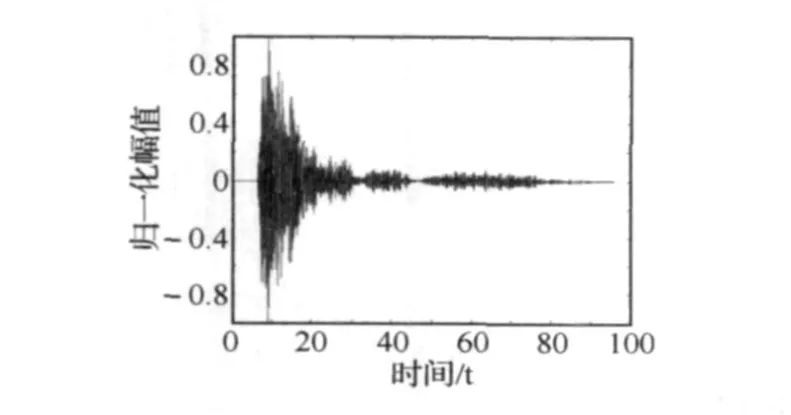
图3 混响信号仿真结果

3.2 混响信号概率密度特性

混响的瞬时值满足高斯分布,混响信号的包络服从瑞利分布,相位服从均匀分布。

混响瞬时值概率密度函数为[8]:

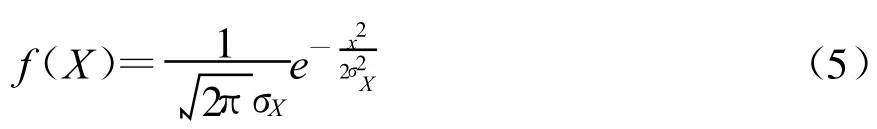
式中:σV是瞬时值 V的方差。

将混响表示为如下形式:

式中:E(t)为混响的慢变包络,φ(t)为混响信号的相位。则混响信号的概率密度函数为:

混响的相位服从均匀分布:

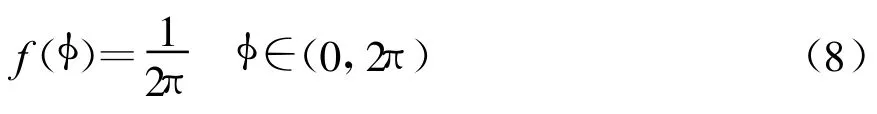
图4是仿真结果在多次平均的基础上得出的混响信号瞬时值、相位和包络的概率密度实际仿真值。仿真结果表明,基本符合上述理论分析结果,即混响信号瞬时值符合高斯分布,而包络符合瑞利分布,相位服从均匀分布。

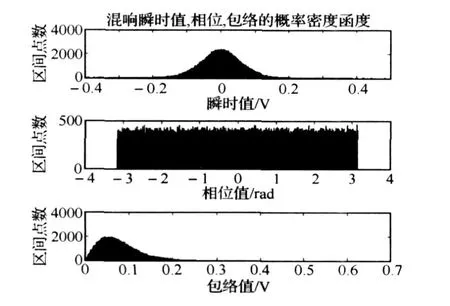
图4 概率密度函数分布

3.3 混响仿真信号的时间相关特性

混响的时间相关是由一个混响信号的自相关函数描述的,如果混响信号为:

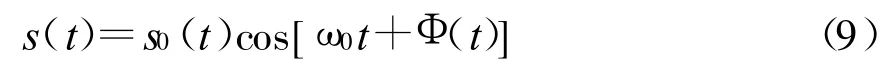
式中:s0(t)为信号包络,ω0为信号频谱的中心频率。

图5为仿真信号选取一个通道接收混响信号的时间相关性仿真图,图(a)发射信号频率为20kHz,图(b)发射信号频率为22kHz。混响的时间相关半径随发射信号频率的变化有很好的一致性,混响的时间相关半径随发射信号频率的增大而减小。

图5 时间相关性图

3.4 混响仿真信号的空间相关特性

混响信号空间相关系数的理论表达式为:

式(10)水听器水平指向性开角:

水听器到海底的深度h,作用距离为r,水听器间距为l。

设两个阵元接收的混响信号为X(t)和Y(t),则这两个阵元的混响信号的空间相关系数为:

图6为界面混响情形下仿真混响信号各通道的相关系数图,随接收阵元间距的增大表现为振荡衰减的形式并最终消失,仿真结果与理论分析结果也有较好的一致性。

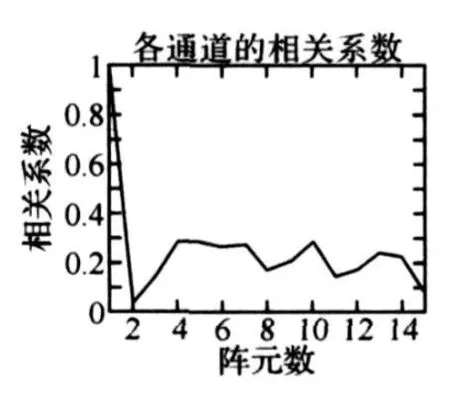
图6 空间相关性图

4 结语

本文采用一种直观,易于实现的方法完成了运动声纳混响信号的仿真。综合考虑了发射信号形式、声纳运动特性、海洋环境等多种混响影响因素,实现了对运动声纳信号的直观、简便仿真。通过对仿真信号瞬时值和包络值概率密度分布、空间相关系数进行了检验,结果证明了仿真的有效性。该仿真方法除了能够比较完整细致的模拟混响的各种统计特性外,还能够自然地保持阵元间的空间相关性。

[1]R.J.尤立克.水声原理[M].洪申,译.哈尔滨:哈尔滨船舶工程学院出版社,1990:190～215

[2]蔡平.界面混响信号的仿真研究[J].哈尔滨工程大学学报,2000(4):31～35

[3]徐新盛,张燕,李海森.海底混响仿真研究[J].声学学报,1998(2):141～148

[4]William H.An Oceanic Reverberation Model[J].IEEE Journal of Oceanic Engineering,1984,9(2):63～72

[5]何心怡,张鹏.鱼雷混响建模与仿真研究[J].舰船科学技术,2008(2):169～171

[6]PaulC.Etter.水声建模与仿真[M].北京:电子工业出版社,2003:274～286

[7]D.Middletion.A Statistical Theory of Reverberation and Similar First-order Scattered Fields PartⅠ[J].IEEE Trans,1967(13):372～392

[8]B.B奥里雪夫斯基.海洋混响的统计特性[M].北京:科学出版社,1977:67～139