一种应用于LTE系统的Viterbi译码算法*

李小文，罗友宝

（重庆邮电大学通信与信息工程学院 重庆 400065）

1 引言

在通信系统中，发送端发出的信号不可避免地要受到随机噪声和突发噪声的影响，信号的传输波形若受到破坏，则会使接收端可能发生错误判决。消除或降低噪声干扰的方法包括均衡、提高发射信号功率等，但是这些方法通常不能满足传输要求。

信道编码是现代通信系统广泛采用的一种差错控制措施。利用将“数据序列”转变成“更好的序列”产生冗余比特，这些冗余比特可以用于检测错误和纠正错误。

卷积码是信道编码中最为重要的一类。根据卷积码码字是否以零比特结尾，可以分为零尾比特卷积码(zero-tail CC)和咬尾卷积码(tail-biting CC)。零尾比特卷积码有固定的结尾清零比特作为结束状态，译码相对较简单；咬尾卷积码没有结尾清零比特，编码时使用数据块的最后m个信息比特来初始化编码寄存器，使编码器的初始状态和结束状态相同，这样做可以提高编码效率，节约带宽资源，但对译码器来说初始状态和结束状态都是未知的，因此也增加了译码复杂度。

目前，在咬尾卷积码Viterbi译码方面的研究主要有以下的情况。

[1]提出了一种自适应的循环Viterbi译码算法，并且提出了3种不同的译码结束规则，不同的结束规则，译码计算复杂度和译码BER(bit error rate，误比特率)不同。

·参考文献[2]基于编码判决深度，利用Viterbi译码的收敛性，提出了一种优化的循环Viterbi译码算法。

·参考文献[3]基于译码复杂度的考虑，提出了一种改进的Viterbi译码算法，此算法可以将译码计算复杂度降到很低的水平。

·参考文献[4]基于Viterbi译码的码块迭代思想，提出了一种环绕Viterbi译码算法，且在此基础上提出了一种并行译码的双向Viterbi译码算法。

·参考文献[5]提出了一种改进的环绕Viterbi译码算法，该算法在每个码块译码结束时都判断当前码块及之前码块是否满足译码输出条件，通常迭代较少次数就可以得到正确译码。

本文第二部分介绍LTE系统中的咬尾卷积码，第三部分详细分析几种现有的咬尾卷积Viterbi译码算法，主要分析它们的译码原理和译码计算复杂度，并提出改进的Viterbi译码算法；第四部分对几种算法进行仿真，并对仿真结果进行分析，通过对BER及译码计算复杂度进行比较，评判译码性能的优劣。

2 LTE系统中的咬尾卷积码

LTE作为准4G技术，以OFDM(orthogonal frequency division multiplexing，正交频分复用)和MIMO(multipleinput multiple-out-put，多输入多输出)技术为基础，下行采用正交频分多址技术，上行采用单载波频分多址技术，在20MHz频谱带宽下能够提供下行100Mbit/s与上行50Mbit/s的峰值速率，降低了系统延迟。

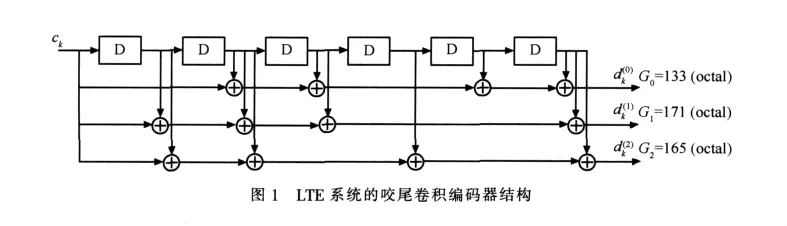
LTE系统采用咬尾卷积码和Turbo码来实现前向纠错[6]，其咬尾卷积编码器结构如图1所示，它的限制长度为7，编码速率为1/3，使用码块的最后6 bit信息来初始化6个编码移位寄存器，促使编码器的初始状态和结束状态相同，从而提高编码效率。

3 咬尾卷积码Viterbi译码算法

与传统的Viterbi译码不同，咬尾卷积Viterbi译码不知道编码器的初始状态和结束状态，因此，译码难度增加。本文主要讨论咬尾卷积码的循环Viterbi译码(circular viterbi algorithm)和环绕Viterbi译码 (wrap-around viterbi algorithm)。在以下的讨论中，m表示编码器移位寄存器的个数，K表示码块的长度。

3.1 循环Viterbi译码(CVA)

参考文献[1]提出的循环Viterbi译码算法可以说是很多改进循环Viterbi算法[2～5]的基础，其基本思想为：将接收到的码块重复连接，对连接后的长序列进行Viterbi译码，即译码器任意选择一个初始状态或从所有初始化度量相同的状态开始进行VA译码的ACS(add-compare-select，加比选)计算，这样前一个码块的可用信息将传输到后一个码块并在后一码块中累积，每个码块的可用信息将不会被浪费。同时，参考文献[1]也提出了固定的译码结束规则和可变的译码结束规则以及二者兼顾的译码结束规则，不同的结束规则有着不同的译码性能，这在后来的改进算法中都有所体现。

为了提高译码性能，降低译码复杂度，减少译码延迟，参考文献[2]和[3]分别提出了BDD-CVA译码算法和Lw-CVA译码算法，它们都有固定的译码时间，且通常只需将接收码块部分重复。以参考文献 [2]提出的BDD-CVA算法为例，其算法描述为：

a.初始化所有(个)开始状态的度量值，一般设置为0；

b.从开始的个状态做VA译码的ACS操作，执行到时刻t=Linit；

c.在t=Linit时刻选择路径度量最小的节点，清除其他节点的路径，然后从选择的节点继续VA译码的ACS操作，直到 t=(2Linit－1)mod K 时刻；

d.译码输出t=Linit时刻的数据符号，然后继续向后以Lf(Lf≤Linit)为窗滑动做VA译码的ACS操作K－1个时刻，到达t=(Linit+Lf+K－2)mod K时刻，并译码输出剩下的K-1个数据符号。

其中Linit、Lf以及后文即将提到的win的具体取值可以参见参考文献[7]。换个角度看，BDD-CVA可以看作没有滑窗，而是将码块重复了Linit+Lf-2个时刻，译码输出数据为长码流的中间K个数据符号。参考文献[3]提出的算法(Lw-CVA)与此相似，但它省略了在t=Linit时刻选择最小路径度量节点，清除其他节点的操作，这在参考文献[2]中也有所提到，且在实际应用中是可容许的，它先将码块重复Linit+win个时刻，对长序列码块做Linit+K+win个时刻的VA译码，然后选择最优路径回溯，回溯输出中间K个时刻的数据作为最终的译码输出。可以看出Lw-CVA实质为BDD-CVA的简化，如果把常数2加进Lf，则以上两种算法就相同了，因此它们的译码性能也几乎是相同的。

以上循环Viterbi译码算法的共同点都是先将译码初始状态收敛到正确路径，这样就必然导致要将码块部分重复(当Linit+win﹤K时)，然后才译码输出，最后将译码输出调整到正确位置，它们的译码计算复杂度均约为(Linit+K+win)×2m。

3.2 环绕Viterbi译码(WAVA)

参考文献[4]提出了一种环绕Viterbi译码(WAVA)算法，其算法描述为：

a.初始化所有(2m个)初始状态的度量值，设置为0；

b.从开始的2m个状态做VA译码的ACS操作，迭代完第一个码块后，检查最优路径的首末状态是否相同，相同则停止译码，输出译码序列，否则进入下一步；

c.用上一次迭代结束的所有状态度量来初始化当前迭代的所有初始状态的度量，然后进行VA译码的ACS操作，当前码块迭代完成后检查最优路径中当前码块首末状态是否相同，相同则输出当前译码序列，停止译码，否则进入下一步；

d.重复上一步，直到最优路径的首末状态相同，或迭代次数达到最大；

e.如果最优路径的首尾状态不相同，则判断其他路径是否首尾状态相同，如果找到这一路径，则输出对应的码字，否则输出具有最优度量的路径。

一般情况下，迭代次数越大，译码性能越好，但同时译码延迟也随之增大，因此迭代次数也是有上限的，对于不同系统的应用，应综合考虑译码BER和译码延迟，从而设定合适的迭代次数。参考文献[5]提出了环绕Viterbi译码算法的一种改进算法——L3-WAVA，与WAVA的不同之处在于：在第个码块迭代计算法结束时，它不仅检查最优路径Plmax(l=1,2,…,L，L为最大迭代次数)的当前码块l的首末状态是否相同，而且还要检查之前的各码块(l-1,l-2,…,1)的首末状态是否相同，只要有一个码块的首末状态相同，则输出相应码块的译码数据，否则继续迭代，直到达到迭代的最大次数，若仍无首末状态相同的码块，则输出第骔L/2」+1个码块的译码数据。

以上两种WAVA算法都是基于码块迭代思想，同时利用Vitrbi译码的收敛性，以判断各个码块的首末状态是否相同来确定译码输出，如果迭代达到最大次数，则输出指定码块的译码数据作为最终的译码输出，译码计算复杂度均约为（l×K）×2m，（l=1,2,…,L），这样码块经过多次迭代，各码块携带的信息在后来的码块累积，可以降低译码BER，但由于在译码输出之前通常需要迭代多次，所以BER的降低是以计算复杂度的增加为代价的。

3.3 改进Vitervi译码算法(Cd-CVA)

由于LTE系统要求提供更高的数据传输速率，在保证传输可靠性的同时必须尽可能地降低译码延迟，因此综合考虑译码BER和译码延迟，同时利用Viterbi译码的收敛性和编码判决深度思想，以及WAVA检查各个码块首末状态的方法，现在Lw-CVA的基础上进行改进，提出一种改进的循环Vitebi算法(Cd-CVA)，其算法示意如图2所示，图中虚线部分表示可能不会经历的步骤。

算法描述如下：

a.初始化所有(个)开始状态的度量值，设置为0；

b.从开始的个状态做VA译码的ACS操作，执行到时刻t=(K+Ld)mod K；

c.在t=(K+Ld)mod K时刻选择最优路径回溯，回溯到t=0时刻，检查t=0时刻和t=K时刻的状态是否相同，相同则译码输出，否则，接着步骤b继续执行VA算法ACS，直到t=(K+Lc+Ld)mod K时刻；

d.在t=(K+Lc+Ld)mod K时刻选择最优路径回溯，回溯到t=0时刻，得到最优路径的状态序列state_sequence(1,K+Lc+Ld)，用状态序列的第K+1,K+2,…,K+Lc个值取代第1,2,…,Lc个值，最后译码输出状态序列的前K个值，作为最终译码输出。

其中，Lc为纠正深度，Ld为编码判决深度[7]，通常我们取Lc、Ld为限制长度的4～6倍，Ld≤Lc，稍微增大或减小Lc、Ld值的大小，如加 1或减 1，对译码 BER不会造成重大影响。由于回溯一次的时间远小于加比选操作的时间，因此,此改进算法的译码计算复杂度平均略小于(K+Lc+Ld)×2m。

在t=(K+Ld)mod K时刻回溯一次是非常有必要的，这是利用了参考文献 [1]中提到的K+m算法给出的一种思想，即只在码块的末尾重复一小部分时，原码块的首末状态可能已经相同了，尤其是信噪比大的情况下，此时如果回溯路径首末状态相同，则译码输出是正确的，如果回溯路径首末状态不相同，则路径的前Lc个状态的错误率最大，因此必须在K+m算法的基础上采取纠正措施，即执行改进算法中的步骤d，最后将路径中错误的状态替换掉，保证路径的首末状态相同，从而提高译码的正确性。

4 仿真验证及性能分析

通过仿真各种算法的BER，结合各算法的译码计算复杂度，比较各算法的性能优劣，为LTE系统的实际应用提供有力佐证。

4.1 仿真条件设置及仿真模型

由于在LTE系统中，咬尾卷积编码主要用于PBCH（物理广播信道）、PDCCH （物理下行控制信道）、PUCCH（物理上行控制），编码前的数据主要是控制信息和调度信息，其数据量一般都不大，LTE Release8协议没有明确规定码块的最大长度，但在LTE协议的提案中已经提出咬尾卷积码的最大码块大小为200 bit，大于200 bit时则采用Turbo编码[8]。据此，为了适合大多数情况，在仿真中设置码块的大小为150 bit，每次对5 000个数据块进行仿真统计，假设调制方式采用BPSK调制，信道为加性高斯白噪声(AWGN)信道，仿真模型如图3所示。

4.2 仿真结果分析

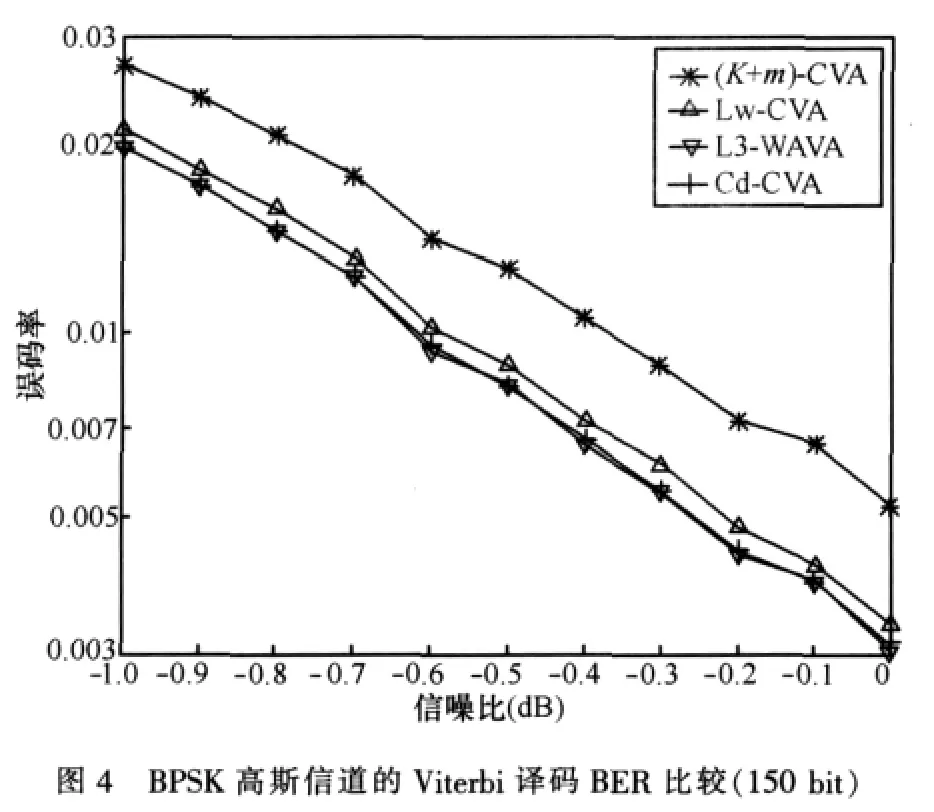
图4同时对K+m算法，BDD-CVA的改进算法Lw-CVA，WAVA的改进算法L3-WAVA以及文章中提出的新改进算法Cd-CVA进行了仿真比较，为了便于比较，Linit、win、Lc、Ld 的取值均为 4(m+1)，L3-WAVA 的最大迭代次数取值为L=3。可以看出,由于K+m算法没有采取错误纠正措施，且m﹤Ld，其BER明显是最大的；Lw-CVA算法次之，改进算法Cd-CVA的BER在Lw-CVA的基础上有了明显的降低，且改进算法Cd-CVA的译码计算复杂度平均略小于Lw-CVA算法的译码计算复杂度；同改进环绕Viterbi译码算法L3-WAVA相比，改进算法Cd-CVA几乎与之有相同的BER，但是改进算法Cd-CVA的译码计算复杂度却大大降低，如果L3-WAVA迭代3次才译码结束，则改进算法的译码计算复杂度约为L3-WAVA的1/2。

对于码块长度更小的情况，每个码块携带的可用信息量减少，因此，为了保证译码的正确性，可以将纠正深度和编码判决深度的取值增大。图5为码块长度为40 bit，Linit、win、Lc、Ld 的取值均为 6(m+1)的仿真 结 果 ，可以看出，即使码块更小，改进算法的BER仍然比Lw-CVA算法的BER低，与L3-WAVA几乎相同。因此，根据咬尾卷积码码块长度的不同，纠正深度和编码判决深度的取值应有所不同，在LTE实际应用中可根据不同的信道自适应变化，以适应不同信道的译码需求。

通过以上分析，改进算法不仅降低了译码计算复杂度，译码的误比特率也可以得到较好的效果，因此非常适合LTE系统的要求，可以应用于LTE系统实现。

5 结束语

LTE系统要求提供速率更高的数据业务，因此对系统的实时性要求也更高，本文针对LTE系统对高速数据业务以及数据传输高可靠性的要求，对现有的Viterbi译码算法进行了详细分析，并综合考虑译码时延与译码的正确性，利用现有算法的优点，提出了新的改进算法并进行了仿真验证，仿真结果表明，改进算法有着更好的译码性能，因此LTE系统采用本文提出的改进译码算法来实现具有较好的译码性能，值得推广应用。

参考文献

1 Richard V,CoxAn C,Sundberg W.An efficicent adaptive circular viterbi algorithm for decoding generaliized tailbiting convolutional codes.IEEE Transactions on Communications,1994,43(1):57～68

2 John B A,Stephen M H.An optimal circular viterbi decoder for the bounded distance criterion. IEEE Transactions on Communications,2002,50(11):1736～1742

3 中兴通讯股份有限公司.一种咬尾卷积码的译码方法及其译码器.中国：200510011625,2006

4 Rose Y,Shao Shulin,Marc P C,Fossorier.Two decoding algorithms for tailbiting codes. IEEE Transactions on Communications,2003,51(10):1658～1665

5 华为技术有限公司.咬尾卷积码的译码方法和装置.中国：200810148828,2009

6 3GPP TS 36.212 v8.7.0.Multiplexing and channel coding(release 8),2009

7 Anderson J B,Balachandran K.Decision depths of convolutional codes.IEEE Transactions on Communications,1989,35(2):455～459

8 Motorola,France Telecom,GET,et al.EUTRA FEC Enhancement(R1-061050).ftp://www.3gpp.org,2006