确定性复杂网络的稳定性受随机打击影响的研究

畅兴平，夏清华

（襄樊学院物理与电子工程学院 襄樊 441053）

1 引言

复杂系统广泛存在于自然界和人类社会中，如中国城市航空网络、公交停靠站点网络、中国百强电子销售网络、科研合作网等，对这些复杂系统的研究已引起人们极大的兴趣。对它们稳定性的研究尤为重要，因为复杂网络的稳定性直接影响到信息的拥塞、传输、抗外界干扰。如路由器分布网络[1],我们想要信息能够更准确、更迅速地到达目的地，就必须使它的分布网络更优化；如果想要它受外界影响更少，则可以改变它的网络分布模式，寻找一个更好的网络模型来代替以前的网络。系统网络的好坏通常是利用这个系统网络的稳定性来衡量的[2]。为此，本文对陈牧先生提出的确定性复杂网络模型的稳定性利用随机打击进行了分析。

2 确定性复杂网络模型

复杂网络模型的演化过程经过了4个阶段，随机网络（random graph）模型、小世界网络 (small-world)模型、无标度网络(scale-free)模型和确定性复杂网络模型。无标度网络模型[3]（BA模型）最接近于现实存在的网络，因此，此模型能够很好地模拟现实中的度取值范围和概率分布。但是BA模型也有不足的地方[4]，其缺陷有以下几方面：网络的生长过程是多种多样的，很难预测，而它忽略了增长中的复杂性；优先连接中的概率取值过于简单；没有考虑网络中有向性问题及各条边的权重；BA模型网络生长过程采用不间断方式，这对现实中的网络很难做到。为了解决上述模型存在的问题，2007年，陈牧引入了一种同时拥有小世界效应和无标度特性的确定性网络模型,如图1所示。

确定性复杂网络的构造方法如下[1]：

（1）从n=0开始，即从一个节点出发；

（2）当n=1时，在第一个节点下方的两边对称地分布两个节点，且使这两个节点与第一个节点相连；

（3）当n=2时，用相同的方法，在新生长出来的两个节点的下方分别再对称生长出两个节点。且这4个节点再与第一个节点相连。

依照这种方法不断地生长下去，就得到了一个确定性的网络。可知，整个网络的总节点数为N(n)=2n+1-1，总边数为E(n)=(n-1)2n+1+2，也可以求得节点增长和边的增长关系为 ΔE(n)=E(n)-E(n-1)=ng[N(n)-N(n-1)=ngΔN(n)，其平均度为

由图2可以看出，随着网络的不断增长，确定性复杂网络模型的平均路径长度近似为2，为一个衡量，且网络的平均路径长度总体较小。

此外，确定性复杂网络的群系数与网络大小的关系[1]如图3所示。

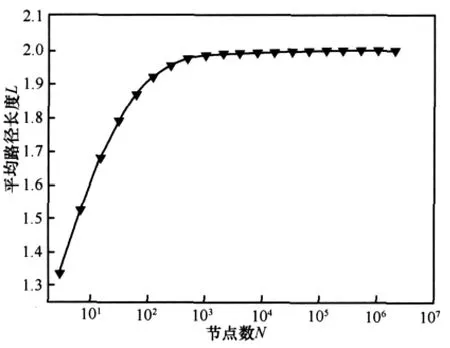
图2 平均路径长度与网络大小的关系

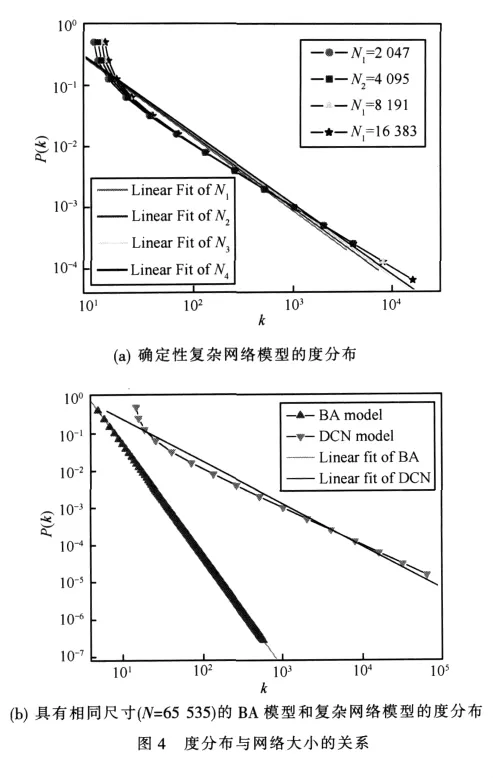
N指确定性复杂网络中的节点数，由图可知当N达到一定数量后，群系数C增长缓慢且趋近于1，群系数的整体变化范围很小。图4是度分布与网络大小的关系。其中，确定性复杂网络模型的度分布（N1=2 047,N2=4 095,N3=8 191,N4=16 383）幂指数分别满足 γ1=1.2012,γ2=1.18552,γ3=1.17146,γ4=1.15887。

3 随机打击对确定性复杂网络的稳定性影响

确定性复杂网络同时拥有小世界效应[5]和无标度特性，它的等级结构解释了中枢节点在复杂网络中的角色：层数越高，其中的节点度越大。这些中枢节点对于维持确定性复杂网络的完整性起到主导作用。然而，它们直接连接的节点表现得彼此疏远，无凝聚力，从而导致了取值较小的部分[6]。另外，这些连接数少的节点具有很大的群系数，这也意味着它们的邻居密集连接，并形成了小的集群。每个节点与其亲属节点连接，确定性复杂网络的抗毁性得到增强。随机打击是研究网络稳定性时经常用到的一种方法，都是通过计算机模拟来实现的。本文中主要的亮点是使用了蒙特卡洛方法，这为以后复杂网络稳定性的研究开辟了一个新颖的研究道路。

打击的主要思路：放一个随机粒子在确定性复杂网络的正中间，取一个0～1之间的随机数，让这个粒子随机行走，步长是1（假设节点之间的距离都是1），每走一步打击到一个粒子，且这个粒子就不存在了，再算剩下来网络的平均路径长度和群系数。直到粒子碰到边界为止。这里取n=21层网络进行网络稳定性分析，此时N(20)=2 097 151，L=1.99996。随机打击的示意如图5所示。

3.1 在随机打击下平均路径长度的变化

确定性复杂网络的构造是很规则的，并且有很强的层次感，假设i代表层数，则经过n次迭代以后可得：第i行第j个节点的路径为，整个网络的平均路径长度为，n层网络的总节点数N(n)=2n+1-1。打击掉第i层第j个节点后，网络的平均路径长度为：

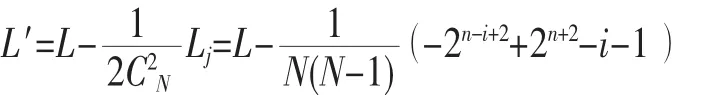
显而易见，只要知道第几层，几个节点，很容易就可以求得打击节点后的确定性复杂网络的平均路径长度，这个值是随着i值和打击节点个数变化的。在随机打击中，利用的是随机因子，并且随机数不同，打击后的节点的表达式也有相对应的变化，但都和i有关系。

利用计算机编程进行模拟，再根据上面讲的打击思路对网络进行打击，可得到一系列的数据。打击后的节点数N与平均路径长度L的关系如图6和图7所示。

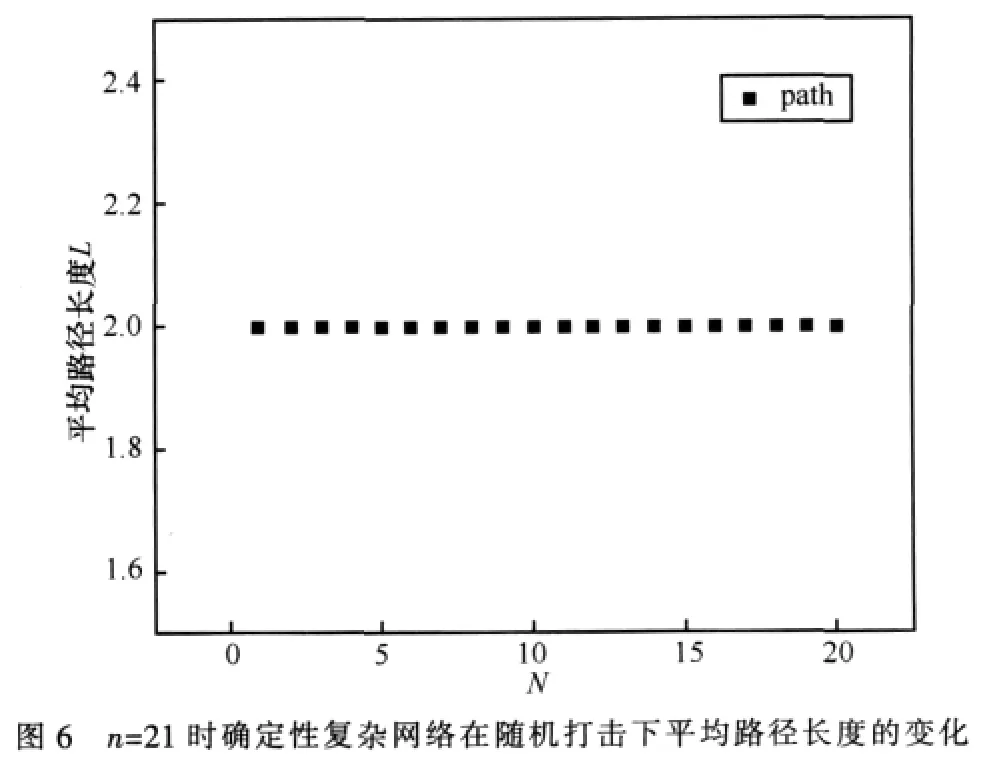
图6中横坐标是确定性复杂网络的层数n，纵坐标是平均路径长度。从图中可以看到，平均路径长度从1.99996到1.99991，几乎没有变化，也可以说确定性复杂在随机打击下平均路径长度并没有受到很大影响。而网络层的多少对平均路径长度的影响只是轻微的，总的效果没有发生什么改变。图7是n=21和n=13两种情况下的n和L的关系图，由图可以得到，网络层越多，节点数越大，网络越稳定，抗毁性越强。

图8是确定性复杂网络的f与L的关系图，其中f是打击的节点数与总节点数的比值。由图可知，随着f的增加，平均路径长度L逐渐减小，变化范围从1.8267到1.9983，范围很小，因此确定性复杂网络是比较稳定的。

3.2 在随机打击下群系数的变化

群系数同平均路径长度一样，是衡量复杂网络稳定性的另一个非常重要的量，同样的方法可求得n层迭代以后的群系数。

第i层第j个节点的群系数：

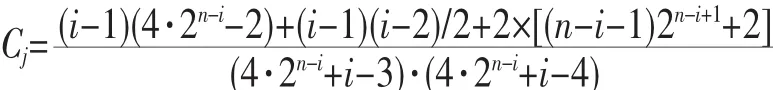
总群系数C为：

显而易见，只要知道n、i和打击的节点数，就可以很容易地得到打击后的群系数。

图9中横坐标是确定性复杂网络的层数n，纵坐标是群系数C。从图中可以看出群系数几乎是一条直线，在0.951附近，所以确定性复杂在随机打击下群系数并没有受到很大影响。

由图10可知，网络节点多的群系数大，节点小的群系数小。但它们受随机打击后的群系数C并没有受到很大的影响，还是比较稳定的。

图10 n=20和n=13时确定性复杂网络在随机打击下C的变化

4 结束语

在随机打击下，确定性复杂网络的平均路径长度和群系数都能保持很好的稳定性，没有因随机打击而受到很大的干扰，所以确定性复杂网络对于随机打击具有很强的稳定性。

1 Chen Mu,Yu Boming,Xu Peng,Chen Jun.A new deterministic complex network model with hierarchical structure.Physica A:Statistical Mechanics and its Applications,2007，385(2):307～317

2 Barabási A L,Albert R.Emergence of scaling in random networks.Science,1999（286）:509～512

3 杜海峰，李树茁.小世界网络与无标度网络的社区结构研究.物理学报，2007,56(12)：6886～6893

4 Boccaletti S.Complex networks:structure and dynamics.Physics Reports,2006(424):175～38

5 Watts D J,Strogatz S H.Collective dynamics of “small-world”networks.Ature,1998（393）：440～442

6 Barbási A L,Jeong H,Jeong H,Ravasz E,et al.Evolution of the social network of scientific collaborations.Physica A,2002（311）:590～614