基于知识点约束的遗传算法组卷策略的研究

耿 霞

(天津市信息中心，天津 300201)

遗传算法GA(Genetic Algorithm)是一种模拟自然界生物进化过程的随机搜索、优化方法。它是模拟达尔文的遗传选择和自然淘汰生物进化过程的计算模型[1]，采用简单的编码技术来表示各种复杂的结构，并通过一组编码表示简单的遗传操作和优胜劣汰的自然选择来指导学习和确定搜索的方向。由于遗传算法采用种群的方式组织搜索，这使得它可以同时搜索解空间内的多个区域，而且用种群组织搜索方式使得其特别适合大规模并行。目前，该算法已渗透到许多领域，并成为解决各领域复杂问题的有力工具。

1 遗传算法用于组卷的优势

作为一种优化与搜索算法，遗传算法相比于其他算法应用于组卷系统所具有的优势在于[2]：

(1)遗传算法的操作对象是一组可行解，而非单个可行解，搜索轨道有多条，而非单条，因而具有良好的并行性。

(2)遗传算法只需要利用目标的取值信息，而无需梯度等高价值信息，因而适用于任何大规模、高度非线性的不连续多峰函数的优化以及解析式的目标函数的优化，具有很强的通用性。

(3)遗传算法择优机制是一种“软”选择，加上其良好的并行性，使它具有良好的全局优化性和稳健性。

(4)遗传算法操作的可行解是经过编码化的，目标函数解释为编码化个体的适应值，因而具有良好的可操作性和简单性。

2 基于遗传算法的组卷策略

组卷中决定一道试题，即是决定1个包含有试题唯一标识(ID)、题型、难度、区分度、考核点、考核点类型、能力层次、建议分值的 8 维向量(a1，a2，a3，a4，a5，a6，a7，a8)，决定一份试卷 n道题，就决定了 1个 n×6的矩阵S：

这就是问题求解中的目标状态矩阵。建立问题的目标矩阵后，依据遗传算法的基本流程，对本研究的组卷策略进行详细阐述。

2.1 染色体编码及群体的初始化

用遗传算法求解问题，首先要将问题的解空间映射成一组代码串[3]。有文献用二进制编码，用1表示该题被选中，0表示未被选中。这种编码简单明了，但是进行交换等遗传操作时，各题型的题目数难以精确控制。当题库中题量很大时，编码冗长。已有大量实验表明，在解决数值优化问题时，采用实数编码的遗传算法的效率要好得多，因此，本研究采用实数编码。在组卷中所得的可行解就为一份试卷，所以本研究将一份试卷映射为1个染色体，组成试卷的各个试题映射为基因，基因的值直接用试题的ID表示，这样染色体的编码可表示为：(G1，G2，G3…，Gn)，其中 Gi(i=1～n，n 为试卷的总题目数)为试题的ID。编码时应将同一题型的试题放在一起，并保证每条染色体上的基因不重复，即每套试卷中不能出现重复试题。

试题的难度分为4档，本研究采用离散型随机变量的二项分布函数B(n，p)建立 1个由试卷的期望平均分P计算难度分布的模型。

离散型随机变量的二项分布函数B(n，p)：

其中，k=0，1，2，…，n，n 为整数，p＞0，q＞0，p+q=1。

2.2 适应度函数

在遗传算法中，以适应度大小来区分群体中个体的优劣。一般而言，适应值越大的个体越好，越容易被保留而繁衍下一代：适应值越小的个体越差，更容易被淘汰。适应值的选取是遗传算法设计的关键，它直接决定算法的优劣以及该组卷策略的科学性。本研究提出的自动组卷模型是基于知识点分布的，采用如下方法设定适应度函数F，F分别由 f1，f2和f33个子函数组成。

f1表示章节分数分布适应函数。 设 Ci、Xi、ei(i=1，2，…，m，m为章的数目)分别表示用户要求的各章应占的分数、实际生成试卷中各章所占的分数、用户允许各章的分数误差。生成的试卷满足用户关于内容分数分布要求的程度可以用式(2)值的大小来评价：

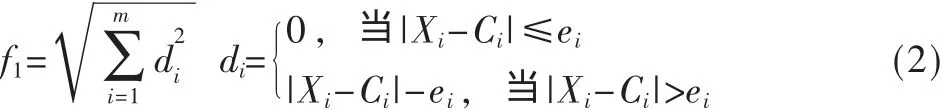
其中m为总章数，Xi为实际分配的分值，Ci为预期值，ei为允许误差。

式(2)采用方差来统计章节分数分布的偏差，而不用di的差的绝对值来表示，是因为f1是用来评价某份试卷对每一章的适应度的误差，只是简单地将误差值累加，不能充分表现该试卷每一章的偏差。

f2表示知识点的覆盖率和考核点类型的分配比例的适应值函数。本研究以考核点的覆盖率作为一项“软”约束条件，即考核点覆盖率越大。该试卷的适应度越大；同时根据命题的经验，如果一份试卷的考核点类型分布比例越接近5:3:2，那么该套试卷的命题比例越科学，其试卷的考后成绩越容易呈正态分布，故本研究将这2个参数也作为适应度函数之一：

其中n为本章总分数，a是考核点为重点的分值分配，b是考核点为次重点的分配分值，c是考核点为一般的分配分值，tc为该套试卷所占的不重复考核点数，tm为该门课程总考核点数。

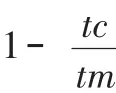
f3表示难度分布适应度函数。设 Ai、Si、ei(i=1，2，…，n，n为难度等级数)分别表示用户期望的每个难度等级应占的分数、实际试卷中各等级所占的分数、允许误差。生成的试卷满足用户关于难度分数分布要求的程度可以用式(4)值的大小来评价：

同理，该式的方差值越小，说明该试卷的难度分布越接近用户预期要求，适应度越好。

因此， 该试卷的总体适应度值 fmin=f1+f2+f3，fmin越小越好，是最小化问题。本研究采用如下方法将目标函数fmin转化为适应度函数 fmax：

因为指数比例既可以让非常好的个体保持多的复制机会，同时又限制了其复制数目以免其很快控制整个群体，提高了相近个体间的竞争，所以对上述适应度函数fmax采用如下指数比例变换方法转换为适应度函数F:

式中，β=0.06。

2.3 选择算子

2.4 交叉算子

将以上选出的个体进行两两随机配对，对每一对相互配对的个体采用有条件的“均匀交叉”，即2个配对个体的每一个基因座上的基因都按一定的交叉概率Pc和一定的条件进行交换，产生2个新个体[4]。

本研究对于交叉概率Pc的确定采用自适应的交叉概率。简单遗传算法中，交叉率是个常数，而实际上，优良的交叉率与遗传代数的关系较大。在迭代初期，交叉率选择得大一些可以造成足够的扰动，从而增强遗传算法的搜索能力，而在迭代后期，交叉率选得小一些可以避免破坏优良基因，从而加快收敛速度。因此，本研究选择的交叉概率是个能随着演化不断调整的函数，称为变交叉概率。交叉概率计算公式为：

Pc′是第 t代的交叉概率，Pc，max为最大交叉概率 ，取0.7，Pc，min是最小交叉概率，取值为 0.5，t为遗传代数，tmax是最大遗传代数。由于遗传代数t是变化的，所以交叉概率 Pc′是随代数 t而改变，除非 Pc′总是小于 Pmin。 每次交叉根据选择概率判定当前是否进行交叉，如果要交叉，则随机选出一对个体，在2个体中分别随机选择1个交叉位进行交叉。对2个配对个体的每一个基因座上的基因，先随机产生 1个 0～1的实数 r1，如果 r1＜Pc并且满足交换条件(即交换后个体的各个基因不重复)，则交换该基因座上的基因，否则不交换。

2.5 变异算子

由于普通的变异操作可能会使用户指定范围外的题目出现在染色体中，也会使各题型的题目数难以保证，本研究采用有条件的变异算子，即每个个体的每一个基因座上的基因都按一定的变异概率Pm在一定的范围内进行变异。

同样，本研究的变异概率也采用自适应变异概率。在简单遗传算法中，变异率是个常数。通常对于交叉率是常数的情况，群体的素质会趋于一致，这样就形成了近亲繁殖。群体基因的多样性变差不仅会减慢进化历程，也可能会导致进化停滞，过早收敛于局部最优解。因此，变异概率也能随着演化不断调整，由于概率表达式中含有遗传代数t，这个概率称为变动变异概率。变异概率计算公式为：

t为遗传代数，tmax为最大遗传代数，Pm，max为最大变异概率， 取值为 0.15，Pm，min是最小变异概率， 取值为0.01，λ为常数，取值为10。每次变异通过交叉概率判断当前是否变异。对于个体的每一个基因座上的基因，先随机产生 1个 0～1的实数 r1，如果 r1＜Pm，则根据一定的变异条件，即从备选题库中抽取一道同类型同分值的试题，同时保证该题不存在于该份试卷中，替换该基因座上的基因，否则不变异。

2.6 保存最优策略

为了保证优良个体在选择的过程中不被淘汰，对当前代进行了选择、交叉、变异操作产生新一代后，比较新一代的最好个体与其父代的最好个体的适应值，如果下降，则以父代最好个体替换新一代的最差个体。此策略可以保证迄今为止的最优个体不会被交叉、变异等遗传运算所破环，它是遗传算法收敛性的一个重要保证条件。

3 试验结果及分析

为了验证上述算法的可行性和有效性，利用一门计算机课程的题库进行研究，该题库中有1000道题，其题库结构如下。

(1)组卷10套，总分为100分，题型分配如表1所示。

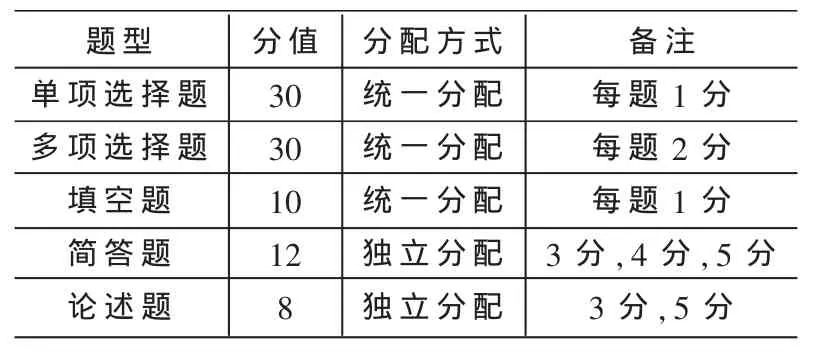
表1 题型分配表

(2)预期平均分为70分，经过计算得出预期难度分配为：

易:中等偏易:中等偏难:难=20:36:31:13

(3)要求考核点覆盖率达到70%以上，平均区分度在0.3～0.7之间，平均难度为中等偏易或中等偏难等级，考核点覆盖率(即重点:次重点:一般)接近 5:3:2。

(4)章节分值分布如表2所示。

表2 章节分值分布表

实验设置最大迭带代数GenMax=100，允许误差ei=2分，群体规模GenSize=100，结果各章的分布基本满足预期要求，难度和考核点类型比例基本接近正态分布，平均难度维持在第2～3等级之间，区分度在0.4～0.7之间，考核点覆盖率基本到达70%以上。目前该算法已在自学考试命题中试用，以便今后进一步推广。

[1]余胜泉，姚顾波，何克抗.通用试题库组卷策略算法[R].2000.

[2]曾一，冉忠，郭永林.试题库中自动组卷的算法及试卷测评策略[J].计算机工程与设计，2006(8):3024-3027.

[3]张爱文，樊红莲.自适应遗传算法用于自动组卷中的数学模型设计[J].哈尔滨理工大学学报，2006(11):18-20.

[4]MEHMET Y.Heuristic optimization methods for generating test from a question bank[M].MICAI 2007:Advances in ArtificialIntelligence， Springer Berlin/Heidelberg， 2007:1218-1229.