数字测频算法研究综述*

周晓青，李合生，陶荣辉，蔡英武

(中国工程物理研究院 电子工程研究所，四川 绵阳 621900)

在现代战争中，数字接收机是电子侦察系统的重要组成部分，它在广大的作战区域中准确、快速、全面地获得各种目标信息的作用巨大，其地位是不可取代的。它可以捕获、定位、分析和识别作战区域内的雷达辐射源，从而获取有用信息。其中电磁波的频率无疑是非常重要的一个参数，它反映了雷达的功能和用途、雷达的频率捷变频范围和谱宽，是信号分选和威胁识别的重要参数之一[1]。为了实时、准确地获得该参数，需要对载波频率进行瞬时测量。在20世纪五六十年代，瞬时测频技术IFM(Instantaneous Frequency Measurement)应运而生，瞬时测频主要分为模拟瞬时测频和数字瞬时测频两种。其中，模拟瞬时测频设备简单易于实现，但测频精确度不是很高，并且稳定性差，容易受环境的影响，该技术较早在工程中得到应用。数字瞬时测频具有稳定、精确度高、实时性好等优点。90年代中期以后，随着高速集成电路和数字算法的发展，数字瞬时测频DIFM(Digital Instantaneous Frequency Measurement)技术得到飞速的发展，并且有逐渐取代模拟瞬时测频的趋势。

数字瞬时测频即用数字信号处理的方法对信号的载频进行测量[2]。现代电子战争的主要特点为：(1)宽频带、大视场；(2)瞬时信号检测、测量和高速信号处理[1]。所以要求数字测频必须可以对大带宽的信号进行高速、高精度的测量。随着数字接收机的发展，对数字测频算法的研究也越来越多，这些方法各有优缺点，需要根据实际的应用场合选择使用。

本文主要按照算法所利用的信号的不同信息分量，对常用的一些算法进行了分类介绍，并给出了算法的基本思想以及目前比较常用的改进算法，对其中的直接计数法、相位推算法、频率推算法、傅里叶变换法及谱估计等方法进行了MATLAB仿真。总结了各算法的主要优缺点及适用范围，为设计者在工程实用中选择合适的算法提供帮助。

数字测频算法种类繁多，根据算法所利用的信号不同信息分量，数字测频算法分为：利用幅度信息的测频算法、利用相位信息的测频算法、利用频率信息的测频算法、利用功率谱信息的测频算法4类。下面将分别对这4类算法进行详细的分析研究。

1 利用幅度信息的测频算法

利用信号的幅度信息进行测频的典型算法为直接计数法[3-6](也称为过零计数法、过零检测法)，是通过计算一定数量的信号周期总共占有多长时间来推算信号频率。其原理框图如图1所示。

图1 直接计数法原理框图

设采样量化的时钟频率为fs，计算信号的n个半周期，即计算出一段信号极性变化n次的时间，总共的信号时间为m个时钟周期，则信号的周期和频率分别为：

由于计数结果总是整数，可能发生的最大误差为1个时钟周期，则可能的最大周期误差为2/nfs。或者用相对误差表述，测量信号周期和频率的相对误差均为1/m，当m较小时，计数法的测频误差较大，要提高m的数值，只能是提高采样频率和信号存在时间。

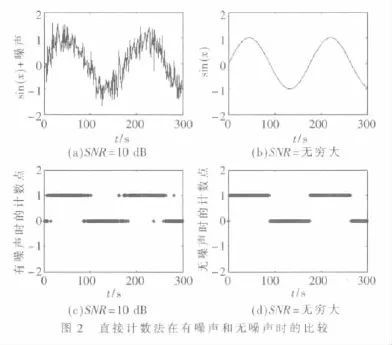
图2给出了直接计数法在有噪声和无噪声情况下的比较。图 2(a)、图2(c)分别为当信噪比等于 10 dB时的待测信号和直接计数法的计数点；图 2(b)和图2(d)分别为没有噪声时的待测信号和直接计数法的计数点。可以看出，当没有噪声时，计数点清晰可见，可完全满足频率计算的要求。但在信噪比为10 dB时，已经很难利用计数法对待测信号进行频率测量了。

为了进一步提高直接计数法的测频精度，参考文献[4]提出可以采用双门限整形的方式来降低在较低信噪比情况下的计数误差；参考文献[3]提出引入等效时钟来减小量化误差。由于直接计数法本身的抗噪声性能较差，所以这些方法虽然对算法有所改进，但性能仍有待进一步提高。

由以上分析可以看出，直接计数法的主要优点为：测频方法简单、运算量小、速度快、工程实现的体积小、重量轻。而其主要缺点：抗噪声性能差、测频精度较低，并且只能用于单载频测量。

2 利用相位信息的测频算法

在信号处理中，信息调制一般在信号的幅度、相位和频率上，在这三者中，将有用信息调制在幅度上的信号抗噪声性能一般是最差的，所以希望其能够从相位和频率中提取所需要的有用信息。

相位推算法[7-9]先把信号幅度转换为信号相位，再采用相位信息来计算频率值，如图3所示。实践证明，相位推算法可以得到较高的测量精度。

图3 相位推算法原理框图

假设被测量的信号具有如下形式：

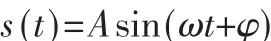
其中，A为信号幅度因子，ω为角频率，φ为相位，记录m个连续的采样点为：

式中，T为采样周期，经过一系列推算[7]，可得信号频率为：

其中 φi为：

式中，n为所使用的相位点数，fs为采样率。

用MATLAB对相位推算法进行了仿真，当采样频率fs=500 MHz、脉冲宽度 τ=2 μs、信噪比 SNR=10 dB、量化位数为 8 bit时，对 100 MHz～150 MHz的频率范围，每隔1 MHz进行1次测频，测得的频率误差如图4所示。

从仿真结果可以看出，测频误差最大不会超过3 kHz，达到了较高的测频精度。同时，相位推算法的测频实时性和抗噪声性能均较好。但缺点在于测频算法较为复杂，需要的硬件资源较多。

因此，相位推算法适用于对测频精度及实时性要求较高，且信号信噪比较高，有较多硬件资源的情况。

3 利用频率信息的测频算法

利用频率信息进行测频，包括在时域上和频域上进行测频两类算法。在时域上对频率进行推算的典型算法为频率推算法，而在频域上对频率进行推算的典型算法为傅里叶变换法。其中，对傅里叶变换法进行的研究较多，发展较快，目前有很多改进算法，同时也带动了对短时傅里叶变换以及小波变换在瞬时测频方面的研究。

3.1 频率推算法

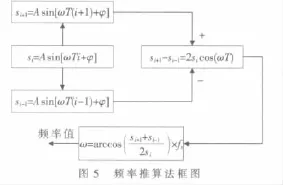
频率推算法[2，8-10]又称为曲线拟合法，是在假设信号为一个单一载频的情况下导出的一种算法，其原理框图如图5所示。

假设被测量的信号具有如下形式：

如果采样周期为T，则信号变成如下序列：

则可推出：

采样率fs=1/T，则信号频率与采样率之间的关系：

在已知采样率情况下，只需要3个采样点就可以得出信号的频率。但必须强调的是，这一算法的前提是信号必须是单一载频的。

如果要通过式(8)求取信号频率，必须满足2个条件：(1)si≠0，而且可以求取反余弦函数；(2)比较容易满足求取反余弦函数(可以利用CORDIC算法来求取)。第1个条件比较困难，在量化精度较低的情况下，较小的信号往往也会被量化为0，因此在工程上往往采用其改进算法，即用3点进行测频变为用多点进行测量[8]。

令 yi=si+1+si-1，xi=2si，K=cos(ωT)，有：

对于某一个被测频率，K=cos(ωT)是一个常数，则(9)式实际上是一个直线方程，直线的斜率为K。采用线性拟合，求一条直线，使这些点到直线的距离的平方和最小，这样就得到一个优化的K值，再用这个值去计算信号的频率。

本文对频率推算法进行了MATLAB仿真，当采样频率 fs=500 MHz、脉冲宽度 τ=2 μs、信噪比 SNR=10 dB、量化位数为 8 bit时，对 100 MHz～150 MHz的频率范围，每隔1 MHz进行1次测频，测得的频率误差结果如图6(a)所示； 当待测频率 f=200 MHz、脉冲宽度 τ=2 μs、信噪比SNR=10 dB、量化位数为 8 bit时，对 400 MHz～800 MHz的采样频率范围，每隔1 MHz进行1次测频，测得的频率误差结果如图6(b)所示。

从仿真结果可以看出，频率推算法的测频精度受采样频率的影响较大。在相同条件下，用频率推算法进行测频的最大误差不超过300 kHz，测频精度明显差于相位推算法，但仍具有工程应用价值，同时瞬时性较好。另外，由于频率推算法运算量大，所以在硬件实现时会耗费较多的硬件资源。

因此，频率推算法适用于对瞬时性及测频精度要求稍高，同时有较高的信噪比和充裕的硬件资源的场合。

3.2 傅里叶变换法

用傅里叶变换法来求解信号的频率是当前研究最多的一种算法。 傅里叶变换法[2，9，11-13]是将一段信号进行傅里叶变换，将时域信息转化为频域信息，在频域上的峰值点即对应该信号的频率。其测频精度依赖于采样点数的多少。

傅里叶变换法尤其适用于信噪比较低的情况，它的测频精度随着信噪比的降低并没有明显的降低。在时域上，当信噪比为0 dB时，傅里叶变换法的测频基本上还是正确的。此外，傅里叶变换法还可以对复杂信号进行频谱分析。本文对傅里叶变换法在不同信噪比的测评效果进行了仿真，当采样频率为10 MHz、FFT点数为2 048点、量化位数为8 bit时，仿真结果如图7所示。

图7(a)、(b)中信号都是频率为 1 MHz和2 MHz的多载频信号，图7(c)、(d)分别为其所对应的频谱。其中，图7(a)的信号叠加了噪声，信噪比为 0 dB，而图 7(b)的信号没有叠加任何噪声，信噪比为无穷大。从仿真结果可以看出，尽管信号叠加的噪声较大，但是在信号频谱上仍然可以较好地分辨出信号谱线，这说明傅里叶变换法具有很好的抗噪声性能。同时，傅里叶变换法还具有测量多载频信号频率的功能，图中可以清楚看到，1 MHz和2 MHz分别对应谱线。正是这些优点使得傅里叶变换法成为当今数字测频应用最为广泛的一种算法。

但是，傅里叶变换法也有非常明显的缺点：测频精度及瞬时性较差，其测频精度完全是依靠采样点数的多少，采样点数越多精度越高。这就要求要提高信号的采样率，而这一点对于高频信号来说非常困难，所以要求通过其他的方法来获得测频精度的提高。

但总体上来说，傅里叶变换法比较适用于信噪比低，对瞬时性和测频精度要求不太高，具有足够的硬件资源的场合。

4 利用功率谱信息的测频算法

谱估计法测频是通过求解信号的功率谱来确定信号的频率，它对多载频信号的分辨能力较强，对信噪比的要求较低，主要包括经典功率谱估计法和现代谱估计法。经典功率谱估计主要包括周期图法(又称直接法)和BT(Blackman-Tukey)法(又称为间接法或相关图法)。现代谱估计主要包括参数模型法(包括常用AR模型、最大熵法、最小熵法和线性预测法等)、最大似然法、自适应法、高阶谱估计等。下面将主要对经典谱估计中的周期图法和现代谱估计中的最大熵法进行分析。

4.1 周期图法

周期图法[2，14-17]是将平稳随机序列 x(n)的 N点观察数据xN(n)视为能量有限的信号，直接将离散信号xN(n)进行傅里叶变换来求取功率谱估计的。即首先由采样序列 x(0)，x(1)，…，x(N-1)，求得：

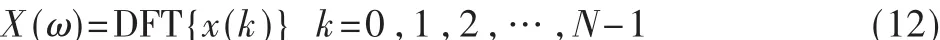
再由下式求得功率谱：

由于快速傅里叶变换(FFT)的提出，使DFT算法的运算量显著降低。因此，周期图法得到广泛应用。该方法的测频范围由采样率决定，测频精度和频率分辨率由采样率和采样序列长度决定。其频率分辨率为：fs/(2N)，fs为采样率，N为序列长度。在有限的信号样本长度下，为提高测频精度可使用内插法。

周期图法最大的优点在于可以对多载频信号进行测频，并且抗噪声性能较好。对信号x(n)=sin(2πf1n)+cos(2πf2n)+w(n)进 行 了 仿 真 ， 其 中 ，f1为 0.2 Hz，f2为0.3 Hz，w(n)为白噪声，信噪比为 0 dB，测频结果如图 8所示。

从图8中可以看出，在频率0.2 Hz和0.3 Hz处功率谱有2个峰值，说明信号中含有0.2 Hz和0.3 Hz的周期成分。并且，采样点数的增加并没有使周期图的方差减小，而是采样点数越多，周期图上的随机起伏反而越密集和剧烈。用有限长样本序列的FFT来表示随机序列的功率谱是一种近似算法，必然存在着误差。为了减小误差，使功率谱估计更加平滑，可以采用分段求平均的方法，即 Welch法[18]和 Bartlett法[19]，当前对 Welch法的研究更为广泛。参考文献[17]采用Welch算法对在4种窗函数情况下进行仿真，结合得到的结果，给出了选取合适的窗函数应注意的一般原则。

从以上分析可以看出，周期图法适用于需要测量多载频信号频率、且信噪比较低、对测频精度和测频实时性要求不高的情况。

4.2 最大熵法

由于周期图法功率谱估计需要对信号序列“截断”进行处理，所以必然存在误差。 最大熵功率谱估计[2，14-16，19-20]的目的是最大限度地保留截断后丢失的其他信号的信息，使估计谱的熵最大。

如果数据为 x(0)，x(1)，…，x(N-1)，其算法步骤为：

(1)计算预测误差功率的初始值P0和前、后向预测误差的初始值f0(n)。

并令 m=1。

(2)求反射系数。

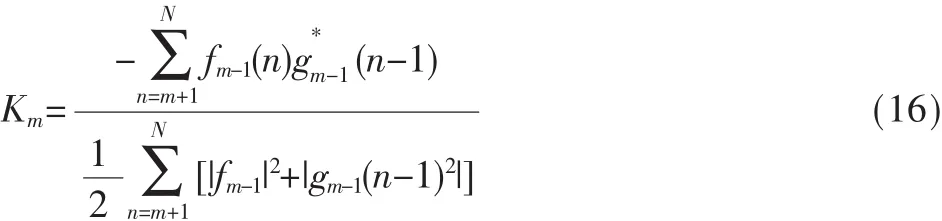
式中，*表示取共轭。

(3)计算前向预测滤波器系数。

(4)计算预测误差功率。

(5)计算滤波器输出

(6)令 m←m+1，并重复步骤(2)～步骤(5)，直到预测误差功率Pm不再明显变小。

最大熵法最大的优点在于可以较清晰地分辨相隔较近的两个信号，而这一点正是周期图法欠缺的，并且测频精度较好。对信号 x(n)=sin(2πf1t)+sin(2πf2t)+sin(2πf3t)+w(n)进行了最大熵法测频仿真，其中，f1为50 Hz、f2为 60 Hz、f3为 70 Hz、w(n)为白噪声、信噪比为 10 dB，仿真结果如图9所示。

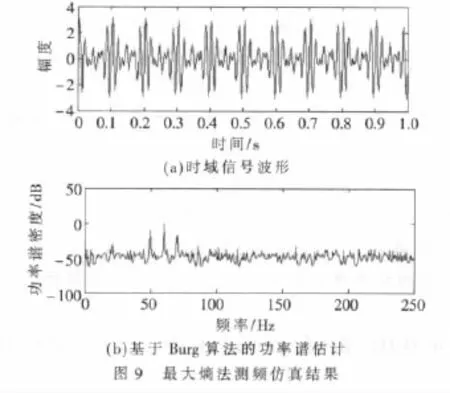
在图9中，可以非常清楚地分辨出3个频率，这是最大熵法相较于周期图法的优势所在，但是最大熵法仍然存在分辨率较低、频偏等问题。参考文献[20]提出了一种改进算法，使得其分辨率和运算速度有了一定的提高。参考文献[21]提出了一种修正算法，该方法在阶数估计时引入收敛因子，从而更为有效地估计了阶数，这种算法减小了频偏、提高了分辨率。

所以，最大熵法适用于需要测量频率相隔较近的多载频信号频率，且信噪比较低、对测频精度和测频实时性要求不高的情况。

通过以上的分析研究，对各种算法性能的比较如表1所示。

表1 各种算法性能比较

由表1可以得出：在信噪比非常差的情况下，可以优先考虑采用傅里叶变换法；在多载频信号测频时，可以考虑谱估计法；在对测频精度要求较高的场合可以优先考虑相位推算法；在对实时性要求较高，同时信号具有很高信噪比的情况下，可以采用直接计数法；在对实时性要求高，但信号的信噪比不太高时，可以采用相位推算法。

各种数字测频算法都有其不同的优缺点，需要在实际应用时根据不同情况加以选择使用。本文对这些算法加以总结，给出了各自的特点，其目的是为设计者在今后的实际工程应用中选择合适的算法提供参考。

[1]赵国庆.雷达对抗原理[M].西安：西安电子科技大学出版社，2005.

[2]王新春.高速宽带数字测频技术研究[D].西安：西安电子科技大学，2005.

[3]李相平.一种数字计数瞬时测频的方法研究[J].国外电子测量技术，2006，25(5)：7-8.

[4]胡来招.数字瞬时测频-直接计数法测频[J].电子对抗，2004(5)：44-49.

[5]魏钟记，刘峰，汪铭东.数字测频方法及实现[J].电子测量技术，2006，29(4)：28-29.

[6]张金刚，孟小芬，唐志凯，等.计数式瞬时测频精度分析[J].国外电子测量技术，2005(5)：10-11.

[7]喻旭伟.相位推算法瞬时测频研究[J].电子信息对抗技术，2007，22(6)：6-9.

[8]胡来招.数字瞬时测频-相位推算法测频[J].电子对抗，2005(3)：36-41.

[9]王伟旭.用相位推算法实现瞬时测频[D].成都：电子科技大学，2007.

[10]何伟.新型宽带数字接收机[D].成都：电子科技大学，2004.

[11]胡来招.数字瞬时测频-傅里叶变换法测频[J].电子对抗，2005(1)：42-47.

[12]陈文静.一种基于DFT快速频率检测的算法与实现[J].电子信息对抗技术，2006，21(3)：3-6.

[13]王峰.基于离散傅里叶变换的数字高速测频[J].数据采集与处理，2007，22：370-373.

[14]皇甫堪.现代数字信号处理[M].北京：电子工业出版社，2004.

[15]万建伟.信号处理仿真技术[M].长沙：国防科技大学出版社，2008.

[16]张贤达.现代信号处理[M].北京：清华大学出版社，2003.

[17]余训锋.改进周期图法功率谱估计中的窗函数仿真分析[J].计算机仿真，2008(3):111-114.

[18]WELCH P D.The use of fast fourier transform for the estimation of power spectra:a method based on time averaging over short，modified periodograms[J].IEEE Trans on Audio and Electroacoustics， 1967，15(2):70-73.

[19]BARTLETT M S.Properties of sufficiency and statistical tests[J].Proceedings of the Royal Society of London.Series A， Mathematicaland PhysicalSciences，1937，160(901):268-282.

[20]高勤.一种改进的 Burg算法[J].指挥技术学院学报，2000(4):81-84.

[21]罗丰.基于 Burg算法的短序列谱估计研究[J].电子科技大学学报，2005(10):724-728.