FFT滤波误差分析
杨 君, 吕镜清
(①装备指挥技术学院航天测控工程研究中心,北京 101416;②信息综合控制国家重点实验室,四川 成都 610036;③中国西南电子设备研究所,四川 成都 610036)
0 引言
FFT作为DFT的快速算法一直以来都是频谱分析的重要工具,由于DFT运算与复调制滤波器组运算的相似性[1-2],FFT的滤波功能也逐渐引起了重视,作为复调制滤波器组的快速算法近年来FFT在图像传输、信道化处理[3]、信号盲识别[4]等领域得到了应用。但是在实际工程设计中FFT的滤波输出常常与预期存在差异,主要表现在时域波形畸变、起始部分数据丢失等,这些差异可能造成后续数据处理产生严重误差,而对于FFT运算与滤波运算之间的具体差异相关文献并没有进一步论述,工程中往往只能通过反复调整其低通原型滤波器来接近预期效果,使得设计效率大大降低且滤波性能仍未得到根本保证,为此本文对FFT的滤波原理进行了推证,找出了存在滤波误差的原因,并给出了消除误差的方法。
1 FFT的滤波原理
根据卷积和的定义,一个时域离散信号 x(n)(长度为 L)通过一个FIR线性相位滤波器h(n)(阶数为M,长度为M+1)的计算过程如图1所示。
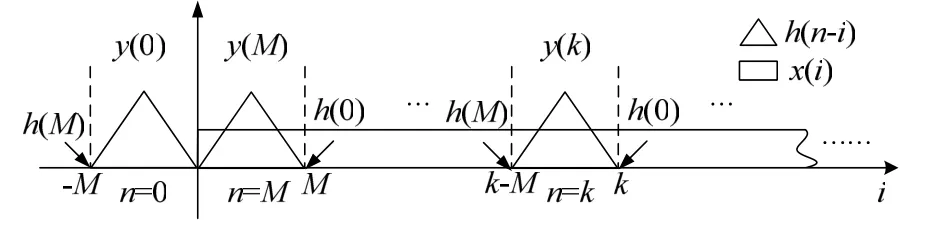
图1 滤波过程(y(n)为滤波输出)
如图1所示,第n时刻的滤波输出实际是x(n)及其之前的M个点(将这M+1个点定义为xn)与反向后的h(n)相乘再相加的结果,因此滤波结果完全可以等价表示为如下这种滑动相关的形式:

其中xn(i)=x(n-M+i)。在式(1)基础上定义一个新的函数:
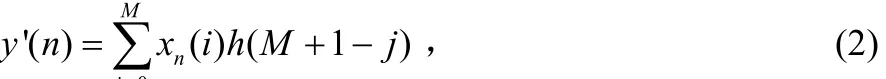
将求和式展开后比较式(1)和式(2),有如下结论:
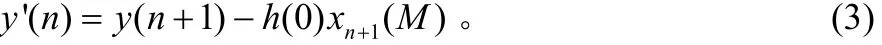
因此 y’(n)是 y(n+1)的近似,而近似程度取决于 h(0)和xn+1(M)的取值。也就是说,当h(0) xn+1(M)相对很小时,信号x(n)通过滤波器h(n)第n+1时刻的滤波输出近似等于进而有:
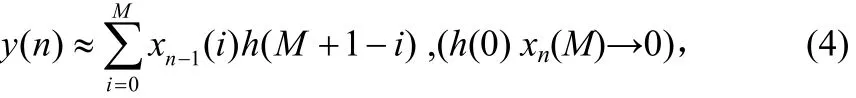
以M阶梳状滤波器[5](即系数全为1的滤波器)为低通原型,构造复调制滤波器组如下:
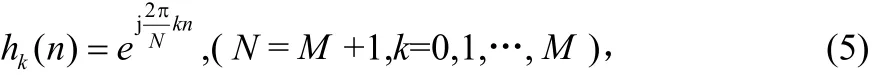
则根据式(4),信号x(n)通过该滤波器组时,第k个子信道的滤波输出为:
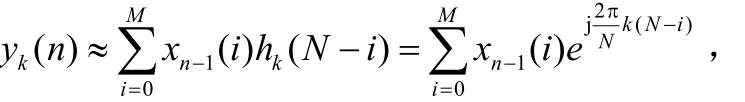

显然式(6)等号右边正是对xn-1做FFT的表达式。而前面定义xn(i)=x(n-M+i),因此FFT的滤波原理可以表述为:将第n-1时刻的输入数据及其之前的M个数据作FFT其结果近似等于以M阶梳状滤波器为低通原型的M信道(通道)复调制滤波器组第n时刻的滤波输出,而滤波误差为h(0)xn(M)即x(n)。
不难证明用 FFT实现低通原型为其它滤波器(记为h0(n),且阶数为M)的复调制滤波器组的表达式为:
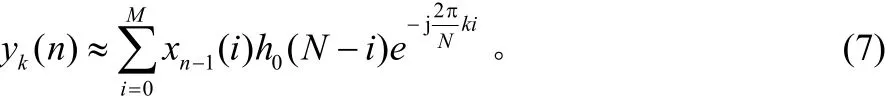
即先加窗再做FFT,所加的窗函数为反向移位后的低通原型h0(n),同时第n时刻滤波输出的误差为h0(0) xn(M)(即h0(0)x(n))。
2 频率响应误差
由于第n时刻FFT的滤波输出中缺少了h0(0) x(n)项(根据式(2)),相当于FFT等效的实现了以(n)为低通原型的复调制滤波器组,其中
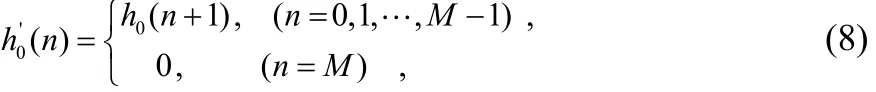
显然 h0(n) 的频率响应与(n)存在差异,下面进行详细论述。
2.1 误差分析
通常采用I类线性相位FIR滤波器(长度为奇数,系数偶对称)作为低通原型,因此h0(n)的频率响应为[2]:
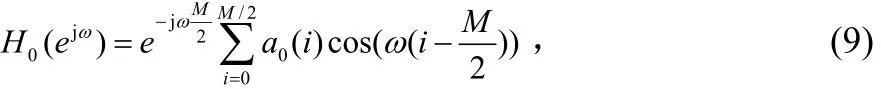
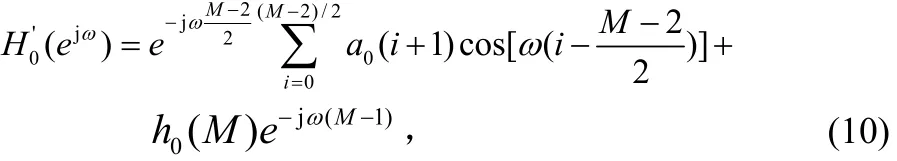
在式(10)中令:
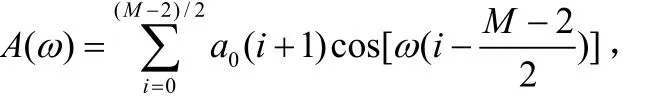
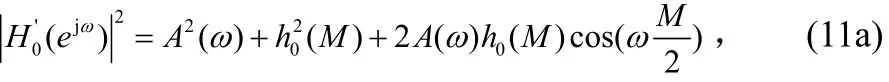
相频响应为:

其中()ωσω满足:
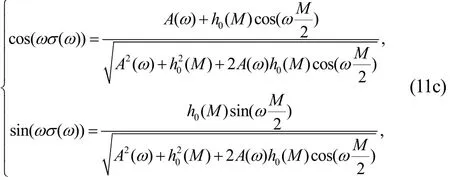
另一方面考查h0(n)的幅频、相频响应,根据式(9)有:

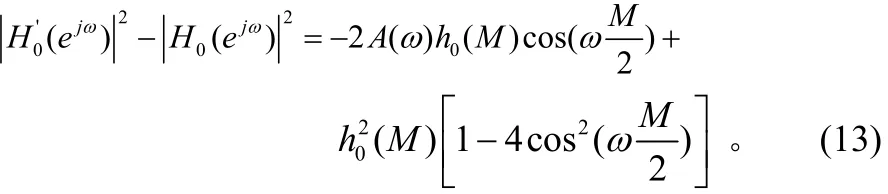
在通带内 A (ω)远大于 h0(M ),上式约等于 - 2A( ω )h0(M )·cos(ωM/2),此时如果的通带波纹与cos(ωM/2)有着相似的变化规律(比如用等波纹法设计出的h0(n) ),则会造成在取最大值时比大,在取最小值时比小,换句话说(n)增大了h0(n)的通带波纹,
其增大的幅度由 A (ω)在峰值频点上的取值以及 h0(M )的大小决定。另一方面在阻带内 A (ω)与 h0(M )相当,甚至更小,因此式(13)在阻带内取值会很小,比如用等波纹法设计出128阶的h0(n)其阻带衰减为-140 dB,而此时(n)的阻带衰减与其最大相差约6 dB,因此(n)相对于(n)在阻带上的变化是不明显的。
① 相频响应非线性;
② 可能造成通带波纹增大。
这里举例验证此结论。取归一化通带截止频率为 1/8,过渡带宽为1/80,在 Matlab的Filter Design & Analysis Tool中利用Equiripple法设计出不同阶数的低通滤波h0(n),其中最小阶数为16最大为1 024,阶数增加的步长取15,然后根据式(8)构造出相应的(n),对(n)通带内的频率响应进行误差分析。各频点的频率响应由DTFT(离散时间傅里叶变换)求得,归一化频率分辨率取10-5,各频点导数用斜率代替。仿真结果如图2所示。
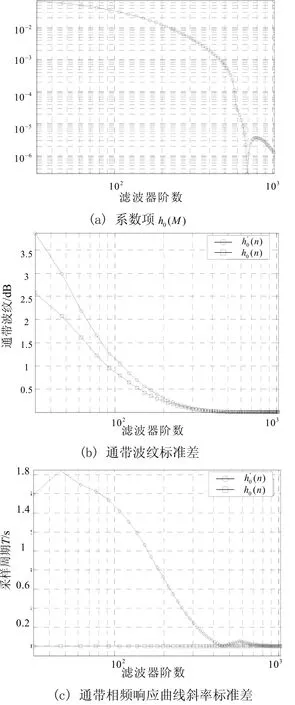
图2 ()n通带内的频率响应误差
仿真结果表明频率响应误差与 h0(M ) 存在密切关系。在阶数较小时 h0(M ) 较大,(n)通带内的频率响应误差较大。随着阶数的增加h0(n)本身性能提高导致 h0(M ) 逐渐减小,从而使得(n)通带内的频率响应误差逐渐减小。
2.2 误差影响
频率响应误差导致'
0()hn的滤波性能较 h0(n)有所下降,主要表现在:
①导致信号时域波形畸变;
②影响和信道滤波器的通带平坦度,降低和信道滤波器的滤波性能。
下面着重说明第二点。在图像传输以及信道化处理中经常需要将相邻的子信道滤波器相加来增加滤波带宽[6-7](将相加后得到滤波器称之为和信道滤波器),为了保证滤波质量,要求和信道滤波器通带平坦。假设以h0(n)为低通原型的复调制滤波器组满足和信道通带平坦的要求,当用FFT实现此滤波器组时其低通原型变为(n),其和信道滤波器的平坦度必然受到影响。下面举例说明。
取归一化通带截止频率为0.10375,过渡带宽为0.0425,在 Matlab的 Filter Design & Analysis Tool中利用Equiripple(等波纹法)设计出128阶低通滤波h0(n),根据式(8)得到(n),分别以h0(n)和(n)为低通原型构造8信道滤波器组,将第 2,3,4子信道滤波器合并,得到和信道滤波器通带平坦度对比如下。

图3 和信道通带对比
2.3 误差消除
根据式(11c)和式(12)可知,若 h0(M )为零则可以完全消除(n)的相频特性非线性以及幅频特性误差,因此在设计低通原型h0(n)时应注意使首末系数为零或尽量接近于零。利用窗函数法就可以很容易的设计出首末系数为零的低通滤波器。窗函数法设计出的低通滤波器系数具有如下特点:
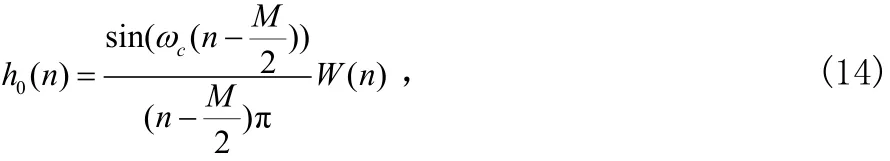
其中cω为通带截至频率,M为滤波器阶数,W(n)为选择的窗函数(如 Gaussion窗、Kaiser窗、Chebyshev窗等)。首末系数为:

显然只要ωcM/2为π的整数倍就可实现首末系数为零。当需要实现2D个信道的滤波器组时,低通原型的通带截至频率应设置为π/2D,此时ωcM/2=πM/4D ,因此只要阶数M为4D的整数倍就可实现首末系数为零。在设计滤波器时这一点是非常容易做到的。
事实上更为简单的方法是在已有滤波器的首末各补一个零,这样既不影响滤波器性能又消除了FFT时的频率响应误差。
3 相位超前现象
当h0(M)=0时可以避免频率响应误差,但是仍会产生相位超前现象。
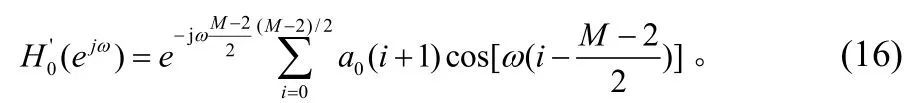
考查式(10),当h0(M)=0时'()hn的幅频响应为:
如果在用 FFT进行滤波运算时仍然认为群延迟为 M/2个采样点就会产生一个采样周期的误差。这个误差随采样周期的增大而增大,在一些场合中会影响数据处理精度,例如统一测控系统中的侧音测距,其利用收侧音相对于发侧音的传输延迟来推算出目标距离,公式可以简单的表示为R=Δt×C/2,其中R为目标距离,Δt为传输延时,C为光速3×108m/s,设中频欠采样频率为6.5 MHz,则算出的距离就会增加约23 m的误差。
另一种超前现象主要在事后数据处理时发生。在事后处理中由于数据都已获得因此N点FFT直接从前N个数据开始,等效于图1中从n=M,(N=M+1)开始向后滑动,滤波输出产生了M点的超前,这样起始M个点的滤波结果就会丢失,减去(M-2)/2个点的群延时,则最终造成起始的(M+2)/2个点数据丢失。而在实时处理时采样数据逐个进入数据缓冲区,而数据未到达的缓冲区数据位为零,等效于数据处理从图 1中n=0开始,因此实时处理不会出现此种超前现象。
两种超前现象都会造成滤波误差。对于第一种超前现象只需要在扣除滤波延时时用(M-2)/2代替M/2即可消除误差;对于第二种超前现象,在数据前补M个零即可等效于图 1中从n=0开始滤波,从而避免数据丢失。
4 结语
本文详细分析了 FFT运算与复调制滤波器组运算之间的差异,推导出了频率响应的误差项,并对该误差造成的滤波性能下降进行了仿真分析,针对误差产生原因提出了首末置零的简单方法以完全消除误差;另一方面文章分析指出了在实时及事后数据处理中 FFT相对于滤波器组存在的固有的相位超前现象,给出具体超前量和有效解决方法。文章为精确控制FFT的滤波性能及进一步提高其滤波质量提供了有效参考。
[1] Harris F J.Time Domain Signal Processing with the DFT,Ch.8 of Elliot,D.F.,Editor,Handbook of Digital Signal Engineering Applications[M].San Diego.CA:Academic Press,Inc,1987.
[2] 李素芝,万建伟.时域离散信号处理[M].长沙:国防科技大学出版社,2000:83-133.
[3] 王甲峰,葛晓碕.无盲区数字信道化实现方法[J].通信技术,2009,42(03):8-10.
[4] 杨伟超,张忠,丁群.低信噪比数字通信信号识别算法研究[J].通信技术,2009,42(01):68-71.
[5] Proakis J G, Manolakis D G.数字信号处理[M].方艳梅,刘永清译.北京:电子工业出版社,2007:367-372.
[6] Tsui J.宽带数字接收机[M].北京:电子工业出版社,2002:242-260.
[7] 陶然,张惠云,王越.多抽样率数字信号处理理论及其应用[M].北京:清华大学出版社,2008:122-130.

