考虑战场环境约束的多导弹协同任务规划

马培蓓， 纪 军， 范作娥

(海军航空工程学院，山东 烟台 264001)

0 引言

多导弹协同任务规划的目的是最大限度地利用威胁、禁/避飞区等战场环境信息，利用导弹间相互通信的数据链，以及集识别、通信、导航于一体的战术信息分配系统实现在飞行航迹上相互配合，协同有效地组织多枚导弹以完成共同任务为目标，为导弹设计出从出发点到目标点满足各项机动性能的协同飞行航迹，并通过获得更高的战效和对资源的充分利用，达到比单枚导弹更优的战术效果［1－3］。

当前协同航迹规划普遍研究的方法是通过选择合适的代价函数［4］预先规划好一组航迹，需要大量的计算时间;文献［5］提出一种基于几何航迹规划算法的参数最优化方法用以解决最优航迹问题;文献［6］提出一种非线性模型预测跟踪控制方法，在障碍回避、输入、状态约束条件下可用于解决航迹规划问题;文献［7］是以威胁源中心点为生长点构造威胁分布的Voronoi图，通过搜索最小代价路径实现多UCAV协同路径规划。

目前大部分研究都局限在无人机等单一飞行器的航迹规划问题上，对以多导弹为研究对象的协同航迹规划问题则少有涉及，另外现有的航迹规划方法大多没有充分考虑到战场环境，威胁均简单作为点目标处理，没有考虑到威胁的类型和强度差别以及禁/避飞区等面状区域对多飞行器协同航迹的影响，没有充分考虑多导弹协同航迹规划约束的复杂性，针对上述问题，本文重点研究了具有战场环境约束的多枚导弹的协同任务规划问题，包括战场环境建立、初始航迹生成、航迹动态优化处理和协同目标分配等。

1 问题的描述

多导弹协同任务规划的目的是为每枚导弹生成航路保证导弹能同时或按照一定的时间间隔到达各自的目标点，并且尽量回避威胁。这样生成的航路对每个单一的导弹来说，不一定是最优的，但对于整个导弹编队来说，一定是最优的或次优的。由于导弹的航迹规划需要处理非结构化、大范围、复杂的规划环境，这对许多传统的路径规划算法提出了挑战，因为过分冗长的时间往往失去了实际的可行性。为了满足协同作战的要求，需要同时规划多枚导弹到达多目标的航路并满足其在空间上和时间上的协同关系。

文献［8］中基于最短切线法的威胁规避算法进行预先规划。最短切线威胁规避算法，是指根据切线最短和协调次数最少的原则，在一定的假设条件下，从目标点开始，按照攻击方向的反方向依次逆推直至发射点，在此航路基础上进一步考虑威胁存在情况，按照修正后的航路走切线的思想，将处于威胁区域内的航路点调整为安全航路。图1和图2分别给出了威胁为5个的情况下，攻击角度λ＜0和攻击角度λ＞0的航迹规划的结果。

但文献［8］只研究了单枚导弹攻击同一个目标的多航路规划问题，这与多枚导弹的协同航路规划问题相比，虽然也需要生成多条不同的航路，但它们之间有着本质的区别。

1)单枚导弹多航路规划生成的各条航路的起始点和目标点都相同，但在多导弹协同航路规划中，不同导弹的起始点和目标点并不一定相同;

2)单枚导弹多航路规划算法一般对实时性不要求，但多导弹协同航路规划要求在线进行实时航路再规划;

3)单导弹多航路规划只要求生成在空间上较为离散的多条航路即可，但多导弹协同航路规划还需要满足各导弹之间的协同性要求，即要求导弹相互之间不能碰撞以及各导弹必须同时或依次到达目标。

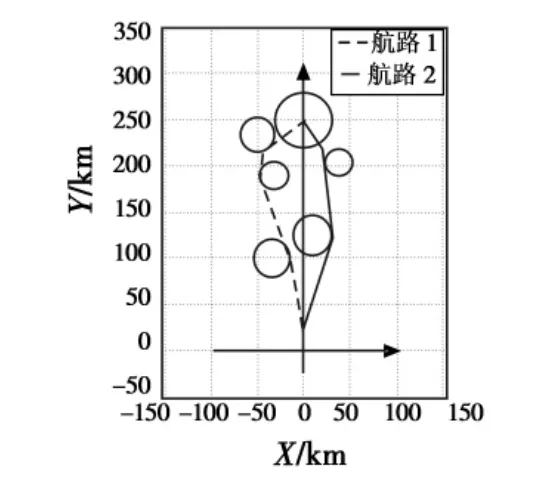
图1 λ＜0时仿真结果Fig.1 Simulation results when λ ＜0

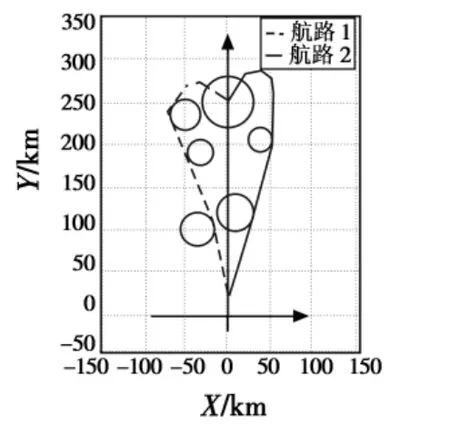
图2 λ＞0时仿真结果Fig.2 Simulation results when λ ＞0

2 多导弹协同航迹规划算法

多导弹协同系统实质是一个多动态的实体，各导弹之间通过数据链共享信息或任务完成一个共同的目标，但此目标大于每枚导弹的目标，即一枚导弹的航路最优不能代表多导弹协同系统的航路最优，有时为了提高整个系统的协同性，不得不牺牲个体的最优性。下面研究存在威胁和禁飞区的战场环境下多导弹协同航迹规划算法。

2.1 建立战场环境

导弹通常主要遭受两种类型的威胁:一是探测性威胁，另一种是杀伤性威胁。探测性威胁主要指各种普通对空雷达、预警机雷达等，其威胁度计算模型有多种，最常用的是根据雷达方程计算。

即认为威胁源对于威胁作用范围内的导弹的威胁度与导弹到威胁源距离的四次方成反比，如式(2)所示。

杀伤性威胁主要指各种防空导弹、高炮等。常用的计算方法如式(3)表示。

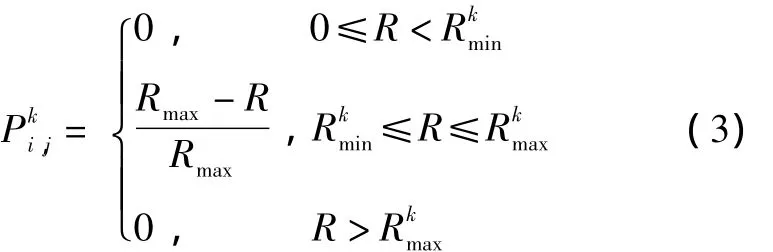
其中:(xi，yi，hi)为威胁源的位置;(xj，yj，hj)为导弹的位置;K为威胁源战技指标，是和导弹反射面积有关的系数;和分别为探测性威胁源的探测近界和远界;和分别为杀伤性威胁源的最小和最大杀伤距离;，为导弹与威胁源的距离。表1描述了典型的威胁及杀伤距离和威胁度。

表1 典型威胁Table 1 Typical threats

2.2 战场环境下V图的建立

由于战场环境中的威胁存在类型和强度的差别，在构造战场环境的V图形式化表达时，必须建立任意两个威胁体之间的等价关系，此时建立的V图已不是传统意义上基于欧氏距离的V图，称之为扩展V图(Extended Voronoi，EV)。基于扩展V图的基本原理和性质如下所示［9］。

性质1:设Wi，Wj是平面内两个威胁点，并且 Wj的威胁值是Wi的k倍，假设k＞1，则到Wj的距离是到Wi距离的k倍的点的轨迹是圆。

性质2:在局部空域内，若 Wi，Wj，Wk是平面内 3个威胁点，并且Wi的威胁值是Wj，Wk的k倍，且k＞1，而Wj，Wk的威胁值相等。

性质3:在局部空域内，若 Wi，Wj，Wk是平面内 3个威胁点，Wj，Wk的威胁值是 Wi的 k倍，且 k＞1，而Wj，Wk的威胁值相等。

遵循扩展V图的性质1、性质2和性质3，建立基于不同威胁的扩展V图，如图3所示。

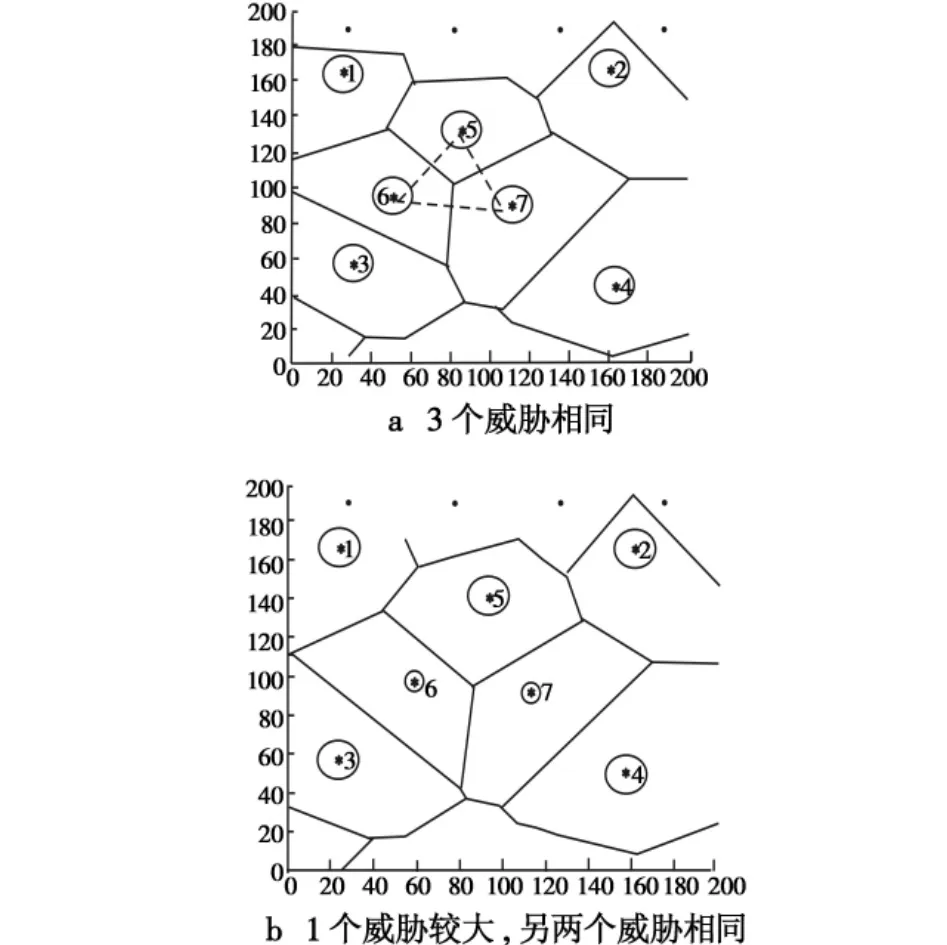
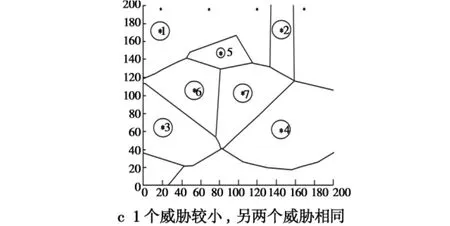
图3 不同类型威胁的扩展V图构造Fig.3 Extended Voronoi for different type of threats

在构造扩展V图时，禁飞区和避飞区作为面状生长目标处理，所生成的V图的边很可能非直线，而存在曲线的情形。本文仅考虑禁/避飞区的作用距离均为10000 m的情况，如图4所示。

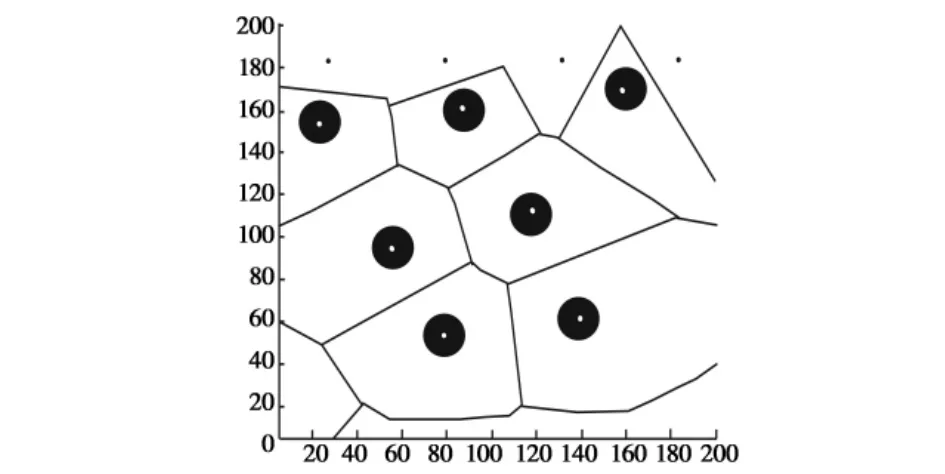
图4 仅包括禁/避飞区的扩展V图Fig.4 Extended Voronoi for no-fly zones

2.3 经典Dijkstra算法的改进和实现

Dijkstra算法是解决这种问题的最有效算法之一，其时间复杂性是O(n2)。经典的Dijkstra算法是用于求解从连通图中的一个顶点出发到图中其他所有顶点的最短航迹，并且也只给出了从起始点到其他各点的最短航迹的长度，而没有给出源点到其他各点的最短航迹所经过的中间点，本文求解的问题要求给出中间节点，因此对Dijkstra算法做了适当的修改。

第1点修改:Dijkstra算法的结束条件。

经典Dijkstra算法中，按航迹长度递增产生各顶点的最短航迹，求得从源点到所有顶点的最短航迹时，算法自动结束。而在修改后的Dijkstra算法中，每当求得一个顶点的航迹后，就判断该顶点是否为规划目标点，若是规划目标点就结束，否则继续。

第2点修改:把Dijkstra算法用于记录起始点到每一顶点的航迹长度的数组进行了扩充。

在经典Dijkstra算法中，算法结束时只给出源点到各顶点的最短航迹长度，具体源点到各顶点的最短航迹途中经过了哪些中间点，由于数据结构的原因，算法并没有保存。而对算法修改后，当搜索到目标点后，就可以利用前驱信息，向前追踪到规划的起始点，求得最短航迹的全部顶点编号，从而可以绘制出规划所得的航迹。通过上述思想改进的Dijkstra算法，结果得到一系列航迹控制点，可将它们保存在一个矩阵中。

实际上Dijkstra算法在执行过程中产生了以初始点s为根节点的一棵树，随着算法的执行，该树向四面八方延伸，直到达到节点为止，算法的时间复杂性为O(n2)。显然有些分支无益于最短航迹的求得，需要及早删去某些多余的分支，从而减少计算最短航迹的所需要的时间，进一步降低算法的复杂性。假设在V图中任意给定两点s和t，则需沿着方向不断寻找边和节点加入航迹队列。首先找出航迹长度的限定值;然后利用该限定值降低算法执行过程中产生的二叉树的规模;最后，由二叉树节点的标记可以计算出最短航迹及其长度。如果将此算法对与s关联的未考虑的边重新执行常数次，则可求得s与t之间更短的航迹，具体算法可参见文献［10］，此算法的时间复杂性为O(n)。

2.4 航迹缩短与平滑

导弹的初始航迹经过的航迹点过多，则导弹需要过度频繁地转弯。在导弹机动性能的限制条件下，需要进一步优化导弹飞行航迹，通过沿着初始航迹的方向缩短航迹长度，消除不必要的转弯点。

本文提出了基于视线的航迹缩短算法，具体算法步骤为:

1)在初始航迹的每个航迹段(Voronoi边)上增加若干个新的节点(节点的数量可以变化)，这里假定每条Voronoi边被分成10段，这些节点替代了之前围绕着威胁区和禁/避飞区的点，以此用以提供缩短航迹所需的更多的节点;

2)将导弹的位置点作为优化航迹的第一个节点，目标的位置点作为最后一个节点，直接将导弹节点与目标节点相连，连线称为视线;

3)检查产生的视线是否与威胁区或禁/避飞区有相交点，如果没有相交点，则此视线即成为一条新的航迹段;如果有交叉点，则将导弹节点与目标点的前一个节点相连，再次判断是否与威胁区或禁/避飞区有相交点;

4)上述过程不断重复，直到产生的视线不与威胁区或禁/避飞区有任何相交，则此视线相对应的最后一个节点又成为新的开始点。将新的开始点与目标点相连，遵循相同的原则进行判断，直到开始点与目标点相重合，则新的经过缩短的优化航迹产生。

航迹缩短前后的仿真结果如图5所示。

通过缩短航迹既可有效回避威胁，又可使飞行航迹缩短，有效节省燃料。但由于缩短的航迹仍然存在转角急剧变化的情况，不能满足导弹最小转弯半径的要求，因此要进一步研究航迹平滑的问题。

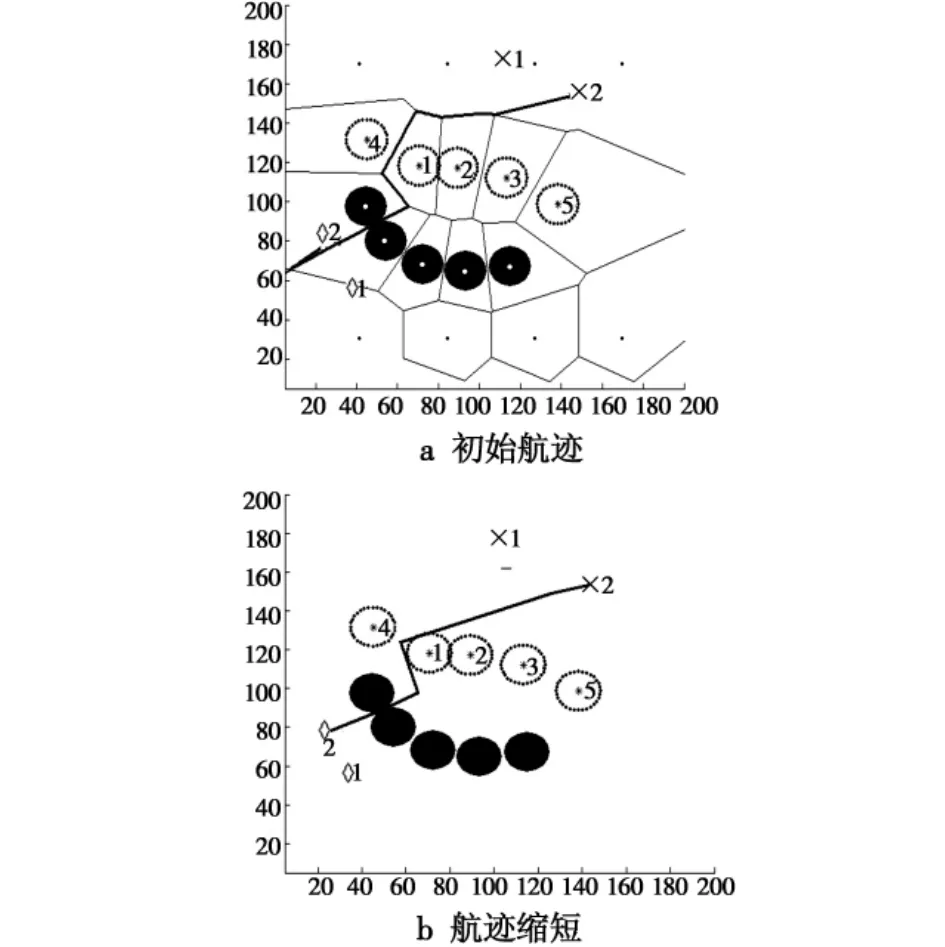
图5 航迹缩短的例子Fig.5 Example of path shortening

解决这一问题目前可以采用弹簧链路法、B样条平滑法等，上述方法虽然有效，但计算量相对较大。本文采用一种更为简单的方法，即在任意两条相关的直线段之间增加转弯段，转弯半径与导弹的过载与速度等侧向机动能力是密切相关的。取任意3个航路点Ai－1，Ai，Ai+1(不在同一条直线上)，航路段之间的航向转弯角为ψi，如图6所示。

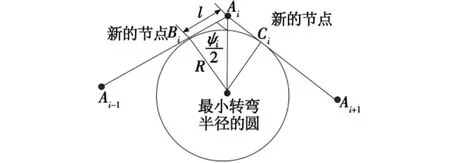
图6 路径平滑示意图Fig.6 Sketch of path smoothing

导弹航迹最初由直线段 Ai－1Ai切换到直线段AiAi+1，增加了转弯段之后，最小转弯半径圆与 Ai－1Ai相切于Bi点，与AiAi+1相切于Ci点。从图中可以看出，半径 R 分别与 Ai－1Ai，AiAi+1垂直，则:

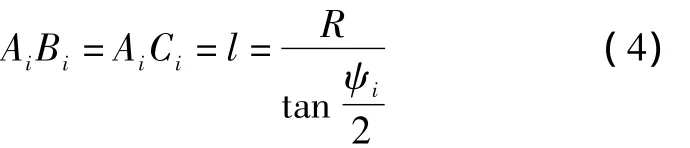
图7 航迹平滑的例子Fig.7 Example of path smoothing

通过航迹缩短与平滑的动态优化处理措施，导弹飞行航迹大大缩短，也满足了导弹最小转弯半径、速度、过载限制等战术指标要求。

3 协同目标分配

多枚导弹得到了缩短的、可飞的轨迹之后，还需要“进一步解决哪枚导弹攻击哪个目标”的问题，即协同目标分配问题。其目标是将不同位置、不同价值的目标分配给不同的导弹，尽力提高杀伤概率，避免重复攻击和遗漏，力求整体效益最大，代价最小。

通常将目标分配考虑为一类MMKP(Multi-dimensional，Multi-choice Knapsack Problem)问题，原理叙述如下:从集合I中选出一组满足所有问题约束的项，使其价值之和最大，其数学模型为［11］

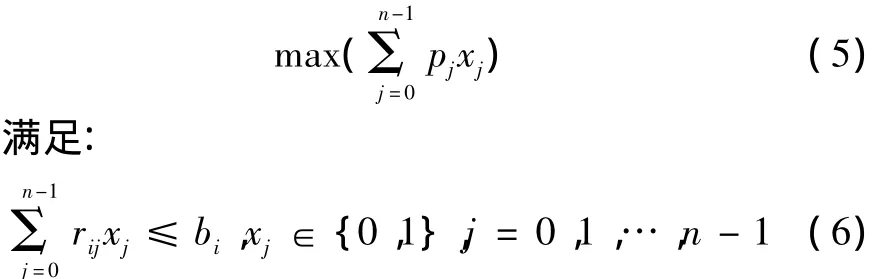
式中:n为项数且n＞1;pj为项j的价值且pj＞0;xj为对应项j的变量，且:

rij＞0为项j耗用资源i的量;bi为资源的总量;m为约束数，m＞1。一个定义完整的MMKP应该满足rij＜bi并且。而本文所研究的多导弹协同目标分配问题指的是m=1的一类特殊的0/1背包问题，即指派问题。指派问题是0/1背包问题的特例，其最优解具有这样的性质，若从系数矩阵C的一行(列)各元素中分别减去该行(列)的最小元素，得到新矩阵B，那么以B矩阵为系数矩阵求得的最优解和原系数矩阵求得的最优解相同。

本文采用匈牙利算法求解指派问题，为了降低问题的复杂性，确定以下约束条件:1)每个目标仅仅被攻击一次;2)每枚导弹仅仅攻击一个目标。

通过此约束确保每个目标都能被攻击到，防止遗漏，但同时也避免了被重复攻击，从而有效减小了任务分配可能的组合数量。

4 仿真结果分析

应用本节算法在 Intel Pentium Dual E22002.2 GHz，2 GB内存的PC上进行了仿真实验，运行环境为Windows XP，规划环境大小为200 km ×200 km，禁/避飞区和威胁区为模拟生成的圆形区域。

将某型号反舰导弹考虑为一个质心，不考虑重力影响，不考虑地球曲率影响。导弹初始速度v=340 m/s，最大法向(合成)过载为nmax≤2g，最大滚转角限制为导弹最小转弯半径，取平飞高度为200 m，导弹转向结束后为稳定航向所需走的最短距离为1 km，导弹最大拐弯角度为90°，假设目标静止。

导弹和目标的初始坐标分别为:导弹1(15.11 km，135.29 km);导弹 2(26.79 km，92.52 km);导弹 3(46.62 km，52.04 km);导弹 4(73.07 km，32.65 km);目标1(113.51 km，188.31 km)，战术价值为 60;目标 2(143.61 km，160.37 km)，战术价值为 80;目标 3(171.92 km，74.85 km)，战术价值为90;目标4(160.69 km，127.87 km)，战术价值为80。

共有4个禁飞区和4个威胁区，其位置坐标为:禁飞区1(66.33 km，150.11 km);禁飞区 2(104.97 km，123.88 km);禁飞区 3(82.95 km，82.83 km);禁飞区 4(135.52 km，60.03 km)，探测距离均为 10 km;威胁 1(122.94 km，86.82 km)，区域半径 30 km，威胁度 0.8;威胁2(68.89 km，111.99 km)，区域半径10 km，威胁度0.8;威胁 3(87.79 km，151.17 km)，区域半径 5 km ，威胁度 0.5;威胁 4(105.3 km，35.96 km)，区域半径 10 km，威胁度0.8。

在未考虑协同目标分配情况下，规划了16条最优飞行航迹，如图8所示。

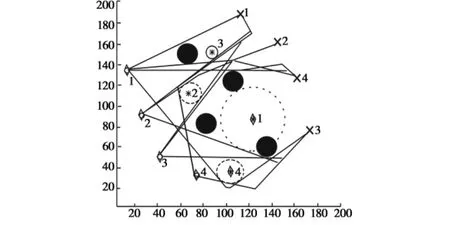
图8 4枚导弹攻击4个目标的最优航迹Fig.8 Optimal paths for four missiles attacking four targets

在考虑协同目标分配的情况下，协同航迹规划如图9所示，即由导弹1攻击目标2，导弹2攻击目标4，导弹3攻击目标1，导弹4攻击目标3，此时航迹总体代价最小。

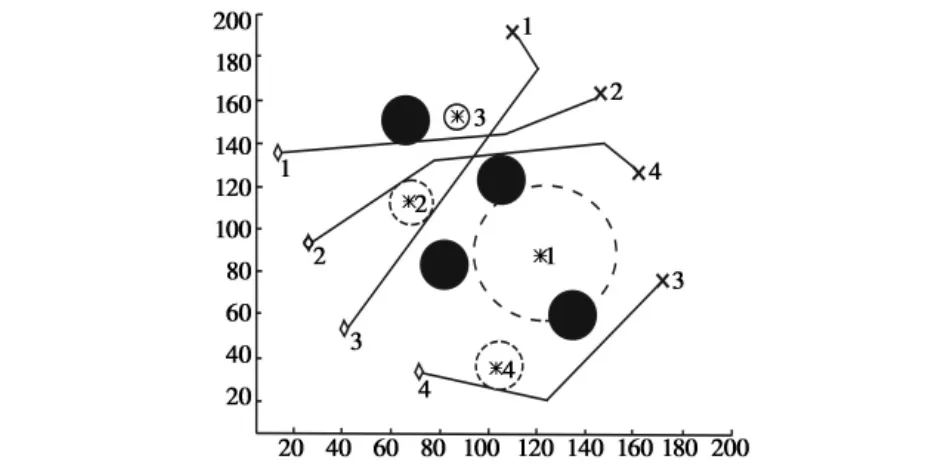
图9 协同分配后的最优航迹Fig.9 Optimal path after cooperative assignment

其终端航迹角度分别为 － 156°、132°、－ 66°和－114°。

5 结束语

本文针对具有战场环境约束多导弹协同任务规划问题展开研究。根据多导弹协同的特点，在研究了具体的战场环境模型，考虑了不同威胁作用距离和威胁度、威胁代价、距离代价基础上将禁/避飞区和威胁区作为面状生长目标建立了扩展Voronoi图并结合改进Dijkstra算法取得了代价最小的航迹;进一步采用基于视线的航迹缩短算法与航迹平滑算法，产生了满足导弹机动性能的平滑的可飞行航迹;最后采用基于MMKP的协同目标分配算法获得了总体代价最小的多导弹协同航迹。仿真结果表明了此算法的有效性。具有战场环境约束的多导弹协同任务规划算法可应用在多导弹协同攻击多目标，结合时间约束条件对目标实施饱和攻击等方面。

［1］BORTOFF S A.Path planning for UAVs［C］//The Proceedings of American Control Conf，2000:364-368.

［2］CHANDLER P R.Meir Pachter Complexity in UAV cooperative control［C］//The Proceedings of American Control Conf，2002:1831-1836.

［3］符小卫，高晓光.多架无人作战飞机协同作战的几个关键问题［J］.电光与控制，2003，10(3):19-22.

［4］BEARD R，MCLAIN T.Cooperative path planning for timing-critical missions［C］//Proceedings of the American Control Conference，Denver，Colorado，2003:296-301.

［5］YANG G，KAPILA V.Optimal path planning for unmanned air vehicles with kinematic and tactical constraints［C］//Proceedings of the 41st IEEE Conference on Decision and Control，(Las Vegas，NV)，2002:1301-1306.

［6］KIM H J，SHIM D H，SASTRY S.Nonlinear model predictive tracking control for rotorcraft-based unmanned aerial vehicles［C］//Proceedings of the American Control Conference，(Anchorage，AK)，2002:3576-3581.

［7］高晓光，符小卫，宋绍梅.多UCAV航迹规划研究［J］.系统工程理论与实践，2004(5):140-143.

［8］张友安，范作娥.反舰导弹航路规划与威胁规避算法［J］.吉林大学学报，2008，38(3):746-752.

［9］高晓光，杨有龙.基于不同威胁体的无人作战飞机初始路径规划［J］.航空学报，2003，24(5):435-438.

［10］周培德.计算几何—算法设计与分析［M］.3版.北京:清华大学出版社，2008.

［11］王乐.对解决背包问题的遗传禁忌搜索算法的研究［D］.郑州:郑州大学，2006.