超级紧组合中弱GPS信号跟踪算法
张敏虎, 任 章, 华春红
(北京航空航天大学自动化科学与电气工程学院,北京 100191)
0 引言
GPS接收机为了完成位置和速度的测量,必须对GPS信号进行码和载波的连续跟踪。传统的无辅助码和载波跟踪环必须跟踪卫星动态、接收机动态和本地时钟动态。因此,在中等动态条件下,采用二阶环路的传统接收机的带宽一般为12~18 Hz[1]。在高动态条件下,无辅助接收机必须采用三阶以上环路来削减动态,但是高阶环路设计复杂又存在稳定性问题[2-3]。
近年来,超级紧组合(深组合)得到了很大的进展[4-6]。其方法是使用滤波技术对INS的误差进行最优估计,同时使用校正后INS的位置、速度和加速度信息对码环、载波环进行辅助或直接闭合载波、码环跟踪回路,从而去除几乎所有的接收机和卫星动态,减小跟踪环路的等效带宽到3 Hz以下,增强了GPS接收机的动态性能和抗干扰能力[7]。预检测积分时间为20 ms深组合导航系统比普通接收机信噪比提高10 dB以上[8]。
超级紧组合系统能够进一步提高信噪比通过扩展预检测积分时间到20 ms以上,这就要求擦除每20 ms的GPS导航数据位引起的相位跳变,从而防止相关积分时间内的能量损失,提高估计精度。擦除可以在有辅助或先验知识的情况下进行,但是辅助数据必须被及时传输至接收机,这就必须增加成本;先验知识又因为不能确定何时广播导航数据改变,所以不可靠。因此本文提出一种基于能量估计的位合并数据擦除算法。通过仿真,验证了本算法可以在不需要数据位的先验知识和辅助的情况下,能有效地克服导航数据信息影响,提高超级紧组合系统的弱信号跟踪能力和精度。
1 超级紧组合结构
基于软件的超级紧组合GPS/INS导航系统见图1。系统采用一个卡尔曼滤波器代替了传统接收机的跟踪环路。GPS信号经下变频采样与本地产生的码和载波信号进行相关处理,经过相关累加后同向I和正交Q通道输出表达为[9]
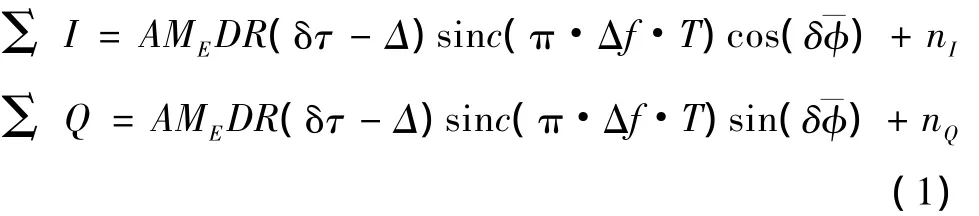
其中:ME为一个采样间隔内的采样数;A为信号幅度;D为导航数据(1或-1);R(·)为码自相关函数;δτ为码相位误差;Δ为超前、滞后码间隔;Δf为多普勒频率误差;T为预检测积分时间为平均载波相位差;nI和nQ为零均值方差独立的白噪声。最后,平均相位误差被进一步表达为[10]
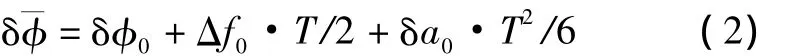
式中:“0”表示积分间隔开始时的误差;δa为频率变化率误差(相位加速度)。
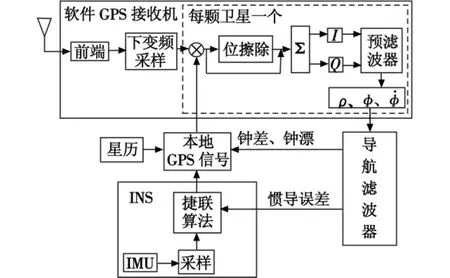
图1 超级紧组合INS/GPS结构Fig.1 Ultra-tight integrated INS/GPS architecture
同向和正交通道输出然后被送到预滤波器估计码相位差、多普勒频率误差和频率变化率误差。这些误差不去反馈追踪环路,而是直接与下一次积分时估计的误差进行卡尔曼滤波。所以,每一颗被跟踪的卫星的间隔可以是不相关的,即可以根据不同的卫星信噪比采用不同的预滤波速率。最后,所有预滤波器的估计输出被送入导航滤波器用来估计惯导误差状态和钟差与钟漂。校正后的惯导输出和时钟信息与星历数据一起被用于产生本地的复制码和载波信号从而构成闭环负反馈系统。
在目前分析中,预滤波器状态量选取为
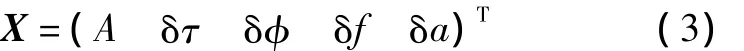
状态模型有如下形式[10]:

式中:C/N0为输入信号载噪比,系统导航滤波器的状态与量测模型见文献[4]。
分析式(6)、式(7)可知,在输入信号载噪比一定的情况下,预滤波器的量测噪声方差由预检测积分时间确定。随着预检测积分时间的增加,量测噪声随之减小,预滤波器估计更加准确。但是式(1)中的D是GPS的载波上采用BPSK方式调制的50 Hz的导航电文,所以I和Q的极性有可能20 ms翻转一次[11]。因此,一般的导航组合系统预检测积分时间不经数据擦除不能超过20 ms。如果采用图1中的位擦除后相加,则可以用更长的预检测积分时间。同时,又从式(1)可知积分后信号的能量损失估计的频率差(惯导估计速度差)有关,损失量可用sinc(π·Δf·T)函数来衡量。既然GPS的L1频率为1575.42 MHz,则辅助速度误差为0.3 m/s的信号可以导致最大为1.5 Hz的多普勒频率误差。而0.3 m/s的速度误差在1 s内一般校准后的普通MEMS惯导可以达到[9]。对于1.5 Hz的多普勒频率误差0.1 s的预检测积分时间可以导致0.32 dB的能量损失,这是一个可以接受的值。如果将积分时间扩展至300 ms,则能量损失为3 dB,这将极大地削弱信号幅值,所以积分时间又不易过长。本文中的相关积分时间选为100 ms。
2 数据擦除算法
擦除的算法由两步计算组成。对于第一步,采用0.1 s的预检测积分时间,在此段时间内导航数据可能导致5次相位转换。因为在捕获程序中已知导航数据跳变点,跟踪从此点开始。所以可以将每20 ms的数据输出转换成一个导航数据位,将5个这样的排列储存起来。原始的信号极性可能的组合方式共有25即32种排列方式。但是带有相反符号位的组合具有相同的能量例如:{-1 -1111}和{11 -1 -1-1}。因此最大能量位组合的选择是不具有相同能量位的组合,这样经过合并的数据选择可能方式降至24即16种可能。能量计算16种导航数据位合并通过下面的矩阵计算来解决。将5个I和Q数据输出记为ik,qk,k=1,…,5,它们为20 ms的导航数据位内部能量积累;同时用H阵来表示包含16种数据可能方式的矩阵,H阵的每一行表示一种可能的数据位组合方式。
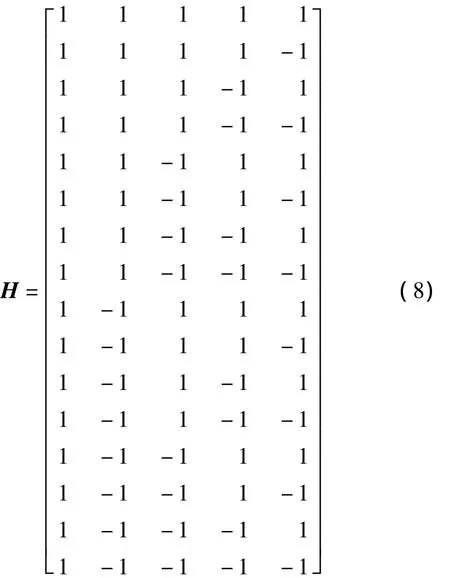
用I和Q表示矩阵相乘后的输出,对于所有的输出I和Q共有16个值。


第二步,将第一步求得的16个I和Q值分别平方相加求得100 ms间隔的信号能量。
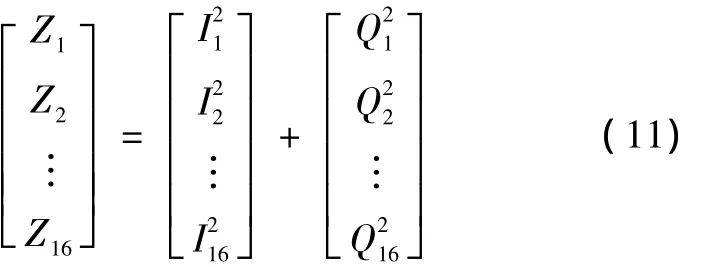
通过找出所求信号能量的最大值即认为是最可能的数据组合方式。
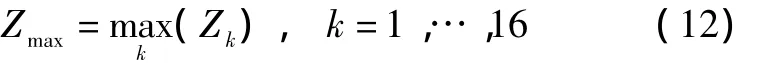
此时求得的最可能的选择为
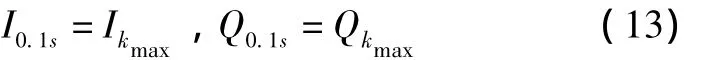
这里的数据擦除算法的目的不是去正确的解码导航信息,而是为了能够在一定的错误位信息的情况下积累足够的能量从而保持跟踪环的连续跟踪。
3 仿真验证
仿真实验分为擦除算法和动态性能两部分,所用的数据均采用Matlab仿真产生。
3.1 擦除算法仿真
经下变频数字化后的GPS中频输入信号可以表示为

其中:A为信号幅度;C(·)为C/A码;D(t)为数据码;n(t)为白噪声;τ为码延迟;fIF为载波中频频率;φ为载波相位;fd为输入信号多普勒频移。在仿真中,采用中频1.25 MHz,采样频率为5 MHz的仿真信号。生成仿真数据的噪声通常用高斯分布,信号的幅值是基于噪声基础上生成的,假设输入带宽为2 M,则信号的幅度可以表示为[11]

此时,信噪比(SNR)与载噪比相差63 dB。产生载噪比为17 dB-Hz的中频信号100 ms。分别设定导航数据位为{111 -1 -1}和{-11 -1 -11}。经过采用本文的方法估计,其能量幅值如图2所示,其能量最大在第4和第10个位置,对应的估计序列为{111 -1 -1}和{1 -111 -1}。分别对同样的序列在载噪比为16 dB-Hz和26 dB-Hz下测试100次,测试结果为16 dB-Hz下的误判别次数为3次,26 dB-Hz下所有的测试均正确。
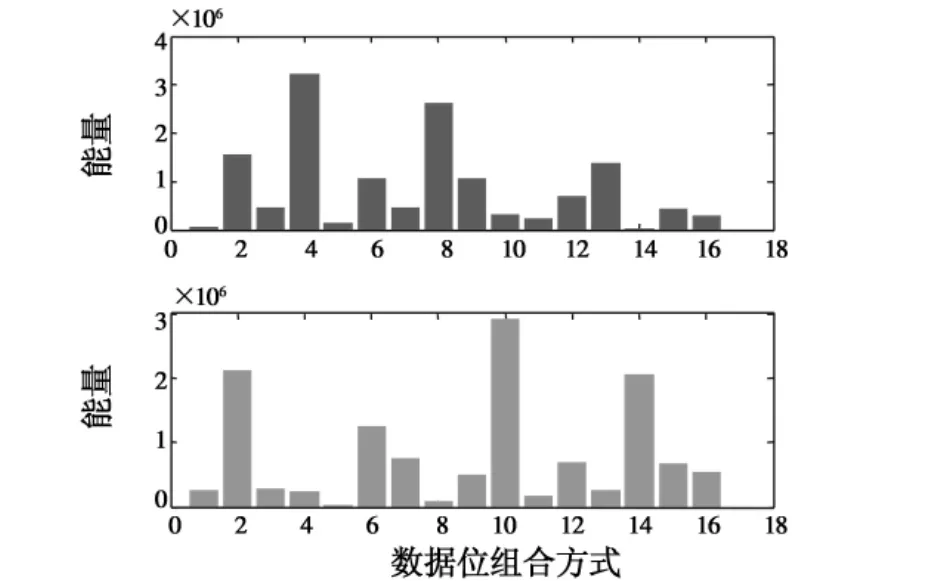
图2 估计数据位组合能量Fig.2 Energy of possible data bit estimation
3.2 动态性能仿真
在动态仿真中,采用 UTC时间为2009-08-01T10∶09的yuma星历数据产生可见星信息用于仿真。在这段时间内,如果测试位置在北京(北纬39°54',东经 116°23'),则仰角在 15°以上可见星数目为8 颗,PRN 码分别为 7,8,11,13,17,20,23 和 25。分别对各颗可见星设定信噪比见表1。
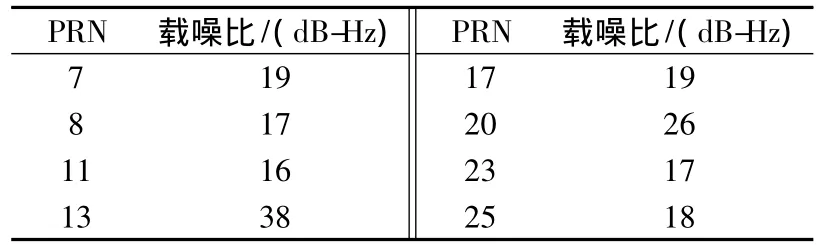
表1 卫星载噪比Table 1 Carrier-to-noise ratio of satellite
采用惯导的陀螺随机漂移为1(°)/h,相关时间为100 s,加速度计零偏为5 mg,相关时间为300 s,采样频率为100 Hz。恒温型晶振OCXO的频率和相位的随机摆动强度值[12]分别为 Sf=5 × 10-21s和 Sg=5.9 ×10-20s-1。先用轨迹发生器产生300 s的飞行轨迹,根据轨迹和卫星位置、速度计算相应的码延迟时间和多普勒频移,加入相应的噪声即为GPS中频输入信号。
在仿真开始,假设所有可见卫星都已经捕获,初始导航数据跳变位置通过捕获算法已确定。GPS中频信号的初始相位差假设为45°,飞行轨迹如图3所示。
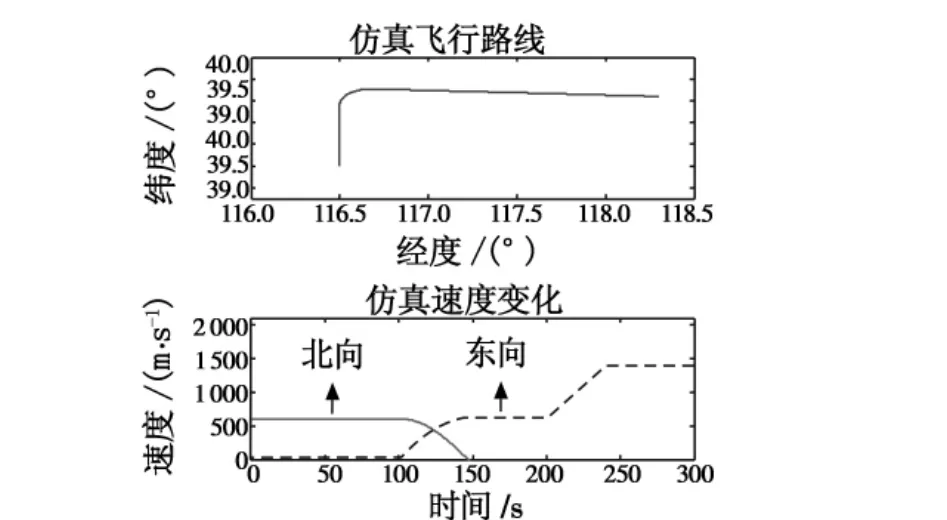
图3 仿真飞行轨迹Fig.3 Simulation flight trajectory
在飞行中100~150 s有一次北向东的90°转弯,200~240 s有2g的加速过程。
分别采用预检测积分时间20 ms和本文所擦除数据后的100 ms进行飞行测试,最低信噪比的11号卫星用20 ms预检测积分时间不能进行连续跟踪,而采用100 ms预检测积分时间却可以连续追踪。信噪比最高的13号卫星两种预检测积分时间都可以连续跟踪。相位估计误差如图4和图5所示。

图4 20 ms积分时间相位估计误差Fig.4 Phase estimation error for 20 ms of integration

图5 100 ms积分时间相位估计误差Fig.5 Phase estimation error for 100 ms of integration
从图中可以看出,对于同样信噪比的PRN13号卫星采用长的预检测积分时间可以比短的预检测积分时间获得更高的估计精度,100 ms预检测积分时间的估计精度在0.05周以内,20 ms预检测积分时间的估计精度却到了0.2周以上。而对于20 ms预检测积分时间不能跟踪的PRN11号卫星,用扩展到100 ms的方法可以稳定的跟踪,其误差也在1周以内。这说明了采用本文所述方法的有效性。最后,用本文所述方法扩展预检测积分时间后,超级紧组合导航系统的位置跟踪误差如图6所示,其误差在5 m以内。


图6 飞行位置误差Fig.6 Flight position error
4 结论
针对高动态弱GPS信号的跟踪问题,本文采用一种导航数据位擦除方法,通过此方法可将超级紧组合导航系统的预检测积分时间扩展到20 ms以上,这就可以有效地减少噪声的影响,获得更加准确的跟踪。通过仿真验证了采用本方法的超级紧组合导航系统能对载噪比为16 dB-Hz的11号卫星的码和载波连续跟踪。
[1]PETOVELLO M G,O'DRISCOLL C,LACHAPELLE G.Carrier phase tracking of weak signals using different receiver architectures[C]//ION NTM 2008 Conference,San Diego,CA,2008:1-11.
[2]吕艳梅,李小民,孙江生.高动态环境的GPS信号接收及其算法研究[J].电光与控制,2006,13(4):24-27.
[3]RAVINDRA B,WANG Jinling.Analysis of INS derived Doppler effects on carrier tracking loop[J].Navigation,2005,58(3):493-507.
[4]OHLMEYER E J.Analysis of an ultra-tightly coupled GPS/INS system in jamming[C]//IEEE/ION PLANS 2006,Fairfax VA:US Institute of Navigation,Inc 2006:44-53.
[5]RAVINDRA B,WANG Jinling.Ultra-tight GPS/INS/PL integration:a system concept and performance analysis[J].GPS Solut,2009,13:75-82.
[6]PETOVELLO M G,SUN D,LACHAPELLE G,et al.Performance analysis of an ultra-tightly integrated GPS and reduced IMU system[C]//ION GNSS 2007,Fort Worth TX,2007:1-8.
[7]鲁浩,位晓峰,庞秀枝.惯性技术在精确制导武器中的应用与发展[J].电光与控制,2007,14(3):45-47.
[8]LASHLEV M,BEVLY D M,HUNG J Y.Impact of carrier to noise power density,platform dynamics,and IMU quality on deeply integrated navigation[C]//Position,Location and Navigation Symposium,2008 IEEE/ION,2008:9-16.
[9]GAO Guojiang,LACHAPELLE G.A novel architecture for ultra-tight HSGPS-INS integration[J].Journal of Global Positioning Systems,2008,7(1):46-61.
[10]PETOVELLO M G,LACHAPELLE G.Comparison of vector-based software receiver implementations with application to ultra-tight GPS/INS integration[C]//ION GNSS 2006,Fort Worth TX,2006:1-10.
[11]JAMES B Y T.Fundamentals global positioning system receivers a software approach edition[M].2nd ed.New York:Wiley,2007.
[12]张欣.弱信号全球导航卫星系统接收机[M].北京:国防工业出版社,2008.

