空空导弹目标截获概率研究

李 峰， 王新龙， 王起飞

(1.北京航空航天大学宇航学院，北京 100191;2.中国空空导弹研究院，河南 洛阳 471009)

0 引言

中、末制导交接班时，空空导弹雷达导引头成功截获目标是导弹最终命中目标的重要前提［1－2］。

导弹对目标的截获性能可用目标截获概率来描述。导引头目标截获概率包括距离截获概率、速度截获概率、角度截获概率。在上述3个因素中，对导弹末制导截获概率影响最大的是角度截获概率［3－4］。为了保证角度截获，必须把导引头位标器预定到计算出的目标视线方向上。然而，工程中存在着理论上无法确定的各种误差因素会造成位标器指向与实际的目标方向之间的不一致，这种不一致被称为导引头指向误差［5］。在对截获概率的研究中，许多文献围绕着近、中程空空导弹惯性+指令修正中制导的角度截获问题，对载机雷达的测量误差、初始对准误差和导弹惯性元器件误差等对导引头指向误差的影响进行了分析［1－7］。

当前，捷联惯性/卫星组合导航已成为AIM-120D、流星等新一代中远程空空导弹普遍采用的导航方式。因此，具体分析空空导弹采用捷联惯性/卫星组合导航时对目标截获概率的影响具有重要理论意义及工程应用价值。为此，本文以中远程空空导弹为对象，系统分析了目标位置测量误差、导弹位置、姿态测量误差对导引头目标截获概率的影响。

1 速度截获概率

导弹的速度截获概率是指导引头雷达对目标多普勒信号的捕获概率。影响速度截获概率的因素主要有:1)目标回波多普勒频率落入接收机多普勒滤波器频带内的概率Pfd;2)在回波落入滤波器的条件下导引头接收机正确检测到目标的概率Pd。

导弹的速度截获概率Pv为

在整个中制导过程中，导引头的截获系统根据导弹和目标的接近速度确定末制导开始时导弹与目标间信号传输的多普勒频移，以便为速度跟踪系统的滤波器进行频率定位，保证使目标回波信号落入滤波器通带。而由于多普勒频移是根据导航系统解算出的导弹-目标接近速度而得到的，所以与实际频移之间存在误差。目标落入导引头雷达滤波器组内的概率Pfd服从瑞利分布［7］:

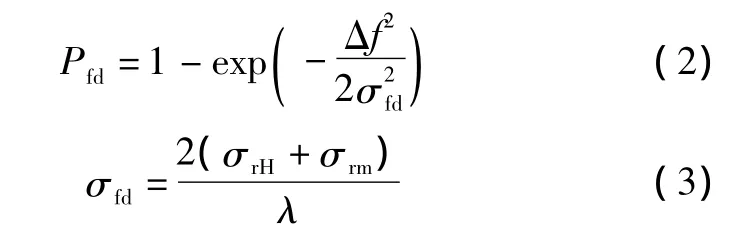
式中:Δf为导引头雷达滤波器组的频宽;σrH为机载雷达的测速精度;σrm为弹载惯导的测速精度;λ为雷达导引头的工作波长。

设导引头雷达滤波器组的频宽为6 kHz，机载雷达的测速精度为10 m/s，弹载惯性导航系统的测速精度为5 m/s，雷达导引头的工作波长为0.03 m，根据式(2)、式(3)计算得到 Pfd≈1。

导引头正确检测到目标的概率是信噪比SNR的函数。假设目标雷达截面积的起伏模型是施威林Ⅰ型，则检测概率为［8］

设虚警概率为10－8，信噪比为10 dB，积累脉冲数为 50，根据式(4)得到 Pd=0.92。

将式(2)和式(4)代入式(1)得到导弹的速度截获概率为 Pv=0.92。

2 角度截获概率

2.1 导引头指向误差模型

定义导引头坐标系如图1所示，图中:Oxbybzb表示导弹本体坐标系;Oxsyszs表示导引头视线坐标系;Oxs轴为导引头位标器指向;θs，ψs分别为导引头坐标系相对于弹体坐标系的俯仰角和方位角。

图1 导引头坐标系Fig.1 Seeker coordinate systems

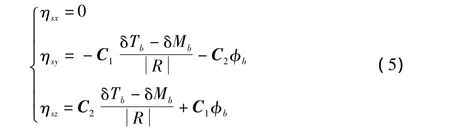
式中:C1= ［－ sinθscosψscosθssinθssinψs］;C2=［sinψs0 cosψs］;δTb表示目标的位置测量误差;δMb表示导弹的位置测量误差;φ表示导弹的姿态误差角;R表示导弹与目标的距离;下标b，s分别表示导弹本体坐标系和导引头坐标系。

从式(5)可以看出，影响导引头指向误差的主要误差源包括:雷达测量误差、初始对准误差和惯性元器件误差等。指向误差与这3个误差源的关系见图2。从图2中可以看出，雷达测量误差产生了目标位置测量误差;初始对准误差与陀螺仪测量误差产生了导弹姿态的测量误差;这两种误差又与加速度计的测量误差一起产生了导弹的位置测量误差。目标位置测量误差与导弹的位置、姿态测量误差共同组成了导引头指向误差。

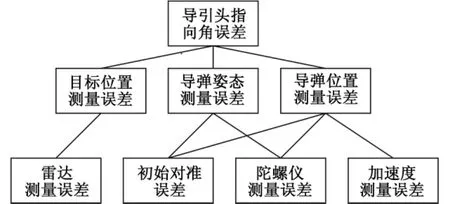
图2 导引头指向误差的分解Fig.2 Disassembling of the pointing-angle error of seeker

2.2 雷达测量误差对指向误差的影响

在导弹的中制导飞行过程中，载机雷达测量并计算的目标运动信息，此信息通过数据链发送给导弹。雷达测量目标位置的误差会引起导弹－目标视线角误差，从而使导引头的指向偏离目标实际的方向。

雷达测量目标位置通常用方位、俯仰和斜距3个量来描述。将雷达坐标系中的目标位置矢量转换到导航坐标系，得到载机与目标的相对位置矢量为

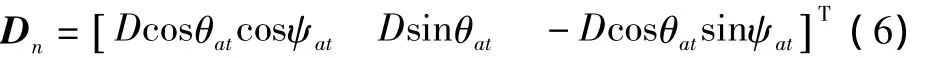
式中:D表示载机与目标的距离;θat表示目标相对于载机的俯仰角;ψat表示目标相对于载机的方位角;下标n表示导航坐标系。

载机的位置矢量与载机－目标的相对位置矢量之和为目标在导航坐标系中的位置矢量。当忽略载机位置的测量误差，载机雷达的测量误差就是目标位置的测量误差。

机载雷达系统的测量误差主要有:测距误差δD和测角误差(包括方位角误差 δψat和俯仰角误差δθat)。对式(6)进行微分得到:

将式(7)、式(8)代入式(5)，即可得到雷达测量误差造成的导引头指向误差为

2.3 初始对准误差对指向误差的影响

导弹在发射后，需要接收载机发送的目标信息。这就要求导弹必须建立一个与载机发送的信息所用坐标系一致的坐标系，这个坐标系通常采用载机惯性坐标系。空空导弹在发射前通过动基座对准可以建立一个导弹惯性坐标系，这个坐标系与载机惯性坐标系之间存在着一个对准误差。在惯导解算过程中，惯导初始对准误差将作为四元数初值代入到惯性导航计算方程，造成导弹的位置和姿态测量误差。

忽略其他误差因素，只考虑导弹初始对准误差的影响，导弹的姿态测量误差φb为

式中:φn0为载机惯性坐标系中的初始对准误差角。

将式(10)代入式(5)得到导弹姿态误差产生的导引头指向误差为

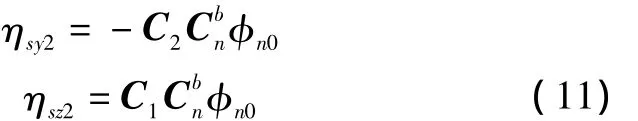
由于初始对准误差的存在造成计算的导航系n'与真实的导航系n不重合，有:

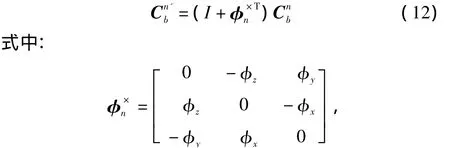
φx，φy，φz即为 φn在导航坐标系 3 个轴上的分量;，分别为本体系到计算导航系和真实导航系的坐标转换矩阵。

由于导弹的位置是在导航坐标系中对导弹速度进行积分得到，设初始速度没有误差，则导弹的位置测量误差只与加速度对时间的二重积分有关，即:

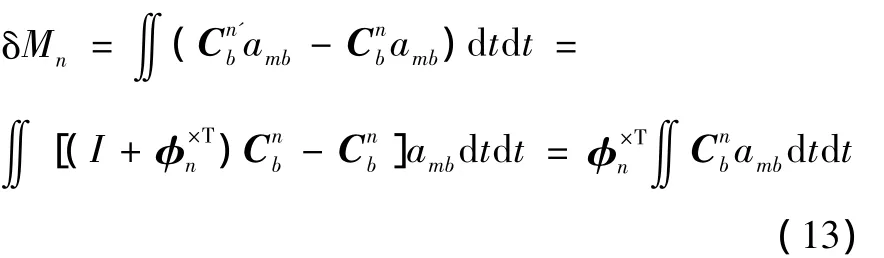
式中:amb为导弹加速度在本体坐标系中的投影。

设发射导弹后，载机开始作匀速直线运动，直到弹上导引头截获目标，可以近似认为导弹加速度在导航坐标系中的二重积分是导弹到载机的距离，即:

式中:Ramn为载机到导弹的距离向量。

将式(14)代入式(13)并进行坐标转换，得到初始对准误差造成的导弹位置误差为

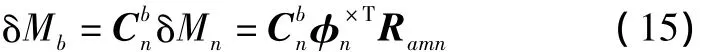
于是，由导弹位置误差产生的导引头指向误差为

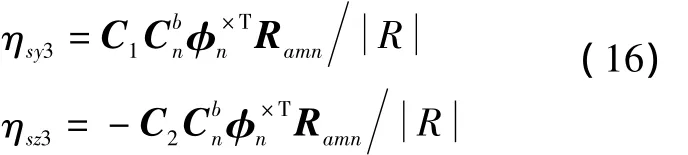
2.4 惯性元器件误差对指向误差的影响

捷联惯导系统的元器件误差主要包括加速度计测量误差和陀螺仪测量误差。

1)加速度计测量误差对指向误差的影响。

由于惯导系统是利用加速度计提供的比力数据计算导弹的位置。因此，加速度计的误差会造成导弹位置的测量误差。

加速度计的误差模型可表示为

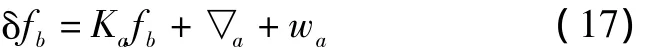
式中:Ka为加速度计一次项系数;fb为比力;▽a为加速度计常值偏置;wa为加速度计驱动白噪声。

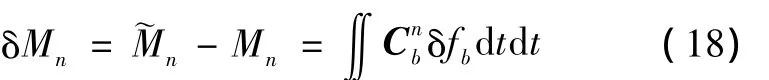
将式(17)代入式(18)得:

式中:fn为比力在导航坐标系中的投影，且fn=Cnbfb。

由于比力是载体惯性加速度与地心引力加速度之差，式(19)可以转化为

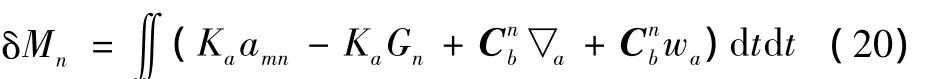
式中:amn表示导弹加速度在导航系中的投影;Gn表示地心引力加速度在导航坐标系中的投影。

由式(14)可知:

假定导弹飞行弹道为直线，导弹本体系与导航系的坐标转换矩阵保持不变，则有:

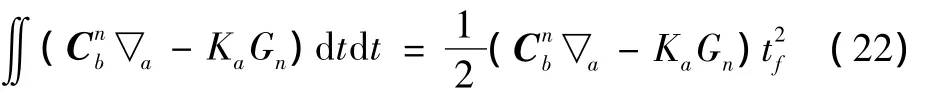
式中:tf表示中制导飞行时间。

将式(21)和式(22)代入式(20)，忽略白噪声误差，可得到:

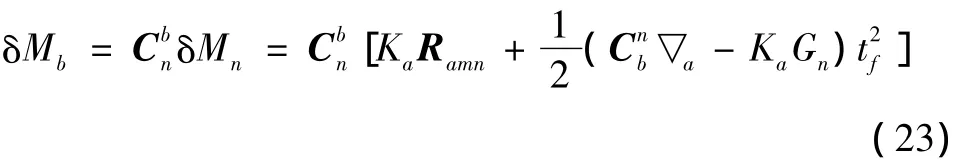
将式(23)代入式(5)得到加速度计测量误差造成的导引头俯仰和偏航方向指向误差为

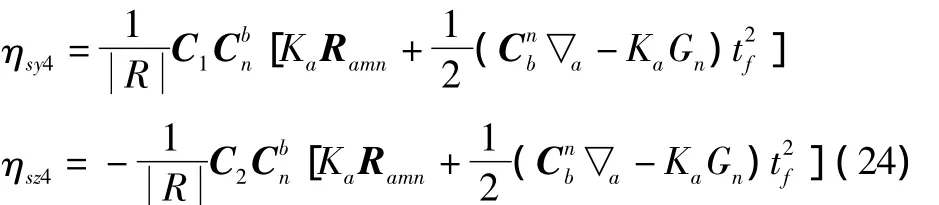
2)陀螺仪测量误差对指向误差的影响。

陀螺仪是导弹角运动的测量器件，对惯导系统的姿态误差产生直接影响。由陀螺仪造成的姿态测量误差会导致导航系统计算出的导航坐标系与真实的导航坐标系不重合。导弹位置的计算是在导航坐标系下进行的，因此陀螺仪的误差也会造成导弹位置的测量误差。

陀螺仪的误差模型可以表示为

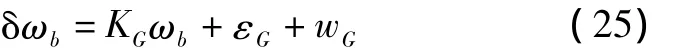
式中:KG为陀螺仪一次项系数;ωb为导弹的角速度;εG为陀螺仪的常值漂移;wG为陀螺仪驱动白噪声。

陀螺仪的误差造成导弹的姿态、位置测量误差。设陀螺仪量测的角速度为ω˜b，此时导弹的姿态误差φb为

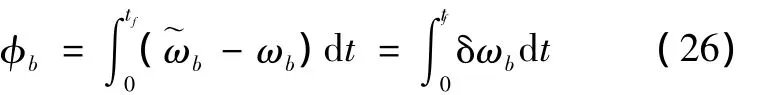
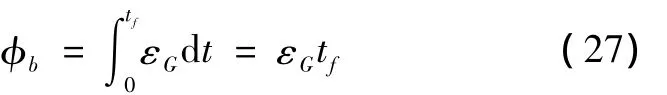
将式(27)代入式(5)得到陀螺仪测量误差导致的导弹姿态误差造成的指向误差为

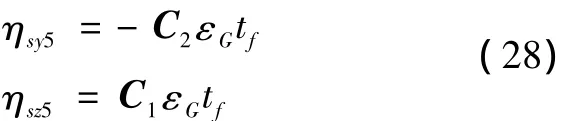
由陀螺仪误差造成的导弹位置测量误差为

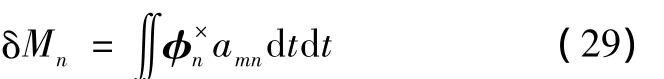
为简化计算，假设amn为常数，则陀螺仪的刻度因数误差为零。将式(27)代入式(29)得到:

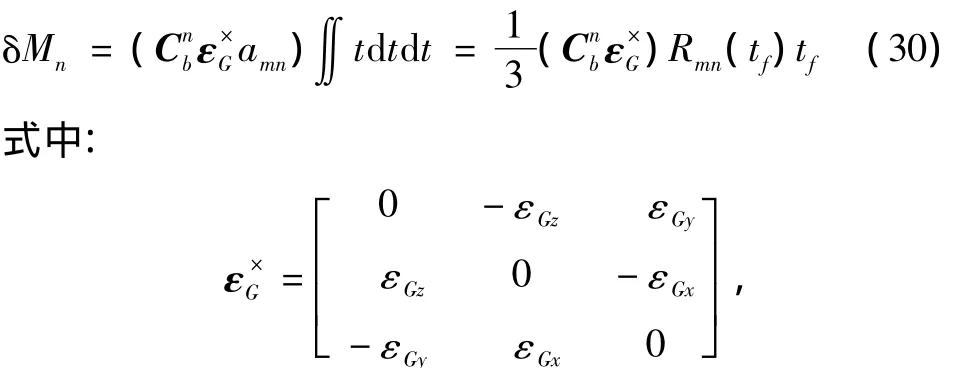
εGx，εGy，εGz为 εG在导弹本体坐标系中的 3 个分量;Rmn(t)表示导弹在导航坐标系中的飞行距离。

将式(30)代入式(5)，可得到由陀螺仪的测量误差引起的导弹位置误差造成的导引头指向误差为

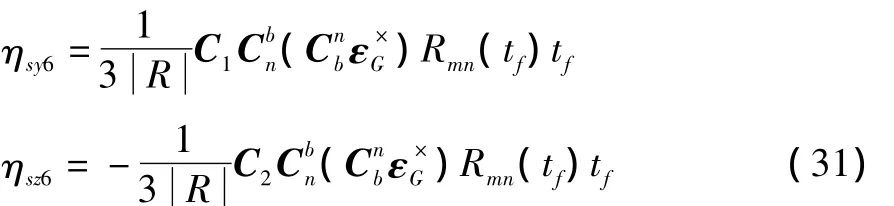
3 空空导弹采用纯惯导情况下的导引头指向误差

综合考虑初始对准误差、雷达测量误差、导弹惯性元器件误差3种误差源，为了直观地反映出3种误差源对指向误差大小的影响，采用方差分析法对指向误差进行研究。设 σsyj，σszj(j=1，…，6)是 ηsyj和 ηszj(j=1，…，6)的标准差。

根据文献［7］，由目标位置测量误差造成的导引头指向误差的标准差为

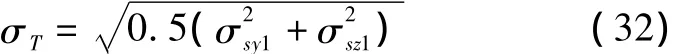
导弹姿态测量误差造成的导引头指向误差的标准差为

导弹位置测量误差造成的导引头指向误差的标准差为

利用合适的参数计算 σsyj，σszj(j=1，…，6)并将其代入式(32)～式(34)，得到 σT，σa和 σm随导弹攻击距离的变化，如图3所示。

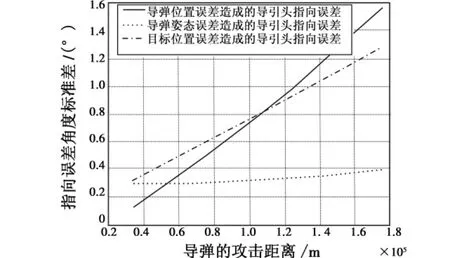
图3 3种误差因素对导引头指向误差的影响Fig.3 Effect of the three element errors on pointing-angle error of seeker

从图3可以看出:

1)导弹攻击的距离越远，导引头指向误差越大，其中σm随距离的增长最快，σT的增长在其次，σa增长最慢;

2)当导弹攻击较近距离(50 km以内)的目标时，σT最大，σa其次，σm最小;

3)当导弹攻击50～100 km的中距目标时，目标位置测量误差仍然是造成导引头的指向误差的主要因素，但σm已经超过σa，并且随距离的增长逐渐接近σT;

4)当导弹攻击100 km以上的远距离目标时，由导弹的位置测量误差造成的导引头指向误差最大，σT其次，σa最小。其中，当导弹的攻击距离达到180 km时，σm与σT相比超出20%，与σa相比超出75%。

可见，对于中远程空空导弹，导弹位置的误差是造成导引头指向误差的重要因素。为了减小指向误差，提高导引头角度截获概率，需要采用先进的导航系统能够为导弹连续提供高精度的位置信息。

4 捷联惯性/卫星组合导航系统对截获概率的影响

以惯性系统为基础的捷联惯性/卫星组合导航系统可以实现优势互补、取长补短。用卫星接收机提供的高精度定位信息通过组合滤波器来标定和补偿捷联惯导系统随时间积累的误差，提高导航精度。同时，利用捷联惯导系统的速度和加速度信息对卫星接收机进行速度辅助，以提高卫星接收机的抗干扰能力和动态性能［11］。

捷联惯性/卫星组合导航由于可以同时提供高精度的位置和速度信息，因此，在新一代中远程空空导弹上得到了广泛应用。根据表1所选中等精度的惯性元器件和GPS接收机误差参数，对捷联惯导系统与捷联惯性/卫星组合导航系统在中远程空空导弹中应用时导航系统性能进行了仿真比较，结果如图4所示。

图4 弹上导航系统的位置测量误差Fig.4 Locating error of navigation systems on missiles

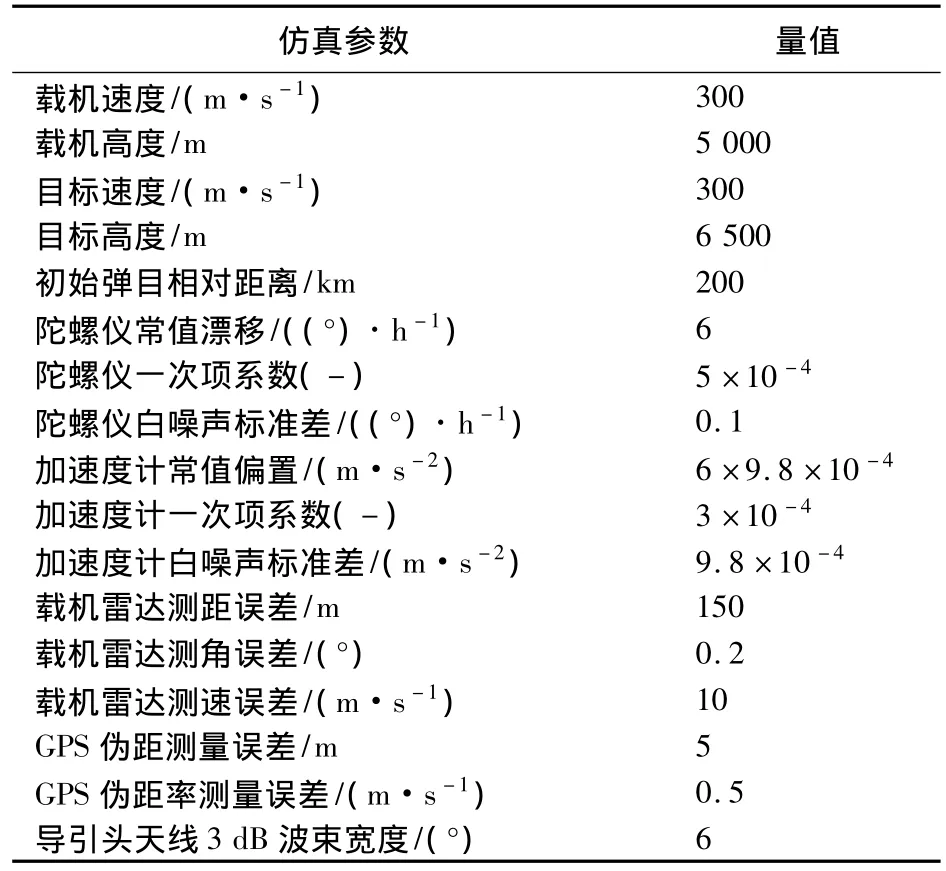
表1 蒙特卡罗仿真参数Table 1 Parameters of Monte Carlo simulation

从图4可以看出，捷联惯导系统的位置测量误差随时间积累。空空导弹飞行180 s，捷联惯导位置测量误差超过600 m。捷联惯性/卫星组合导航系统的位置测量误差小于15 m，而且不随时间积累。由于导弹的位置测量误差是造成导引头指向误差的主要因素，捷联惯性/卫星组合导航系统通过提高导弹的位置测量精度能够增加中远程空空导弹的截获概率。

下面采用蒙特卡罗方法，仿真验证空空导弹采用捷联惯性/卫星组合导航系统时，对导引头目标截获性能的影响情况。具体的仿真参数如表1所示。

图5中虚线代表导引头视场的范围，目标在视场范围内时表示可以被截获，否则无法被截获。利用蒙特卡罗仿真方法，根据300次仿真结果，将截获目标的次数与总的仿真次数之比作为目标的角度截获概率Pα。

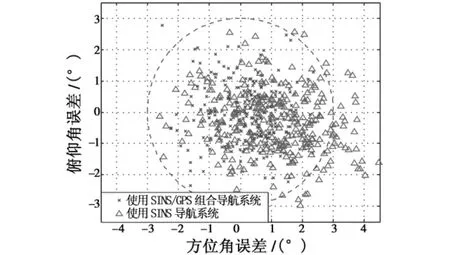
图5 目标在导引头视场中的分布Fig.5 Distributing of target in FOV of seeker

从图5可以看出，单独采用捷联惯性导航系统的情况下，目标在导引头视场中的分布范围大，在300次仿真过程中，只有250次落在导引头视场范围内，这种情况下目标角度截获概率的95%置信区间为(0.7870，0.8712);而当采用惯性/卫星组合导航系统时，目标落入导引头的视场299次，且集中分布在导引头视场中心周围，此时导引头的角度截获概率的95%置信区间为(0.9814，0.9994)。可见，与采用纯惯性导航系统相比，采用惯性/卫星组合导航系统时导引头的角度截获能力有很大提高。

导引头截获目标的概率P可以表示为

其中:Pr为距离截获概率。在弹载设备正常工作的情况下，通常认为Pr≈1。

结合速度截获概率和角度截获概率的计算结果，由式(35)可以得到采用捷联惯性/卫星组合导航系统，可使空空导弹在中、末制导交接时目标截获概率的95%置信区间由(0.7156，0.8110)提高到(0.8802，0.9431)。从而，惯性/卫星组合导航系统可以有效地减小导引头指向误差，并显著地提高了中、末制导交接时导引头对目标的截获概率。

5 结论

本文采用方差分析法对导引头指向误差进行了分析，利用蒙特卡罗仿真方法研究了惯性/卫星组合导航系统对空空导弹截获概率的影响。通过理论研究与具体分析，可得到以下结论:

1)随着导弹飞行距离的延长，导弹位置测量误差造成的导引头指向误差的增长速度超过雷达测量误差和初始对准误差造成的指向误差;

2)对于发射距离在100 km以上的远距空空导弹，导弹位置测量误差是造成导引头指向误差最重要的原因;

3)利用捷联惯性/卫星组合导航系统提高导弹中制导过程中的位置测量精度，可以有效地减小远程空空导弹中、末制导交接班时导引头的指向误差，提高对目标的截获概率。

［1］丁赤飙，毛士艺.主动寻的末制导的截获性能分析［J］.航空学报，1997，18(4):473-476.

［2］付海峰，刘华伟，张宗麟.中距主动制导空空导弹目标截获概率仿真计算［J］.电光与控制，2007，14(3):55-58.

［3］谢希权，易华.多目标攻击空空导弹的目标截获概率分析［J］.电光与控制，2001，8(2):33-36.

［4］查立宏，肖明清，谢希权.空空导弹发射后不管距离研究［J］.弹箭与制导学报，2003，23(2):11-13.

［5］廉建栋.中远程空空导弹的复合制导技术［J］.航空兵器，1990(1):1-5.

［6］朱莉，张国权，高向军.导引头交班精度的雷达误差分析［J］.火控雷达技术，2008，37(2):14-17.

［7］蓝伟华.火控系统误差与雷达型空空导弹截获目标概率计算［J］.电光与控制，2004，11(3):14-16.

［8］齐凯.弹脉冲雷达多目标检测技术的研究［D］.哈尔滨:哈尔滨工业大学，2006.

［9］KOUBA J T，BOSE S C.Terminal seeker pointing-angle error at target acquisition ［J］.IEEE transactions on aerospace and eletronic systems，1980，16(3):313-319.

［10］刘海军，王丽娜.复合制导防空导弹中末制导交班问题研究［J］.现代防御技术，2006，32(2):29-33.

［11］彭允祥.捷联惯导与导航卫星组合技术的发展趋势［J］.导弹与航天运载技术，1999(4):58-62.