大跨度双线无砟轨道预应力简支箱梁梁端锚固区应力分析

张玉文

(铁道第三勘察设计院集团有限公司,天津 300142)

1 概述

双线无砟轨道 56 m预应力混凝土简支箱梁是目前国内铁路客运专线建设中实施的最大跨度的双线无砟轨道简支梁跨,梁体自重超过2000 t,所以梁体配设了大量的预应力钢束。为了满足铺设无砟轨道的技术条件,对结构的刚度和铺设无砟轨道后的梁体变形均提出严格的要求。纵向钢束均在梁端进行张拉,由于梁跨较大,且大批的大吨位钢束集中在梁端进行锚固,使得梁端局部在锚下集中荷载和大吨位支座反力作用下受力十分复杂。有时会引起一些部位混凝土拉应力过大,超出混凝土抗拉强度而在这些部位产生裂缝,威胁梁的使用性能,所以梁端锚固区在大吨位群锚作用下的受力行为分析至关重要。

2 主梁构造

2.1 梁截面构造

56m箱梁为单箱单室断面,总长度 57.1m,梁高为 5.3m,顶板厚 0.35m,腹板厚 0.5m,梁端局部加厚至 1.1m;底板厚 0.3m,梁端局部加厚至 1m,箱梁在梁端支点处设置 2.0m厚的端隔板。

2.2 锚固区构造

钢绞线:采用 7φ5mm高强度、低松弛预应力钢绞线,标准强度为 fpk=1 860MPa,锚下张拉应力为1 380MPa,Ep=1.95×105MPa,公称直径为 15.2mm。

预应力管道:预制段采用外径 90mm的橡胶棒抽芯成孔,湿接缝管道采用内径 90mm的金属波纹管成孔。

锚具:选用 OVM15-15型号及其配套产品。

梁端锚固体系如图1所示,沿梁轴线对称布置。

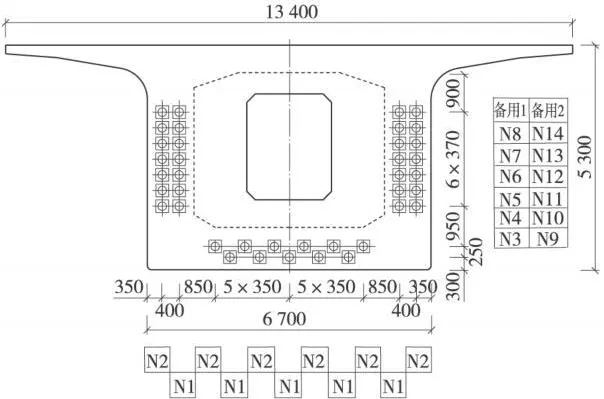
图1 56m箱梁端部锚固体系布置示意(单位:mm)

3 锚固区有限元模型

利用通用有限元分析程序 Ansys中为专门分析混凝土结构而开发的 Solid65单元对梁端结构进行了离散建模。为了提高计算效率,截取梁端一部分建立箱梁等比例实体模型,其中包括:封锚端,端部横隔板,箱梁端部变截面段,箱梁等截面段。

由于构件中的预应力钢束是空间曲线布置,因此考虑采用混凝土和钢束分离式建模,分别划分单元生成节点,然后通过节点耦合的方式模拟预应力钢束和混凝土之间的相互作用(该方法假定混凝土和钢束是有粘结的,并且不考虑混凝土中钢束的滑移)。为了使单元形状规则,加快求解速度和提高结果的正确性和精确度,在为模型划分网格时采用体扫掠的方法。

建模完成后对模型求解,在求解之前,为使钢束节点与混凝土节点在相应位置更好地耦合,钢束单元尺寸取为 0.5m,混凝土单元尺寸取为 0.11m,单元划分如图2所示。

图2 箱梁锚固区单元划分

4 箱梁锚固区应力计算

4.1 有限元计算结果

根据建立的有限元模型进行分析,主要计算结果如图3～图10所示。

箱梁采用 C50混凝土,轴心抗压强度为 33.5 MPa,轴心抗拉强度为 3.10MPa。由图3中的应力分布,根据圣维南原理,可以看出箱梁锚固区外侧混凝土处于受拉状态,拉应力均小于 0.5MPa,进入钢束布置区后,腹板和底板中的钢束附近混凝土处于受压状态,腹板中的压应力均小于 10.0MPa,底板中的压应力小于 11.0MPa,没有出现混凝土破坏。

由图4中应力分布可知,横隔板内主要承受压应力,压应力在 1.0MPa左右。

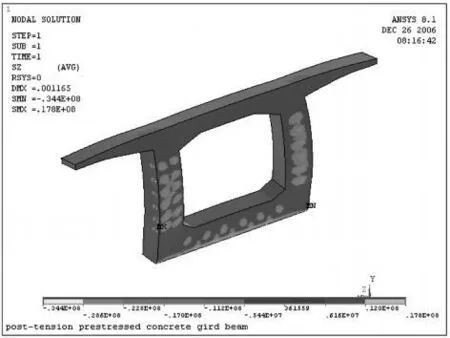
图3 支座梁端侧箱梁纵向正应力

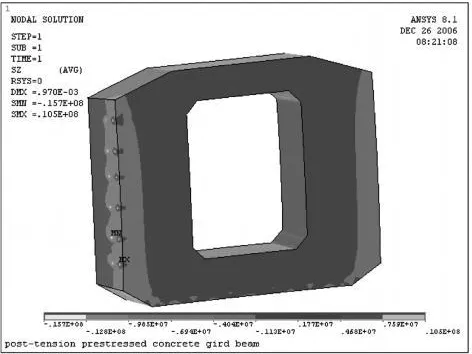
图4 支座梁端侧横隔板纵向正应力

由图5可知,箱梁腹板中的压应力在 7MPa左右,支座附近箱梁底板会产生拉应力,拉应力在 1 MPa左右。

由图6可知,由于横隔板在受力作用下变形而在内侧产生拉应力,向外逐渐发展为压应力,即在支座跨中侧横隔板内侧受拉外侧受压,拉应力小于 1MPa,压应力小于 6.5MPa。

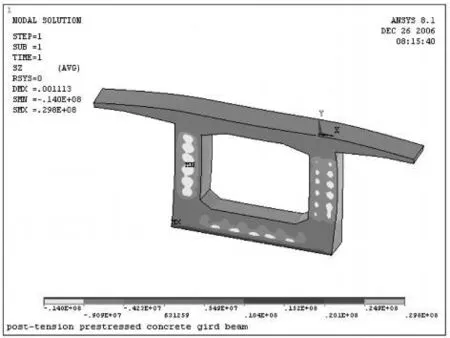
图5 支座跨中侧箱梁纵向正应力

由图7可知箱梁变截面段在预应力和重力作用下处于全截面受压状态,压应力均小于 20MPa。

由图8可知在等截面内箱梁全截面受压,压应力为 16MPa左右。

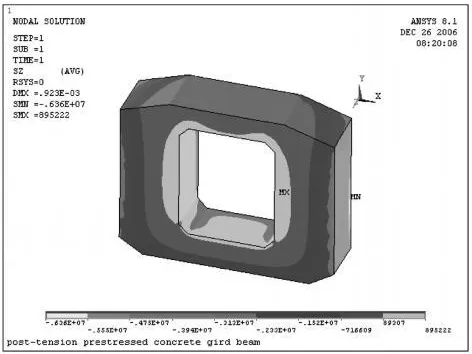
图6 支座跨中侧横隔板纵向正应力

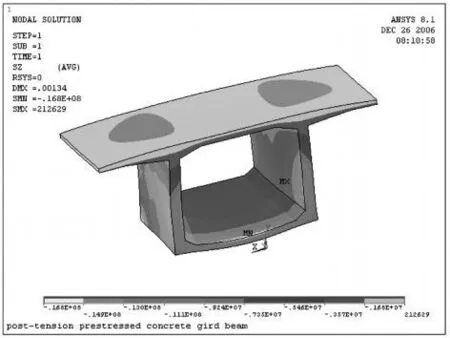
图7 箱梁变截面段纵向正应力

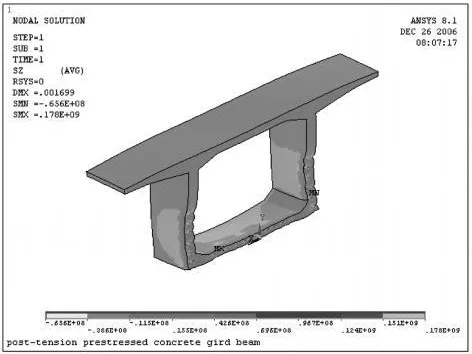
图8 箱梁等截面段纵向正应力

由图9可知在箱梁的腹板、底板以及腹板与底板相交处的加腋处都会产生拉应力,拉应力大小维持在1MPa左右。顶板底面中心附近拉应力比较大,最大达到 1.8MPa左右。

由图10可知,横隔板中分布的横向正应力主要为拉应力,箱梁端头侧横向拉应力大于靠近支座侧拉应力,最大拉应力达到 1.8MPa。值得注意的是,在腹板内侧倒角附近有应力集中现象发生,其最大拉应力可达 2.5MPa左右,容易使混凝土拉坏。

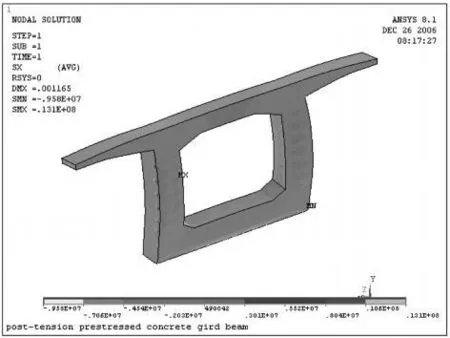
图9 支座梁端侧箱梁段横向正应力

4.2 应力计算结果分析

通过以上计算分析,证实箱梁在预应力和自重荷载作用下在梁端张拉钢束附近,会出现混凝土拉应力偏大现象,尤其是在箱梁横隔板腹板和底板交汇处的横向拉应力集中情况比较突出。另外,在箱梁变截面段的腹板内侧和箱内两侧下倒角处也容易出现拉应力。在预应力荷载和自重荷载作用下梁端横隔板承受较大的压应力。

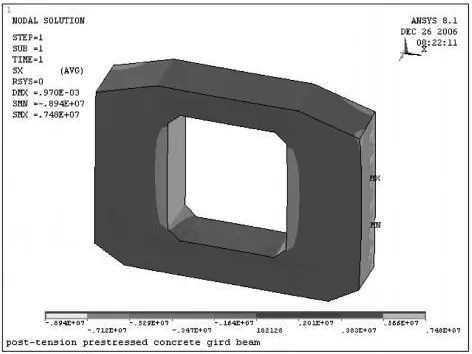
图10 支座梁端侧箱梁横隔板横向正应力

5 箱梁锚固区应力试验研究

为验证该 56m箱梁梁端在群锚作用下的承压强度和抗裂性,在实际张拉施工时进行了梁端锚固区试验研究,并对前述有限元仿真结果进行对比验证。

5.1 应变传感器测点布置

端部梁块混凝土浇筑前,在锚固区域预埋应变传感器。传感器的布置位置和方向见图11,纵向表示沿z轴方向放置,横向表示沿 x轴放置即腹板板厚方向,竖向表示沿 y轴方向放置。

锚下的应力情况比较复杂,尤其在距端部 1m范围内,应力的变化比较大,测点的布置主要是测锚下三向应力的变化情况。 1号、3号、5号、7号、10号、12号、14号、15号测锚下纵向应力,2号、4号、6号 、8号测锚下横向应力,9号、11号、13号测锚下竖向应力。

5.2 预应力束张拉程序

张拉程序:0→初应力(0.1σcon)→控制应力 σcon→持荷 5min→锚固。张拉按左右对称原则进行,最大不平衡束不超过一束,张拉按以下顺序进行:2N3-2N9-2N4-2N10-2N5-2N11-2N6-2N12-2N7-2N13-2N8-2N14-6N2-5N1,平均每张拉 4束预应力钢束对应变传感器进行一次测试。

5.3 实测结果与理论结果比较分析

下面将各个测点在各张拉工况下的应力变化列于表1。

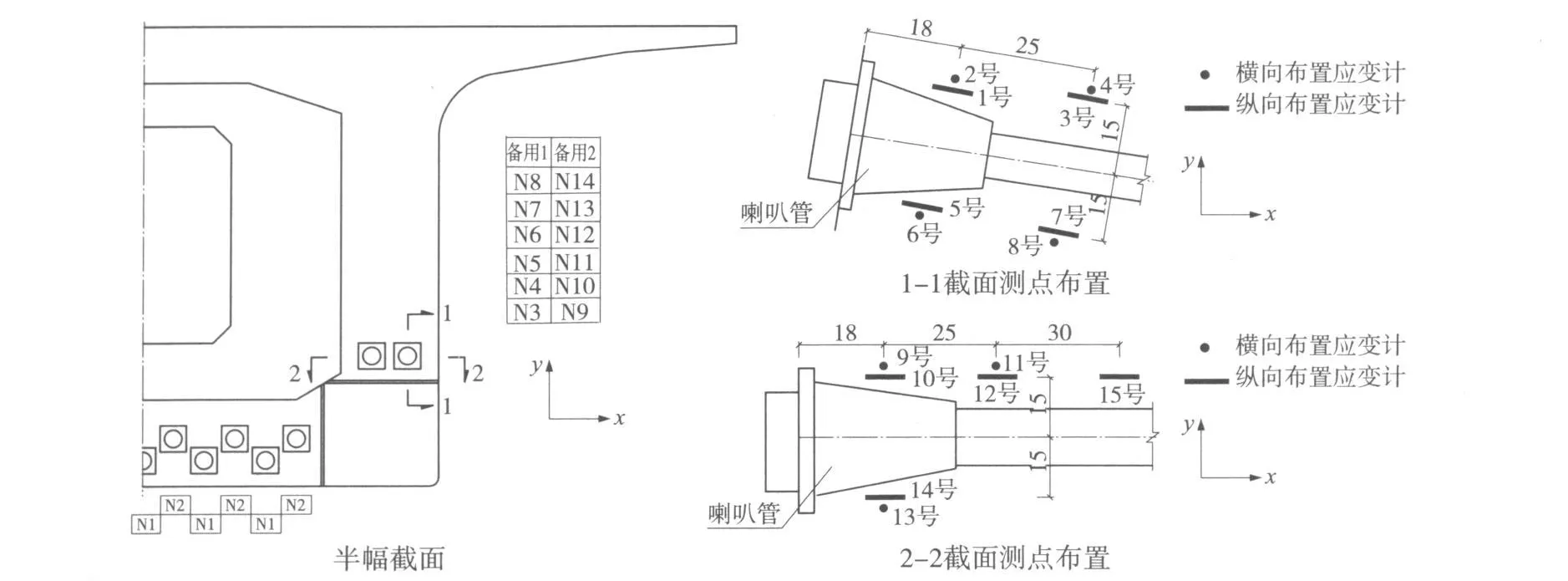
图11 传感器测点布置(单位:cm)

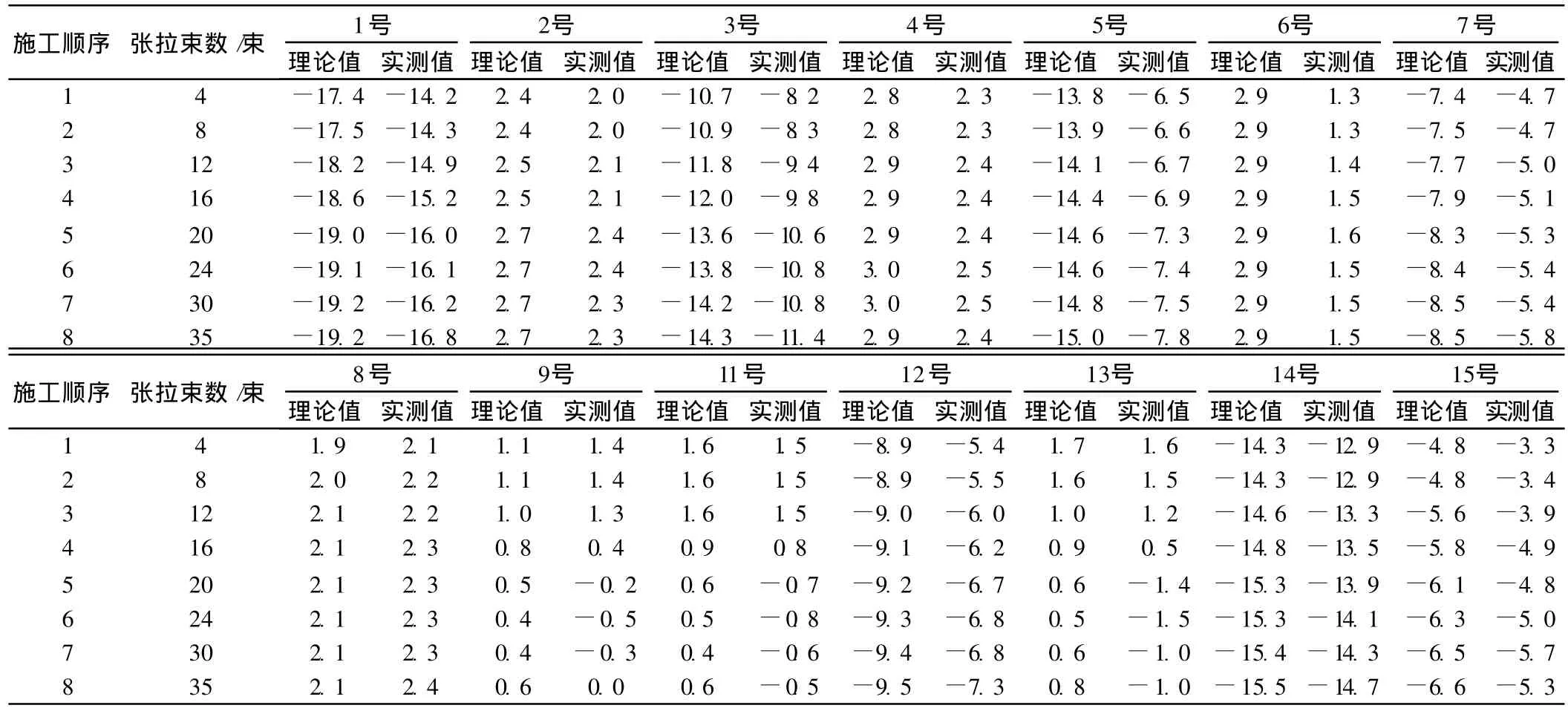
表1 测点理论应力与实测应力对比MPa

由实测结果主要得出以下结论:

测点位于 N9锚下,从测点在各张拉工况下应力变化规律可以看出,实测值和理论计算值的变化趋势一致,张拉测点所在预应力束时锚下的纵向压应力骤然变大,随后张拉工况下,应力有所增大,但对测点应力的变化影响不大。测点处锚下纵向应力主要是测点所在的预应力束张拉作用的结果,其他工况张拉时,测点的纵向应力有所增大是因为测点在箱梁的中性轴偏下方,受压增大。

6 结语

综合分析计算结果及试验数据,按有限元分析群锚效应,其应力均未超出容许值。在各张拉工况下,张拉测点以外的预应力束对锚下纵向应力和横向应力的影响不大,对竖向应力的变化有一定影响。实测值和理论值变化规律相似,说明锚下应力的分布主要是由测点处的预应力作用所引起的。现场试验结果与理论分析结果较为吻合,验证了理论分析的建模、边界条件模拟以及加载形式的正确性。为大吨位群锚作用下合理梁端构造形式的选择以及梁端局部受力分析提供可借鉴的工程实践经验。

[1]江见鲸,陆新征,叶列平.混凝土结构有限元分析[M].北京:清华大学出版社,2005.

[2]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007.

[3]清华大学建工系.大吨位预应力锚固区混凝土局部承压问题研究[C]∥中国建筑科学研究院钢筋混凝土结构研究报告选集.北京:中国建筑工业出版社,1981:255-288.

[4]张吉柱.密布预应力束锚具下混凝土局部受压承载力计算方法的研究[S].哈尔滨:哈尔滨工业大学,2003.

[5]TB10002.3—2005,铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S].

[6]王增荣,李之榕.预应力混凝土梁锚下局部应力的研究[J].铁道学报,1982,4(4):49-54.

[7]陈忠炎.预应力混凝土箱梁桥局部锚固应力[J].国外公路,1994,14(6):43-46.