VPRS在轴承故障诊断中的应用

沈仁发，祁彦洁，康海英，郑海起，陈孝平，张俊武

(1.军械工程学院 火炮工程系，石家庄 050003;2.徐州空军学院 基础部，江苏 徐州 221000；3.77611部队 55分队，拉萨 850000；4.65571部队，吉林 四平 136000)

对齿轮箱进行故障诊断时，常常以单级齿轮箱为研究对象[1-4]，然而在实际生产中，许多机械设备的齿轮箱为二级甚至多级机构，传动结构更加复杂。另外，在故障诊断振动分析中，往往将试验条件假设为机械设备处于恒定工况，即转速和载荷都稳定的状态，有的甚至是在空载状态下工作，但对变载荷、非稳态工况下的研究很少。事实上，许多旋转机械常常是在变载荷、非稳态情况下运行的。旋转机械在载荷变化时，其转速、振动信号、噪声信号等都会随着载荷的变化而改变，测得的信号是典型的非稳态信号，此时基于传统稳态过程的诊断方法已不再适用，只有使用基于非稳态过程的方法对其进行诊断。同时，由于机械振动的非稳态信号中往往包含的信息量比稳态振动信号更为丰富，能够反映出更多的系统特性，在稳态情况下不容易显现出来的信息在变载荷条件下可以得到充分的体现，对齿轮箱变载荷情况下的研究显得更为重要。因此，尝试以二级减速的齿轮箱为研究对象，对其变载荷过程进行分析，以解决复杂结构、变载荷条件下齿轮箱故障诊断精度问题。

基于知识的诊断方法应该是一种很有前途的方法，尤其是在上述复杂结构、变载荷条件下齿轮箱的故障诊断领域。下面拟用变精度粗糙集理论挖掘不确定数据间的关系，发现潜在知识，力求将由存在大量冗余信息和矛盾信息小规模的对象集中得到的结论，应用到大规模的对象中去[5]。

1 变精度粗糙集理论

粗糙集(Rough Sets,RS)理论[6]以其简单实用的特点，已在故障诊断、模式识别、数据挖掘、图象处理等领域得到了广泛应用。但是，粗糙集理论缺乏对复杂系统的处理机制，对于不确定性概念的边界区域刻画过于简单，缺乏对噪声数据的适应能力。在数据集存在噪声等干扰以及数据小样本情况下，基本RS模型会由于对数据的过拟合而使其对新数据的预测或分类能力大为降低[7]。为增强RS模型的抗干扰能力，Ziarko W提出了一种变精度粗糙集模型(Variable Precision Rough Sets，VPRS)，通过引入一个误差精度，即分类错误率β(0≤β<0.5)，使其具有一定的容错性[5]，即允许存在一定程度的错误分类率，当β=0时，VPRS模型就是基本RS模型了。Aijun An提出了一种变精度粗糙集模型[8]，引入β(0.5≤β<1)作为正确的分类率。

1.1 基本概念

定义1：设X和Y表示有限论域U的非空子集，如对于任意x∈X，有x∈Y，则称Y包含X，记作Y⊇X。X关于Y的相对错误分类率c(X,Y)定义为：

式中：|X|为集合X的基数。

定义3[9]：设S=(U,A=C∪D,V,f)为一决策信息系统，B⊆C，论域U上由B和D所产生的等价关系分别为RB和RD，它们在U上产生的划分分别为：

U/RB={[x]B|x∈U}={X1,X2,…,Xn}，

U/RD={[x]D|x∈U}={D1,D2,…,Dn}。

其中,[x]B={y∈U|∀b∈B,f(x,b)=f(y,b)}，[x]D={y∈U|∀d∈D,f(x,d)=f(y,d)}，分别是x关于B和D等价类。

定义4[9]：对任意Z⊆U,B⊆C,β∈(0.5,1]，定义Z关于B的β正域、负域以及边界域分别为：

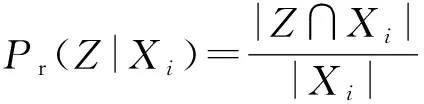
定义5[9]：设B⊆C，定义近似分类质量为：

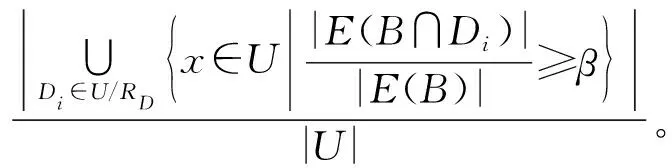
其中,γβ(B，D)仅依赖于β的取值，近似分类质量表示的是在论域中给定某一β值时，应用现有知识可能正确地划入决策类的百分比。

定义6[9]：设决策信息系统S=(U，A=C∪D，V，f)中，U/RD={D1,D2,…,Dn},β∈(0.5,1]，条件属性C关于决策属性D的一个β约简为REDβ(C,D)，其必须满足以下两个条件：

(1)γβ(C,D)=γβ(REDβ(C,D),D)；

(2)从REDβ(C,D)中去掉任何一个属性，都将使(1)不成立。

1.2 变精度粗糙集应用步骤

变精度粗糙集理论模型能够借助约简有效地消除大量的冗余信息，从而得出正确的诊断规则。

1.2.1 决策表

知识系统可以方便地用数据库中的表格表达，列表示属性，行表示记录。每行表示该记录的信息，表中的每个值都是对应行(记录)在对应列(属性)下的值，即为属性值。

1.2.2 连续属性离散化

由于粗糙集理论只能处理离散属性，欲从一个具有连续量的决策表中提取知识，首先要对条件属性的值域进行离散化处理。在粗糙集理论中，常用的离散化方法有等间距法、等频距法、最小熵法等。

1.2.3 条件属性约简

决策表的简化就是化简决策表中的条件属性，化简后的决策表具有化简前的决策表的功能，但化简后的决策表具有更少的条件属性，即同样的决策可以基于更少的条件。按照定义6，本文的条件属性约简采用如下步骤：

(1)初始化：对离散化后的属性决策表，令RED=C；

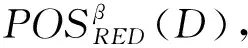
(3)对每一个属性ci按定义5求出近似分类质量γβ(RED-{ci},D)；

(4)逐个比较γβ(RED-{ci},D)和γβ(RED,D)是否相等，若全不相等，则RED即为最简条件属性子集；否则，按广度优先搜索策略，约去第一个使两式不相等的属性ci，即RED=RED-{ci}，转步骤(2)；

(5)得到一个β变精度属性约简，从而得到简化的决策规则。

1.2.4 决策规则提取

在提取规则时，要对决策规则进行约简[10]：(1)删除条件简化后的决策表中相同的诊断规则；(2)在不改变决策表相容性的前提下，删除每一条故障分类规则中多余的属性，只保留必要的属性。

2 轴承故障诊断实例

2.1 信号的采集与处理

在某型二级齿轮箱上进行试验验证，齿轮箱测试的结构简图如图1所示。

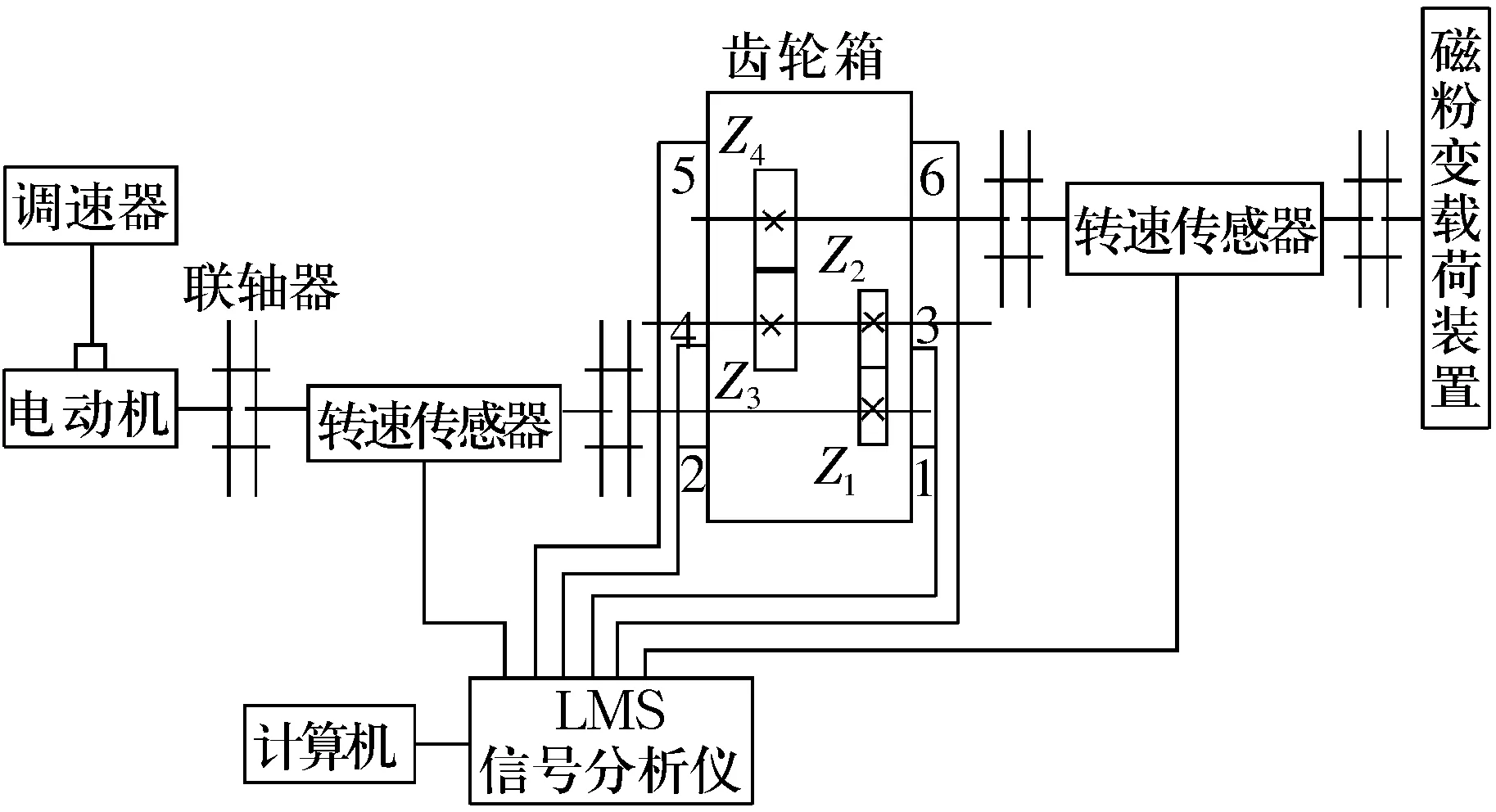
图1 齿轮箱测试的结构简图

在测试系统中，激励通过电动机、输入轴、中间轴、输出轴传递。总传动比为9，输入轴的主动齿轮齿数Z1=25，中间轴的被动齿轮齿数Z2=50，主动齿轮齿数Z3=18，输出轴的被动齿轮齿数Z4=81。输入轴端轴承型号为6305，中间轴端轴承型号为6206，输出轴端轴承型号为6209。在输入轴、中间轴、输出轴的轴承内圈和外圈分别加工长为内、外圈各自高度，宽为0.5 mm，深为1.5 mm的小槽用来模拟轴承内圈和外圈裂纹，一共6种故障工况。对齿轮箱的变载荷过程进行分析，由空载加至80 N·m左右共耗时21 s，将由B&K4508振动加速度传感器测得的振动信号传给LMS信号分析仪进行数据处理，采样频率为16 384 Hz。对正常工况和上述6种故障工况分别测取30组数据，其中20组用作训练数据，10组用作待诊数据。

图2为某组中间轴轴承正常和外圈故障信号，由图可以看出：信号的幅值随载荷的升高而逐渐增大，但不能判断故障的类型。图3为某组中间轴轴承外圈故障信号用小波包消噪后的时间历程，由图可看出有一定的效果，即消噪后信号中的冲击成分比较明显。

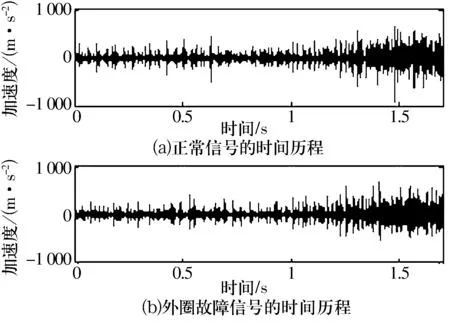
图2 轴承正常和故障信号

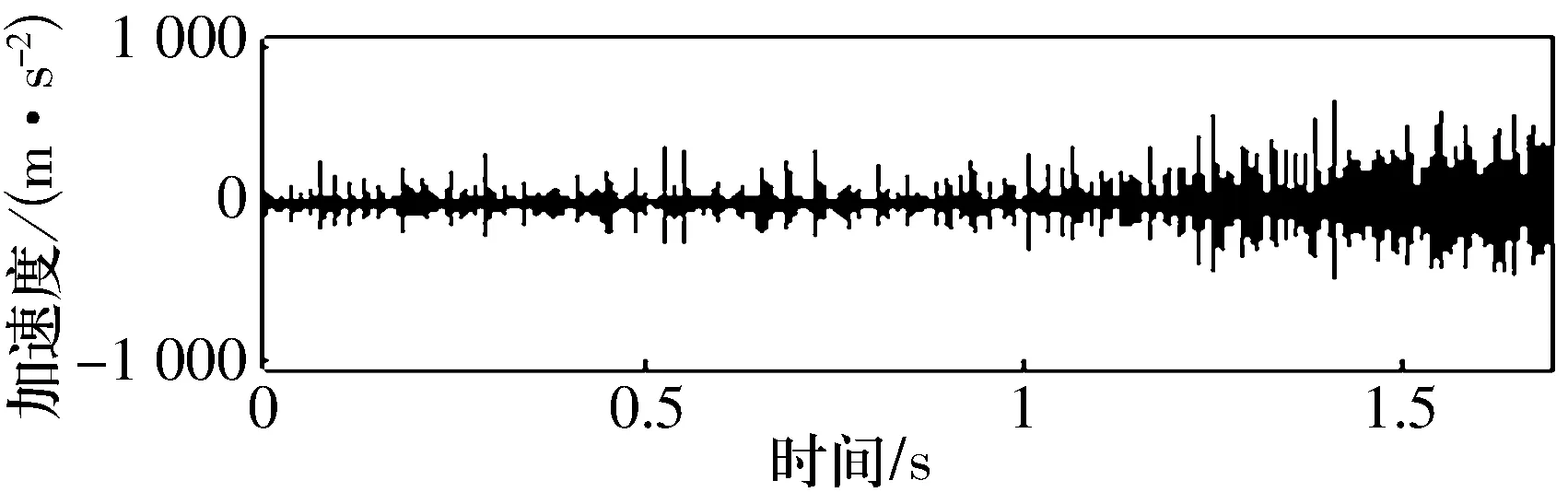
图3 小波包消噪后外圈故障信号

以滚动轴承的运行状态为研究对象，针对轴承的7种工况，分别从20组待训练样本中任取3组，形成论域U={x1,x2,x3,…,x21}。对消噪后的各组信号用db1小波进行二层小波包分解，分解后，各频段信号的能量特征值综合了信号在时域和频域内所包含的全部故障信息。对各频段内的信号能量进行统计分析，形成反映故障信号的特征向量，得到4个归一化的特征向量T′=[E20/E，E21/E，…，E23/E]。

以这4个特征参量为条件属性C，分别用a,b,c,d表示，即C={a,b,c,d}。以滚动轴承的运行状态为决策属性，用D表示，其中1为正常状态，2为输入轴端轴承内圈故障状态，3为输入轴端轴承外圈故障状态，4为中间轴端轴承内圈故障状态，5为中间轴端轴承外圈故障状态，6为输出轴端轴承内圈故障状态，7为输出轴端轴承外圈故障状态。利用所提取的特征参量，建立如表1所示的滚动轴承的训练样本数据。

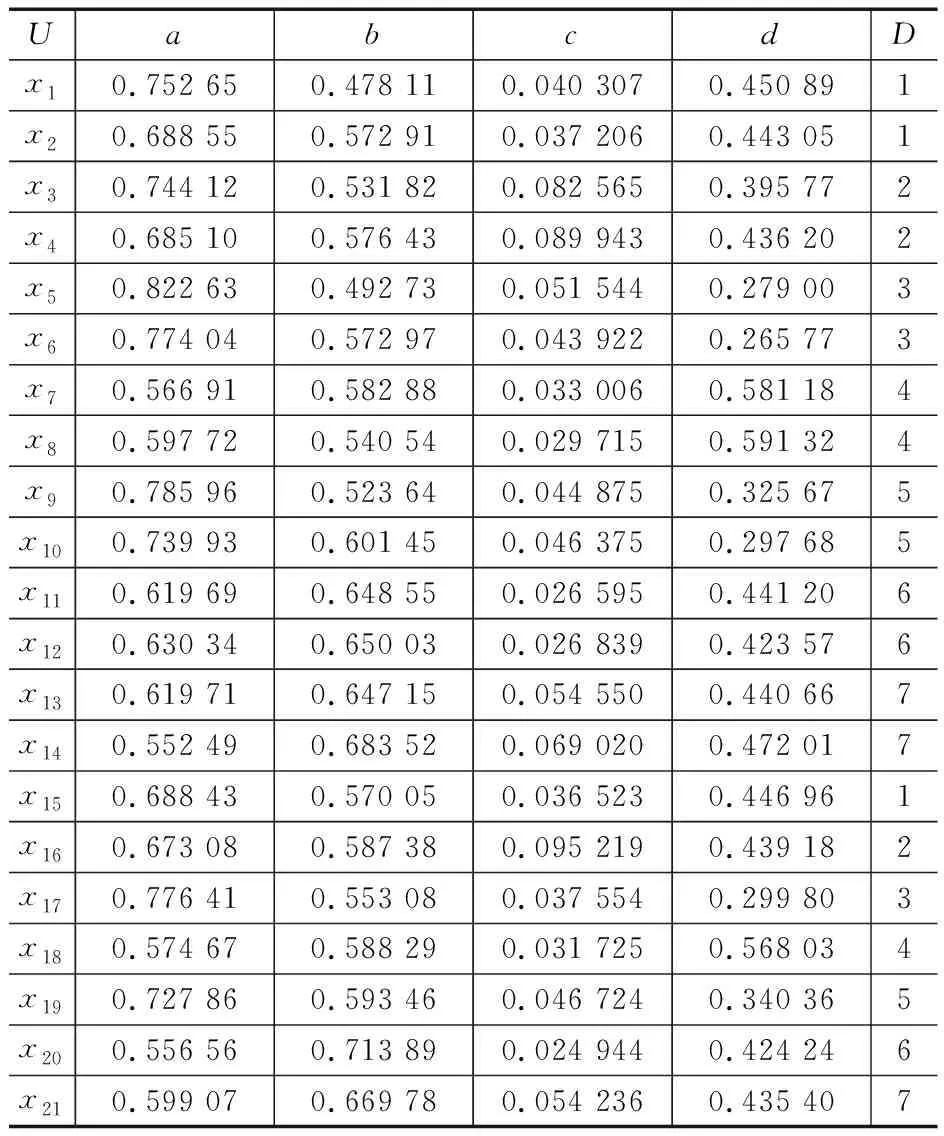
表1 训练样本数据

变精度粗糙集也只能处理离散属性值，而原始故障属性值是连续的，因此必须对数据进行离散化处理。采用等间距法得到如表2所示的数据离散化结果。

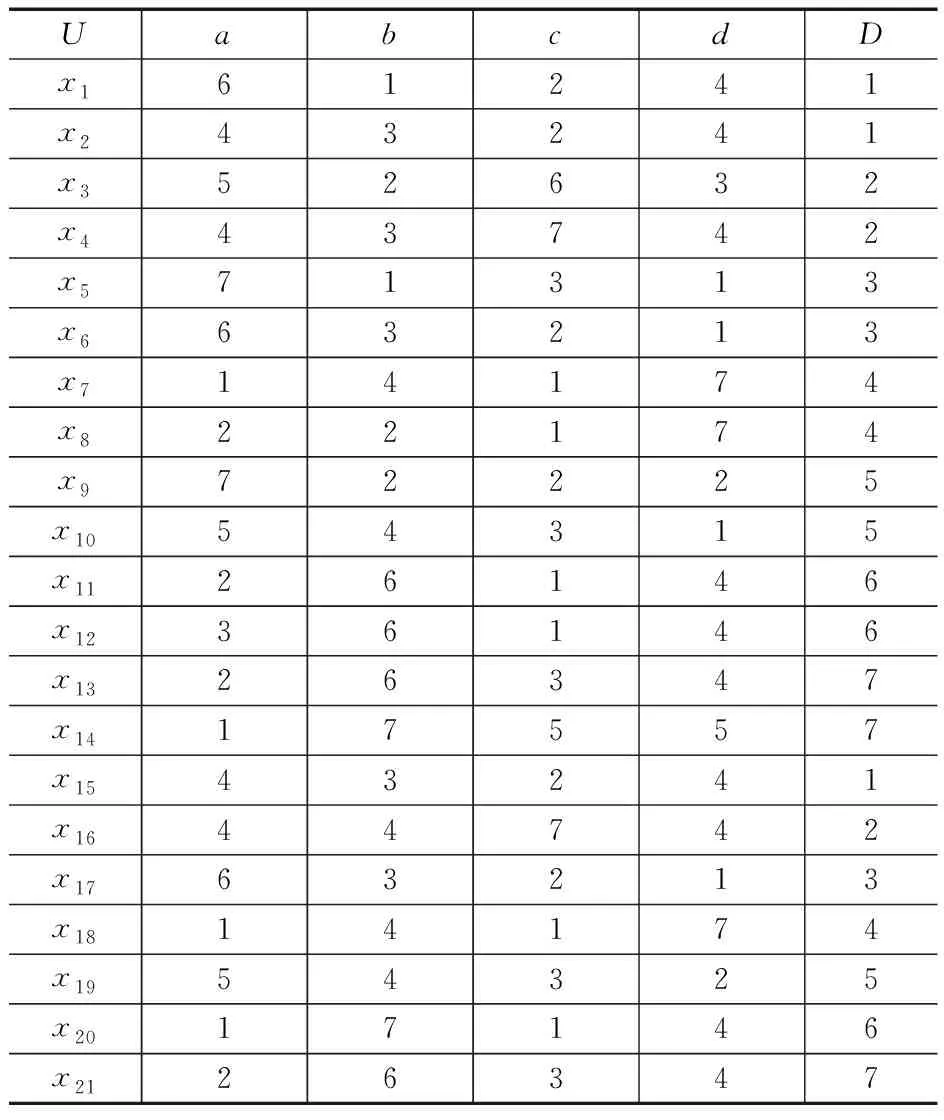
表2 数据离散化结果

2.2 β的约简

由于随着β的增加，变精度粗糙集意义下的不确定区域变小，提取规则的确定性增强，但容错性降低，当β=1时，变精度粗糙集变为标准粗糙集。因此，β粗糙集对数据不一致性有一定的容忍度，在某些场合可以更好地抗噪声，增强产生规则的鲁棒性，下面对表2的条件属性集合进行β近似约简。

计算决策表的条件类分别为：X1={x1}，X2={x2,x15}，X3={x3}，X4={x4}，X5={x5}，X6={x6,x17}，X7={x7,x18}，X8={x8}，X9={x9}，X10={x10}，X11={x11}，X12={x12}，X13={x13,x21}，X14={x14}，X15={x16}，X16={x19}，X17={x20}。

同理，决策类分别为：D1={x1,x2,x15}，D2={x3,x4,x16}，D3={x5,x6,x17}，D4={x7,x8,x18}，D5={x9,x10,x19}，D6={x11,x12,x20}，D7={x13,x14,x21}。

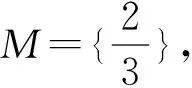
2.2.1β=0.65时的约简

按照定义4可计算得到：

γ0.65(RED,D)=1，

γ0.65(RED-{a},D)=1，γ0.65(RED-{b},D)=1，

γ0.65(RED-{c},D)=1，γ0.65(RED-{d},D)=1。

显然约去每个属性后近似分类质量都不变。按照广度优先搜索策略，先约去属性a，得RED=C-{a}。

显然β近似约简为RED={b,c,d}，此时在上述约简的基础上，得到10条β近似决策规则：

Rule1：IF“c=2”and“d=4”THEN1正常；

Rule2：IF“b=2”and“c=6”and“d=3”THEN2输入轴端轴承内圈故障；

Rule3：IF“c=7”and“d=4”THEN2输入轴端轴承内圈故障；

Rule4：IF“b=3”and“c=2”and“d=1”THEN3输入轴端轴承外圈故障；

Rule5：IF“b=1”and“c=3”and“d=1”THEN3输入轴端轴承外圈故障；

Rule6：IF“c=1”and“d=7”THEN4中间轴端轴承内圈故障；

Rule7：IF“b=4”and“c=3”THEN5中间轴端轴承外圈故障；

Rule8：IF“b=2”and“c=2”and“d=2”THEN5中间轴端轴承外圈故障；

Rule9：IF“c=1”and“d=4”THEN6输出轴端轴承内圈故障状态；

Rule9：IF“b=6”and“c=3”and“d=4”THEN7输出轴端轴承外圈故障；

Rule10：IF“b=7”and“c=5”and“d=5”THEN7输出轴端轴承外圈故障。

2.2.2β=0.75时的约简

按照定义4可计算得到：

γ0.75(RED,D)=1，

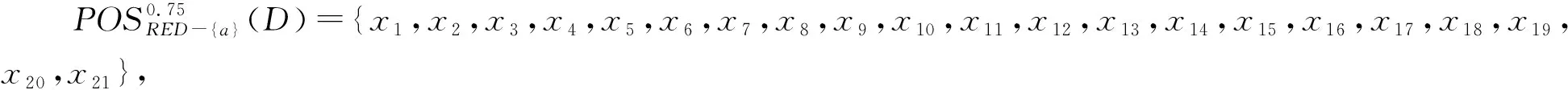
γ0.75(RED-{a},D)=1，γ0.75(RED-{b},D)=1，

显然c为核属性，继续计算得：

因此，{c}不是β近似约简。

显然{c,d},{c,b},{c,a}都不是β近似约简。

因此，有3种β近似约简RED={c,a,b},{c,a,d}或{c,b,d}。

通过上述的β近似约简可以得到不同的β近似决策规则，最后可利用β近似决策规则对滚动轴承故障情况进行诊断。

3 结束语

以二级减速的齿轮箱为研究对象，对其变载荷过程进行了分析，探讨了变精度粗糙集在轴承故障诊断中的应用，提出了一种故障决策规则提取方法。通过引入集合M，把β分成不同的区间，对不同的β取值讨论β近似约简，得到β近似决策规则 。目的在于解决传统故障诊断中从噪声故障信息中自动获取诊断规则这一难题，增强了数据分析和处理的鲁棒性，该方法还可以应用于其他旋转机械的故障诊断中。