径向滑动轴承弹流润滑耦合求解

张 勇，莫森泉，王 佳

(华南理工大学 机械与汽车工程学院，广州 510640)

径向滑动轴承的润滑问题通常是根据流体动压理论，采用Reynolds方程求解。随着工程应用的要求，目前滑动轴承的轴承衬倾向于采用低弹性模量材料，在重载高速工况下，摩擦副表面的最大弹性变形量可以达到甚至超过最小油膜厚度，润滑油黏度也会因重载而增加。因此，在进行重载径向滑动轴承润滑特性分析和计算时，必须考虑摩擦副表面的弹性变形及润滑油黏度的增加对润滑的影响。

径向滑动轴承弹性流体润滑问题求解的难点是需要联立求解Reynolds方程和弹性变形方程。

弹性变形数值计算耗时长，其算法又会影响求解稳定性和收敛程度。求解弹性变形时，或采用Winkler假定的弹性位移方程对动载滑动轴承的弹流润滑状况进行分析[1]；或采用Boussinesq解的弹性位移方程对径向轴承的弹性流体润滑问题以及重载径向滑动轴承的润滑力学问题和数值求解方法进行分析和研究[2-4]。但是上述两种弹性位移方程在力学模型的建立上都存在一定缺陷，Winkler弹性位移方程假设模型是一维的，而Boussinesq解的弹性位移方程假设模型是半无限体，两者都与实际情况相差较大。此外，文献[5-6]采用柔度矩阵法来研究径向滑动轴承的弹流润滑问题及数值计算方法，但是柔度矩阵法以弹性位移与压力成线性关系为前提，只是弹性变形的一种简化求解方法。文献[7]使用Matlab与ANSYS软件共同构建了弹流润滑软件求解环境，对弹流润滑数值耦合求解进行了尝试，但两种软件间数据传输时需要人工控制，如果迭代次数较多，计算会变得非常繁琐。文献[8]提出了一种耦合算法来研究滑动轴承弹性变形问题，在每一次压力的迭代过程中同时计入弹性变形对压力分布的影响，采用有限元法求解弹性变形，对轴承弹流润滑问题的求解进行了有益尝试。

由于数值求解过程中，滑动轴承的油膜压力与弹性变形是不断变化并相互影响的，同时，两者之间不是简单的线性关系，必须整体考虑油膜压力对弹性变形的影响，并将弹性变形返回Reynolds方程的求解过程中，因此，需建立一种液固耦合算法。本文基于这种思想采用ANSYS软件提出了一种新的耦合算法，可以有效地进行径向滑动轴承的弹流润滑问题的研究。

1 润滑方程

1.1 润滑基本方程

对于有限长径向滑动轴承，润滑介质在轴承间隙空间中的流动服从Reynolds方程，在轴承处于稳定运转或静态工况下，不考虑温度变化时，可采用如下简化的二维Reynolds方程[9]：

(1)

式中：p为油膜压力分布函数，p=p(x，z)；x为轴承圆周方向；z为轴承轴向；h为油膜厚度函数，h=h(x)；U为轴颈线速度；μ为润滑油动力黏度。

对轴承进行润滑性能分析时，常以无量纲形式进行，(1)式的无量纲形式为[10]：

(2)

式中：H为无量纲油膜厚度，H=h/c，c为轴承半径间隙；P为无量纲油膜压力；d为轴颈直径；L为轴承宽度；φ=x/r，r为轴承半径，0≤φ≤2π；λ=2z′/L，z′为轴承轴向坐标；如果坐标原点取在轴承轴向中央，则-1≤λ≤1。

1.2 黏压方程

这里采用指数关系的黏压方程：

μ=μ0eαp

(3)

式中：μ0为环境压力下润滑油的动力黏度；α为黏压指数。

1.3 润滑油膜方程

考虑弹性变形时，润滑油膜的膜厚方程为：

h(x,y)=h0(x,y)+δ(x,y)

(4)

式中：h0(x，y)为刚性膜厚项；δ(x，y)为弹性膜厚项。

进行润滑计算时，将Reynolds方程得到的压力代入弹性力学方程求解变形的膜厚，再根据变形的膜厚返回Reynolds方程求解压力，循环迭代，直至获得收敛的压力和膜厚解。

2 数值计算

对于常见的轴承形式，一般采用差分法即可以获得很好的计算结果。本文采用中心差分的格式[11]对(2)式进行离散，对于节点(i，j)上的一阶导数，可用半步长插入点上的P值构成的中心差商近似表达为：

(5)

至于(i，j)上的二阶导数，用相邻半步长插入点上的一阶导数的中心差商表示为：

(6)

将以上差分格式代入(2)式，这样，正常工况、等温、不可压缩油膜的无量纲Reynolds方程转化为：

Ai,jPi+1,j+Bi,jPi-1,j+Ci,jPi,j+1+Di,jPi,j-1+

Ei,jPi,j=Fi,j

(7)

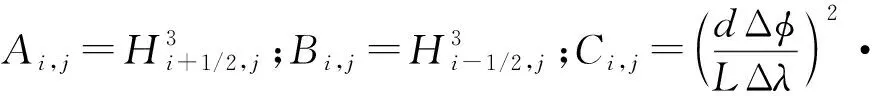
Ei,j=Ai,j+Bi,j+Ci,j+Di,j;Fi,j=Δφ(Hi+1/2,j-Hi-1/2,j)。

得到程序编制中的压力迭代公式为：

(8)

求解需要在给定的边界条件下进行，本文分析采用Reynolds边界条件[12]。

3 弹性变形的有限元求解

ANSYS有限元软件的结构分析模块可以方便有效地进行弹性变形问题的求解。通过施加径向外载荷和设置边界条件，可求出对应的弹性变形量。为了协调有限差分法和有限元法，在轴颈外表面沿轴向和径向采用相同数目的网格进行划分，滑动轴承分析模型轴颈外表面节点数为25×25。

将有限差分法求解得到的油膜压力作为外载荷施加到轴颈外表面，同时采用轴颈一端面固定，另一端面简支的边界条件，计算出轴颈外表面对应节点的弹性变形量，然后将每一迭代过程中得到的弹性变形矩阵返回差分法求解Reynolds方程中进行耦合迭代，直至满足迭代收敛精度为止。整个过程使用ANSYS参数化设计语言编写程序，从而智能地求解复杂的弹性变形及迭代循环过程。

4 实例分析

以下通过一具体实例对径向滑动轴承的润滑特性进行分析，来验证所提出耦合算法的正确性，并在此基础上探讨重载工况下轴颈在轴向两端磨损严重的原因。表1为径向滑动轴承算例的主要计算参数。

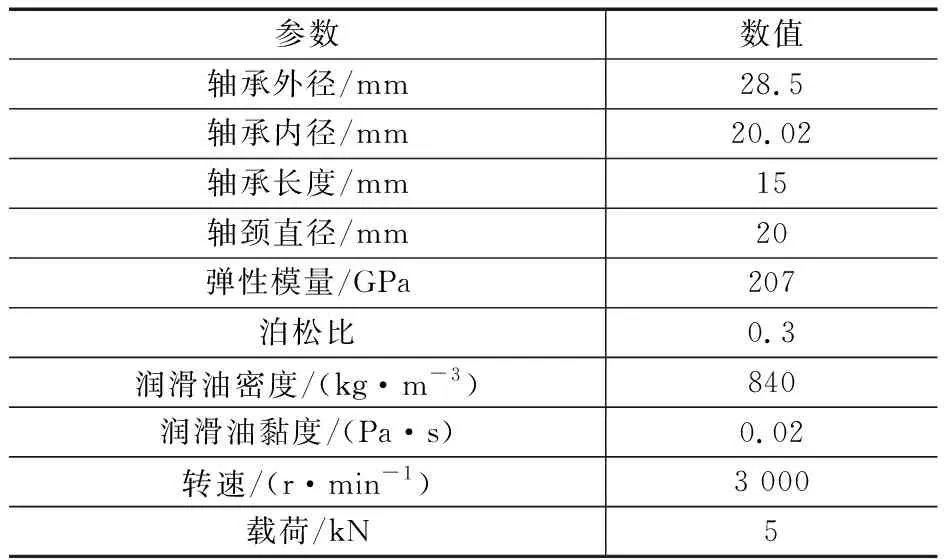
表1 径向滑动轴承主要计算参数

4.1 油膜压力分布

径向滑动轴承考虑弹性变形和不考虑弹性变形时油膜压力分布如图1和图2所示。对比图1与图2可知：考虑弹性变形时轴承的最大油膜压力比不考虑弹性变形的情况有大幅度的下降，下降幅度超过了50%。在轴承轴向方向，考虑弹性变形时油膜压力分布比较扁平，而在两端急剧下降；不考虑弹性变形的轴承轴向压力分布接近于抛物线；另外，在圆周方向，考虑弹性变形的轴承承载区域更大，大概比不考虑弹性变形的轴承的承载区域大7%。

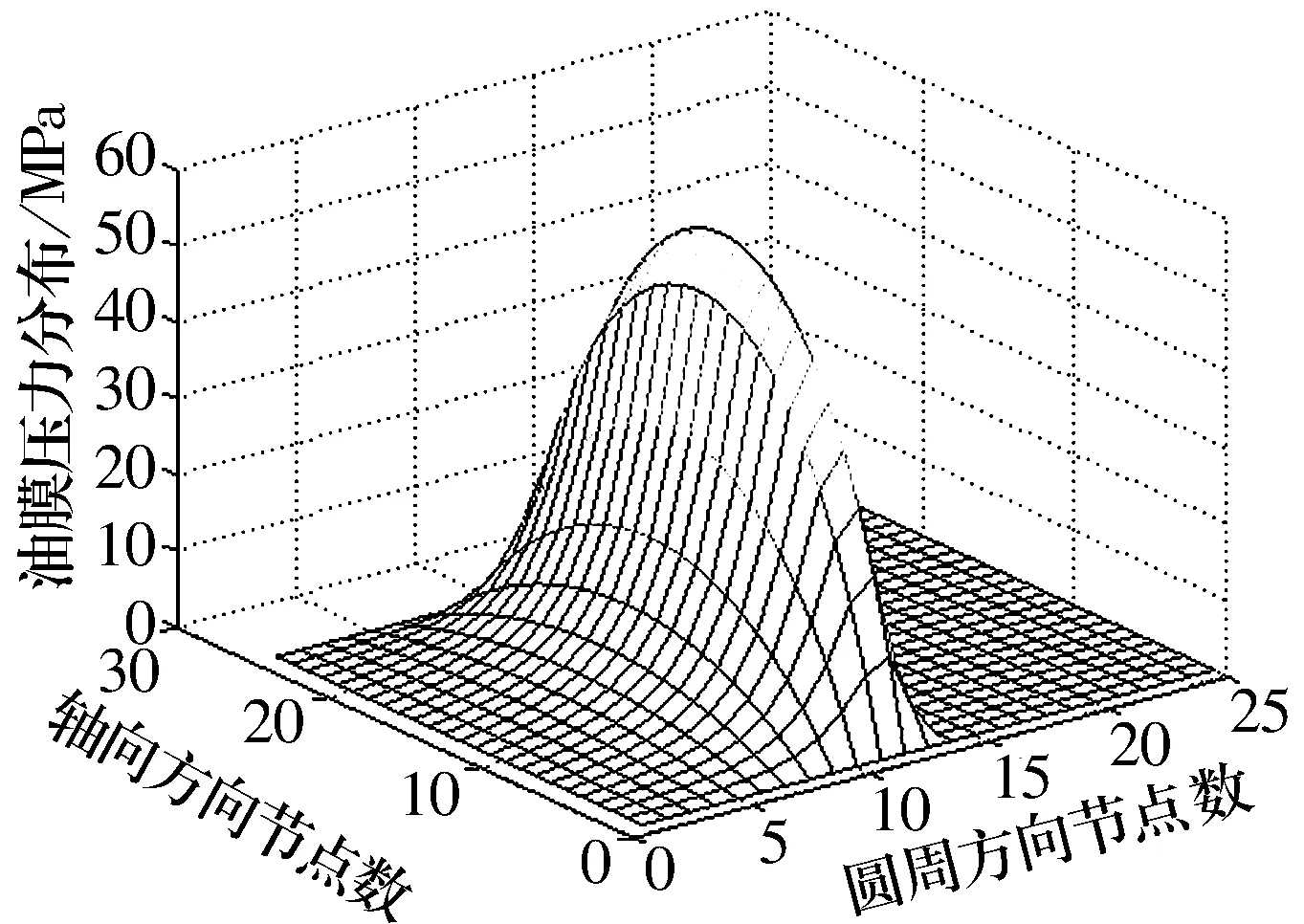
图1 不考虑弹性变形时油膜压力分布

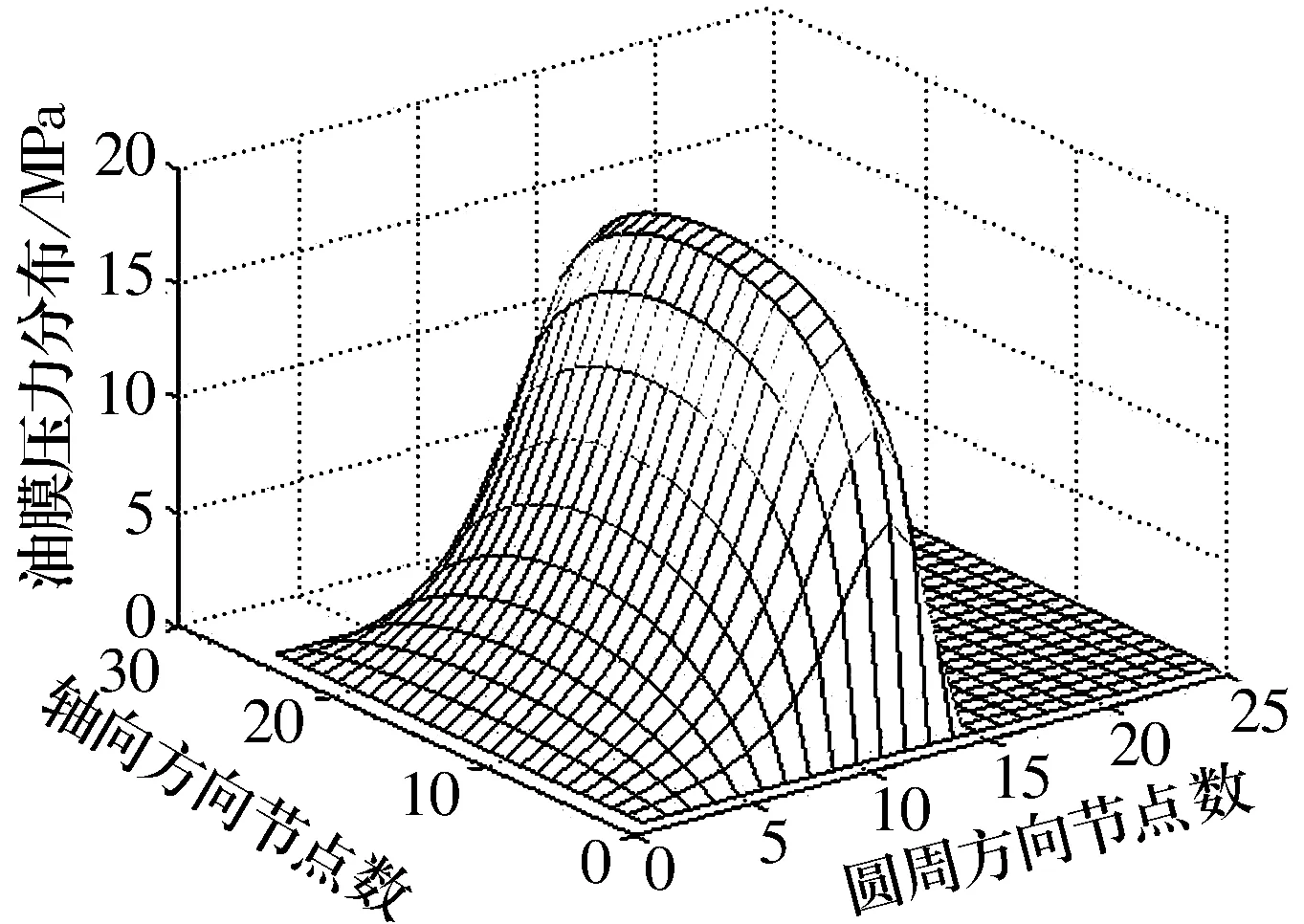
图2 考虑弹性变形时油膜压力分布

4.2 油膜厚度分布

径向滑动轴承考虑弹性变形和不考虑弹性变形时油膜厚度分布如图3和图4所示。对比图3和图4可知，考虑弹性变形的油膜厚度分布与不考虑弹性变形的油膜厚度分布有很大区别。在轴承的轴向方向，油膜厚度不再相等，轴承中间部位的油膜厚度比两端的要大。这意味着在轴承两端轴颈与轴瓦间隙比较小，间隙的尺寸与轴承摩擦副磨屑的尺寸差不多；因而导致轴承两端轴颈产生剧烈的磨粒磨损，使得两端的磨损量比中间的磨损量大。同时，考虑了弹性变形的轴承的最小油膜厚度大概为5 μm，最大油膜厚度大概为26 μm；而不考虑弹性变形时轴承的最小和最大油膜厚度分别为2 μm和18 μm。图5和图6分别为考虑弹性变形和不考虑弹性变形时轴承中部横截面的油膜分布。由图5和图6知，在轴承圆周方向上，考虑弹性变形时中部横截面的油膜不再呈对称分布，承载区油膜厚度的下降更加缓慢，且最小油膜厚度值所对应的角度加大。

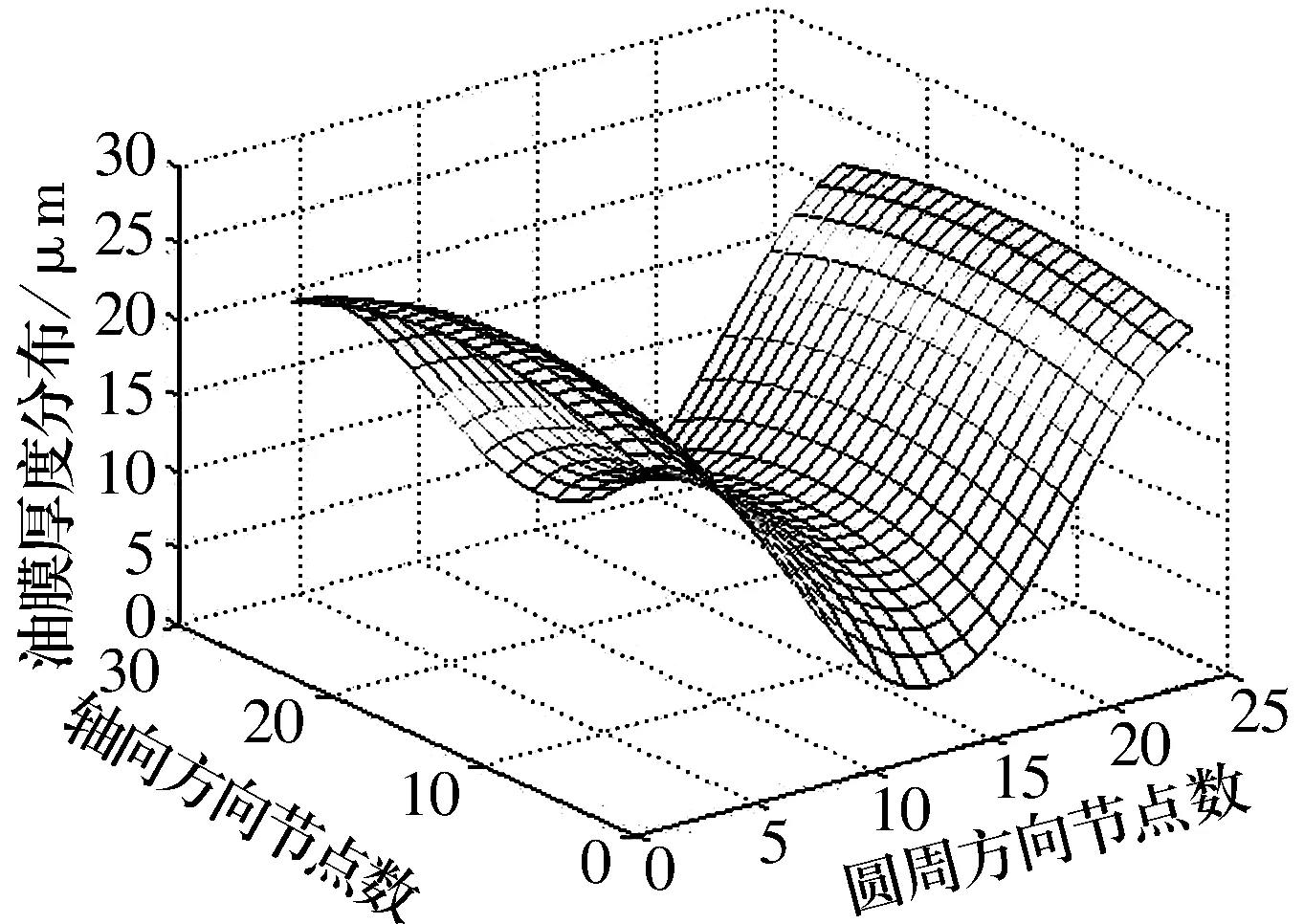
图4 考虑弹性变形时油膜厚度分布

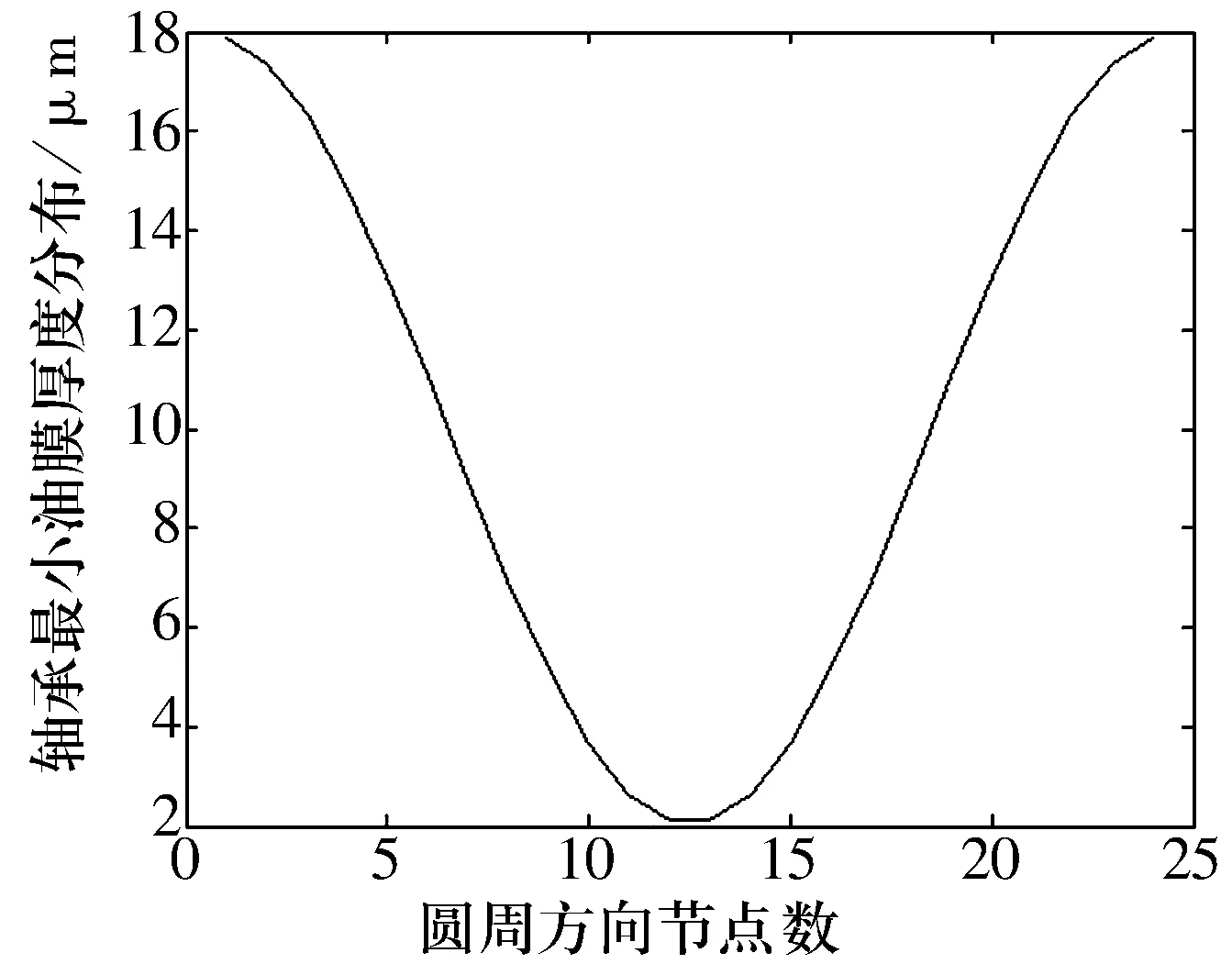
图5 不考虑弹性变形时中部横截面油膜分布

图6 考虑弹性变形时中部横截面油膜分布

4.3 轴颈弹性变形

图7为轴颈在油膜压力作用下发生弹性变形的轮廓，为了更有效地对弹性变形进行分析，对各节点的弹性变形量进行整理并获得如图8所示的弹性变形量分布。由图8可知，轴颈的弹性变形量达到15 μm左右，非常接近不考虑弹性变形的刚性轴承的最大油膜厚度值。这说明轴承弹性变形量会对其润滑性能产生很大的影响，不能忽略，特别是在重载或低弹性模量材料的情况下。

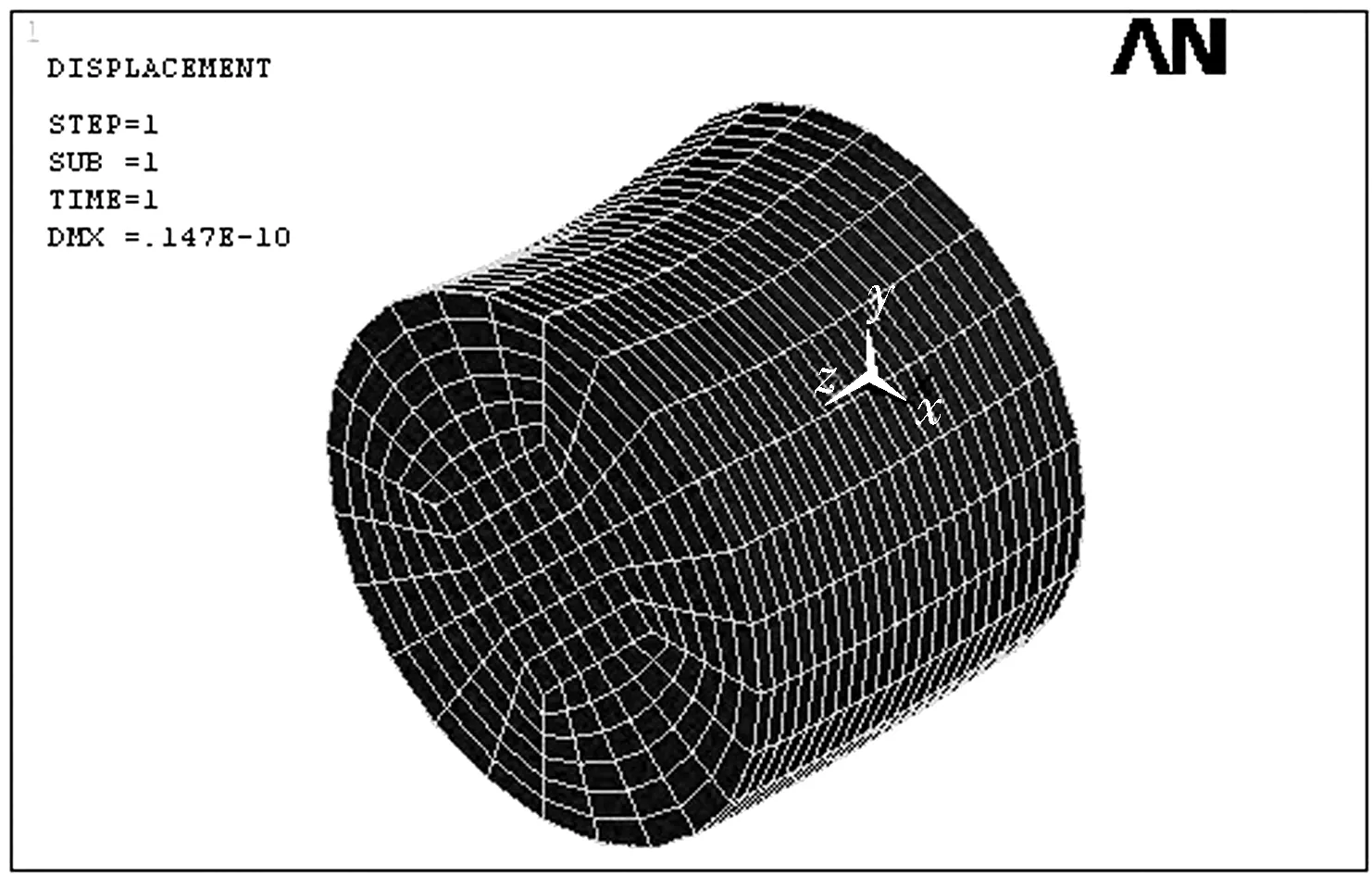
图7 轴颈弹性变形轮廓

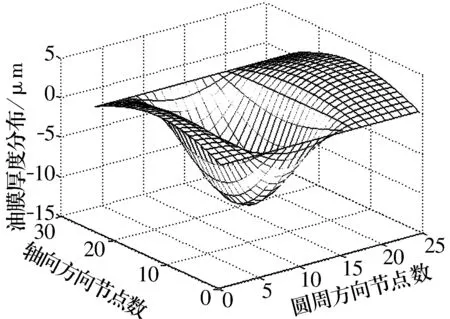
图8 轴颈弹性变形量分布

5 结束语

径向滑动轴承弹流润滑耦合算法可以准确有效地求解滑动轴承弹流润滑问题。通过实例分析可知，考虑轴承弹性变形的润滑油油膜压力峰值减小，但油膜压力承载区域增大，从而保证了轴承的承载能力。同时，在油膜压力的作用下轴承表面发生弹性变形，致使油膜厚度明显增大。在轴承轴向方向，油膜厚度呈现中间部位油膜厚度大，两端油膜厚度小的特点。这使得轴颈两端易发生磨粒磨损，从而降低轴承的使用寿命。为此，可对轴颈两端修形以减少磨粒磨损的影响，这对轴承的结构设计提出了新的问题，也为轴承的减磨与提高寿命提出了新思路。