径向载荷作用下高速交叉滚子轴承的载荷分布

张 钢，刘 莹，刘汝卫，阮 娟，殷庆振

(上海大学 轴承研究所，上海 200072)

交叉滚子轴承既可以承受径向载荷，又可以承受轴向载荷，还可以承受倾覆力矩，能够满足许多工业应用的承载要求。

文献[1]指出了交叉滚子轴承现有隔离块设计方法的缺陷，并提出了设计改进方案；文献[2]对交叉圆锥滚子轴承的制造进行了深入探讨；文献[3]则对交叉滚子轴承的返修过程进行了详尽的介绍；文献[4]在交叉滚子轴承的滚子与滚道间隙测量方面做了实践研究。但目前对交叉滚子轴承进行深入理论研究的文献较少，多数只限于对生产实践经验的总结。本文在考虑滚子离心力的情况下，对承受径向载荷的高速交叉滚子轴承的载荷分布进行了分析。

1 轴承结构

交叉滚子轴承的结构比较特殊，圆柱滚子在呈90 °的V形沟槽滚动面上相互垂直交叉地间隔排列，滚子间由一个隔离块隔开，如图1所示。

图1 交叉滚子轴承结构

2 滚子的受力分析

高速运转的交叉滚子轴承承受径向载荷Fr作用时，其滚子的受力如图2所示，其中，z轴为轴承的旋转轴线，xOy为轴承的径向平面。图2中Qij，Qij+1分别为内圈对滚子A，B的作用力；Pij，Pij+1分别为内圈对滚子A，B作用力的径向分力；Qoj，Qoj+1分别为外圈对滚子A，B的作用力；FcA，FcB分别为滚子A，B的离心力。

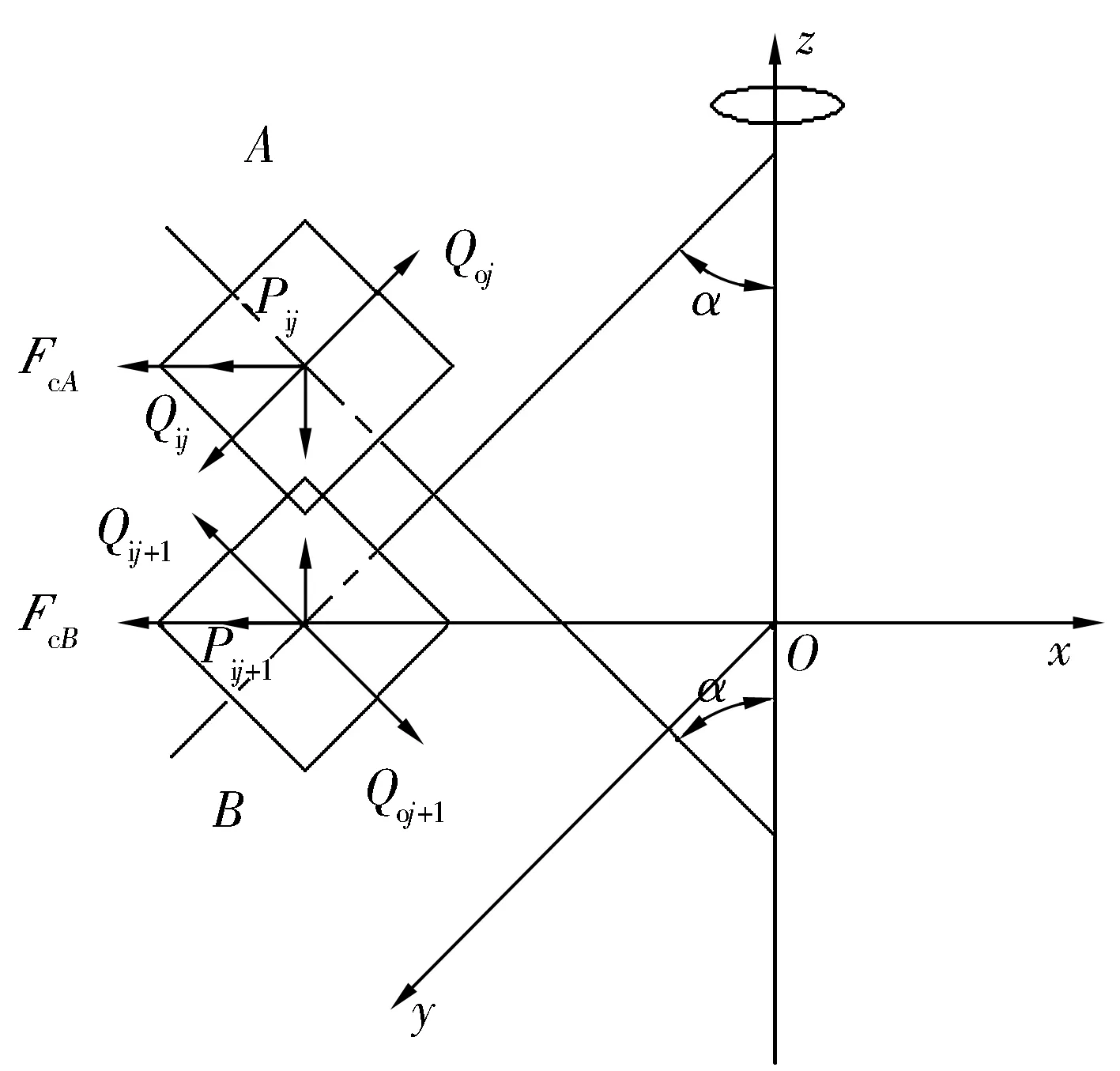
图2 滚子受离心力作用时径向载荷示意图

对任一滚子有平衡方程：

Qoj-Qij-Fccosα=0，j=1，2，…，Z

(1)

式中：Qoj为外圈对滚子的作用力；Qij为内圈对滚子的作用力；Fc为滚子离心力；α为内滚道和滚子的接触角，α=45°；Z为滚子数。

因经典轴承理论中滚子离心力的推导并没有对滚子形状作出限制，这里也可以适用，则绕轴承轴线旋转的钢制滚子的离心力Fc为

(2)

式中：Dw为滚子直径；lt为滚子长度；Dpw为滚子组节圆直径；nm为滚子的公转速度。

3 滚子的载荷分布

图3为交叉滚子轴承载荷分布示意图。设滚子的位置角为θj，受载最大的滚子的位置角为θ1(θ1=0)，则内圈在径向的受力平衡方程为：

(3)

图3 交叉滚子轴承载荷分布示意图

图2中，任一θj和θj+1处的滚子存在：

Pij=Qijcos (-α)

(4)

Pij+1=Qij+1cosα

(5)

以此类推，轴承的径向载荷Fr与各滚子载荷之间的受力平衡方程为:

(6)

根据Hertz弹性理论，滚子与套圈滚道接触时的变形量与载荷的关系为:

Q=Kδn

(7)

则，(1)式和(6)式变为:

(8)

(9)

式中：δoj为任一滚子和外圈滚道间的弹性变形量；δij为任一滚子和内圈滚道间的弹性变形量；K为载荷-位移常数，K=7.86×104l8/9。

在载荷作用下，滚子与套圈的接触变形量等于滚子分别与内、外滚道接触变形量之和，即:

δrj=δij+δoj

(10)

式中：δrj为任一滚子与套圈的接触变形量。且考虑径向游隙Gr(Gr=-0.01～0 mm)，则存在:

(11)

式中:δr为θ1=0时套圈的径向位移；θj为滚子的位置角。

由(8),(10)和(11)式得:

(12)

然后用Newton-Raphson方法联立求解(9)式和(12)式，得到δr和δij，最后得到套圈对滚子的作用力为：

(13)

(14)

4 Matlab实例计算

根据以上理论分析，以设计生产的交叉滚子轴承KBCB060-A为例，编制Matlab程序，计算轴承的设计参数对轴承载荷分布的影响。该轴承的主要参数如表1所示。

4.1 转速对载荷分布的影响

表1中其他的参数不变，分别选取n为6 000，10 000，25 000，40 000，55 000 r/min，编制Matlab程序，得到图4结果。

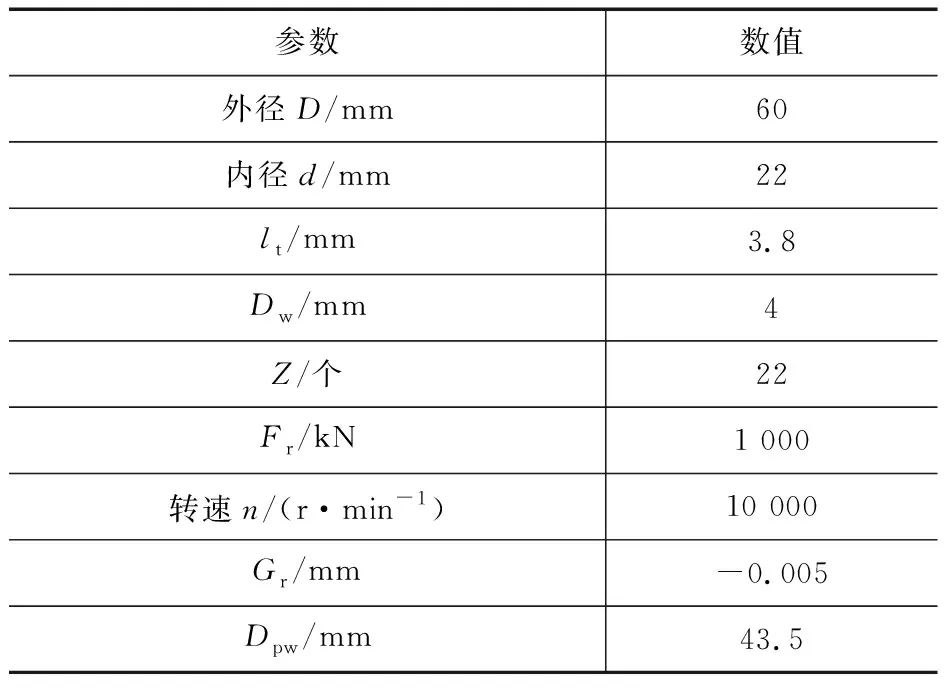
表1 KBCB060-A轴承的主要参数

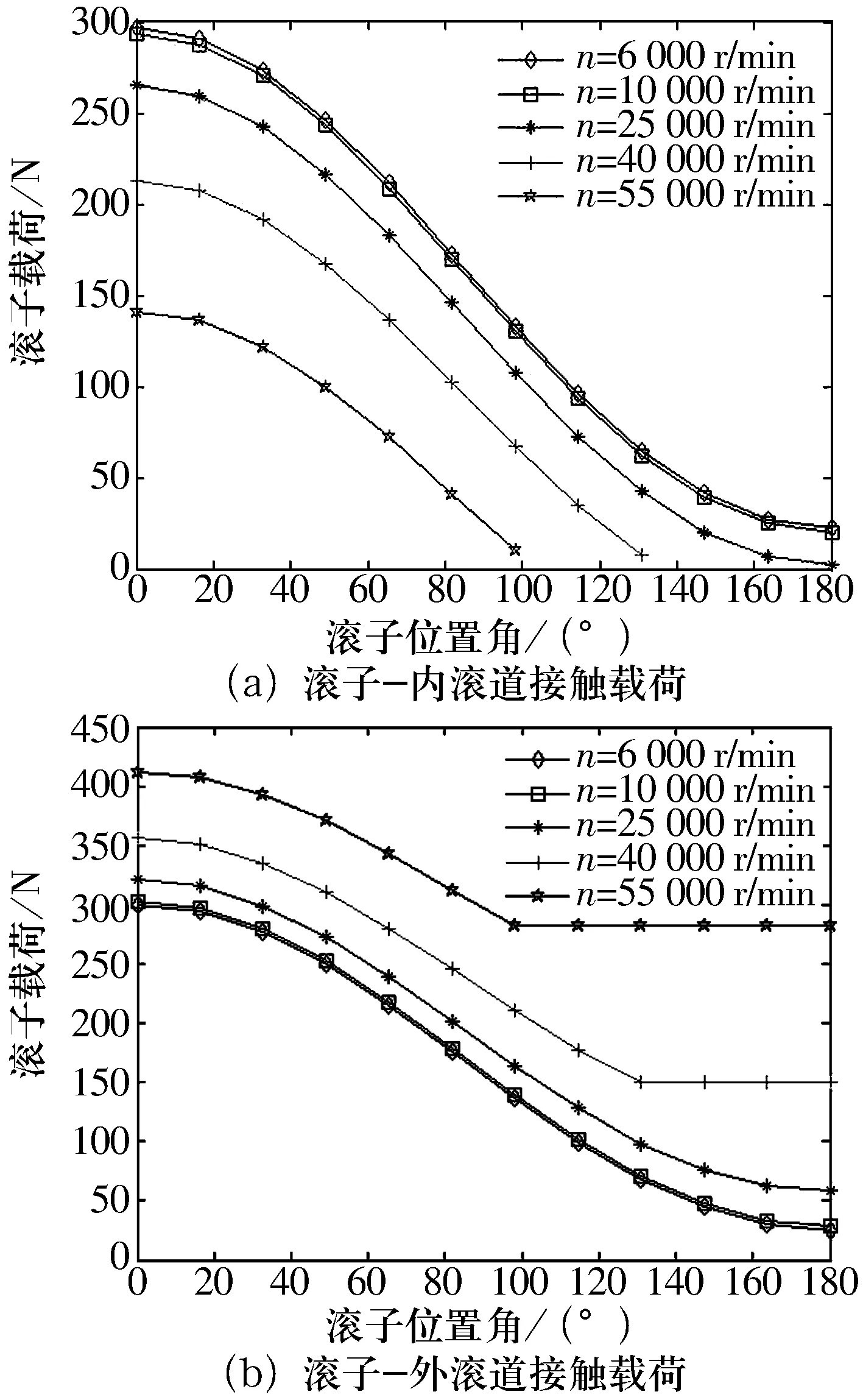
图4 转速变化对滚子载荷分布的影响

从图4可以看出：当n低于10 000 r/min时，由于离心力较小，n对滚子的接触载荷影响较小，可以忽略不计。但当n高于10 000 r/min时，n对滚子的接触载荷影响较大。由于滚子离心力的影响，内滚道作用于滚子的载荷逐渐减小，而外滚道作用于滚子的载荷逐渐增大；随着转速的提高，内滚道与滚子的接触区域逐渐减小，滚子载荷分布的不均性不断加大，而外滚道与滚子的接触区域影响不大。当n达到55 000 r/min时，由于离心力的作用，内圈滚道作用于滚子的最大接触载荷由300 N减小到了150 N，减小了50%；与此同时，由于平衡载荷的需要，外圈滚道作用于滚子的接触载荷则相应增加了50%，但在滚子位置角为100°处时，内圈作用于滚子的接触载荷变为0，滚子与内圈开始分离，外圈作用于滚子的接触载荷则恒为滚子的离心力，因而影响到轴承的使用寿命，因此在高速情况下需要考虑离心力对轴承载荷分布的影响。

4.2 径向外载荷对载荷分布的影响

表1中其他参数不变，分别选取径向外加载荷1 000，2 000，3 000，4 000，5 000 N，编制Matlab程序，得到图5结果。

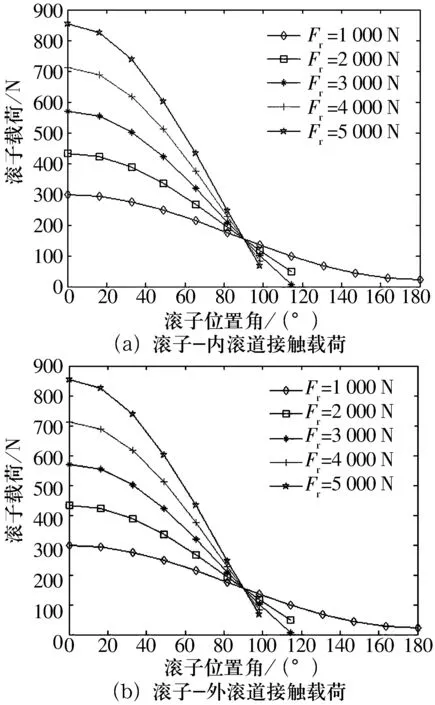
图5 外加载荷的变化对载荷分布的影响

从图5可以看出：随着径向外载荷的逐渐增大，内、外圈滚道作用于滚子的载荷均逐渐增大，但滚子与内、外滚道的接触区域均逐渐变小，即滚子受载不均匀性增大。当Fr=1 000 N时，滚子承受的最大载荷和最小载荷之差为250 N左右；当径向外载荷Fr增大至5 000 N时，滚子所受的最大载荷为850 N左右，滚子所受最大载荷和最小载荷之差达到了800 N左右。因此，径向外载荷的增大不仅使滚子承受的最大载荷增大，而且使滚子所受载荷的不均匀性也变大。这种变化趋势与Harris对圆柱滚子轴承的分析基本一致，恰好证明了本文对交叉滚子轴承理论分析的正确性。所以在设计交叉滚子轴承的过程中要考虑外载荷对滚子载荷分布的影响。

4.3 径向游隙对载荷分布的影响

表1其他参数不变，分别选取游隙Gr为-0.002，-0.004，-0.006，-0.008，-0.01 mm，编制Matlab程序，得到图6结果。

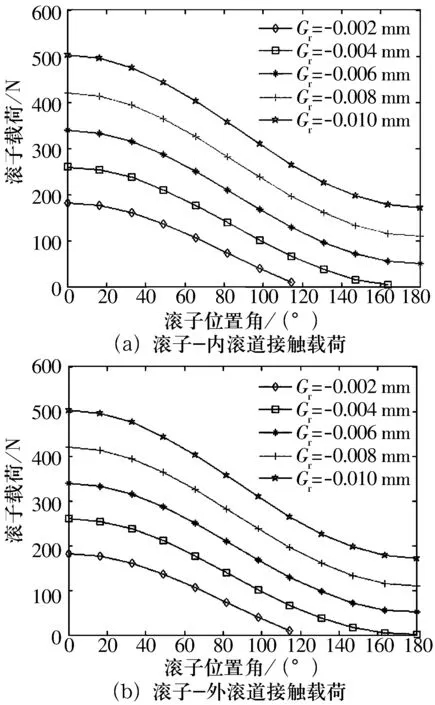
图6 径向游隙的变化对载荷分布的影响

从图6可以看出：随着轴承游隙的减小，轴承内圈和外圈对滚子的接触载荷均变大。当游隙Gr由-0.002 mm减小到-0.010 mm时，内、外圈滚道作用于滚子的最大接触载荷由181 N增大到了502 N，增加了1.7倍，可见，游隙对轴承载荷分布的影响不可忽略。值得注意的是，当轴承负游隙值较大时，滚道与滚子间的接触受力区域明显减小，载荷分布也不均匀。

5 结论

(1)当n低于10 000 r/min时，转速对载荷分布的影响变化较小，可以忽略不计。但当n高于10 000 r/min时，转速对载荷分布影响较大，需要考虑离心力对轴承载荷分布的影响。随着转速增大，滚子与内滚道的接触受力区域逐渐减小，而滚子与外滚道的接触受力区域变化不大。

(2)随着轴承外载荷的增大，不仅最大受载滚子的接触载荷增大，滚子所受载荷的不均匀性也变大。所以在设计轴承的过程中应考虑外载荷对滚子接触载荷分布的影响。

(3)随着轴承游隙的减小，滚子所受的载荷增大。当轴承负游隙值较大时，滚道与滚子间的接触受力区域明显减小，载荷分布也不均匀，轴承游隙对于轴承载荷分布影响不可忽略。

本文的分析结果主要为高速交叉滚子轴承的结构优化设计中参数的确定提供依据。值得注意的是，由于其都是在其他参数不变、不考虑摩擦、温升的前提下进行的，并不能完全反映轴承的实际载荷分布状况。