重载下调心滚子轴承接触应力分析及凸形设计

李思成，陈晓阳，陈爱华，马纯青

(1.上海大学 机械自动化系，上海 200072；2.上海联合滚动轴承有限公司，上海 200240；3.杭州劳格罗拉轴承滚子有限公司，杭州 310013)

1 前言

调心滚子轴承具有接触区域长度较长的特点，因此具有很大的承载能力，并且其还可以适应由于轴的安装、制造误差、变形等带来的偏斜。

在滚动轴承的接触问题分析中，由于Hertz接触理论能得到较为符合实际工况的结果而得到广泛应用。Hertz接触变形理论对于点接触和线接触的接触变形求得了精确的理论解。对于点接触，当弹性体表面可以近似地以二次曲面表示时给出了问题的全部解，而对于线接触只给出了部分解[1]。对于一般的圆柱滚子轴承，Lundberg于1939年提出了著名的Lundberg对数凸形公式，给出了最佳凸度曲线——对数素线。但是对于调心滚子轴承，由于其特殊的几何形状，目前还不能对圆弧素线做像对数素线这样的修形。文献[2]指出轻载时调心滚子轴承中滚子和滚道为点接触，当作用在轴承上的载荷超过点接触的极限时为线接触，该极限为接触区域长轴的长度大于滚子的有效长度。实际上只有当接触区域长度远大于宽度的时候才接近线接触。随着施加载荷的增大，滚子和滚道的接触区域会变成如图1所示阴影部分的形状，这是因为当载荷增大到一定值时，接触区域长度会达到滚子的有效长度，如果载荷继续增大则接触区域只能向宽度方向增大，而滚子端部修形部分比中间增大更快，应力值也迅速增大，这种接触区域已经超出了Hertz理论解的范围。

图1 重载时实际接触区域

文献[3]利用切片法对单列角接触调心滚子轴承进行了应力分析，由于切片法忽略了相邻两个切片之间的影响，因此不能正确反映滚子端部的应力集中；文献[4]提出一种一边圆弧素线一边对数素线相结合的滚子轮廓，但这种滚子轮廓同时要求内、外圈滚道做相应的修形，在现有的加工技术水平上很难实现，并且没有给出这种轮廓与相应的滚道接触应力分布；文献[5]利用有限元法分析了4种表面形状的滚子(直素线、圆锥倒角、圆弧倒角、全圆弧素线)和平面接触情况下滚子的接触应力；文献[6-7]将影响系数法同Boussinesq J半空间体力-变形结合起来求出一般表面轮廓的接触问题；文献[8]利用数值法编写FORTRAN程序计算了5种表面形状(直素线、对数素线、全圆弧素线、相交倒角直素线、相切倒角直素线)的滚子和平面接触情况下滚子的接触应力。以上文献对于调心滚子轴承的应力计算都是将接触情况简化为滚子和平面的接触，这与实际接触情况有一定差别，另外，没有考虑到滚子的端部修形部分对接触应力的影响，因此在重载情况下，有必要对调心滚子轴承的轮廓做进一步研究。

2 弹性接触理论方程

根据文献[9]，设任意表面的两光滑弹性体起始接触于点O，并以该点为圆心建立直角坐标系，如图2所示，M，N两点坐标为(x,y,z1)，(x,y,z2)。

图2 两弹性体接触模型

施加外力P后，弹性体发生变形，起始接触点扩展为一接触区域Ω，变形后弹性体上的点服从位移方程：

(1)

式中：δ为两弹性体接触的弹性趋近量；ω1，ω2为M，N两点在相应z坐标轴方向的变形。

当变形在弹性范围内时，根据Boussinesque[1]解，弹性体变形可表示为：

(2)

式中：k为材料常数；E为材料弹性模量；ν为泊松比。

将(2)式带入(1)式可得在Ω内一般的光滑弹性接触问题的主导方程——Fredholm积分方程为：

(3)

同时，接触应力p(x,y)应该满足平衡条件和物理条件：

(4)

这样，根据弹性体的几何形状、材料常数和外力p，由(3)式就可以求出接触区域Ω，弹性趋近量δ以及接触应力p(x,y)。

3 弹性接触的数值解法

利用影响系数法，假设一矩形接触区域Ω1，Ω1要大于实际接触区域Ω，将Ω1划分为j×i个矩形单元，并假定接触应力在各单元上均匀分布。以pj表示单元j上的接触应力，以单元i的中心(xi,yi)处弹性体表面的原始距离为该单元的表面函数离散值Si，则(3)式可在Ω1上离散为一组n+2阶的线性代数方程组：

(5)

式中：Fij为影响系数。

(6)

根据平衡条件将(4)式离散化为：

(7)

式中：Aj为Ω1区域上离散后的单元面积，由(5)式和(6)式建立弹性体接触问题的主导线性方程组，以矩阵形式表示为：

BP=S

(8)

式中：

(9)

(10)

(11)

根据以上分析过程，编制FORTRAN程序求解矩阵方程，流程如图3所示。

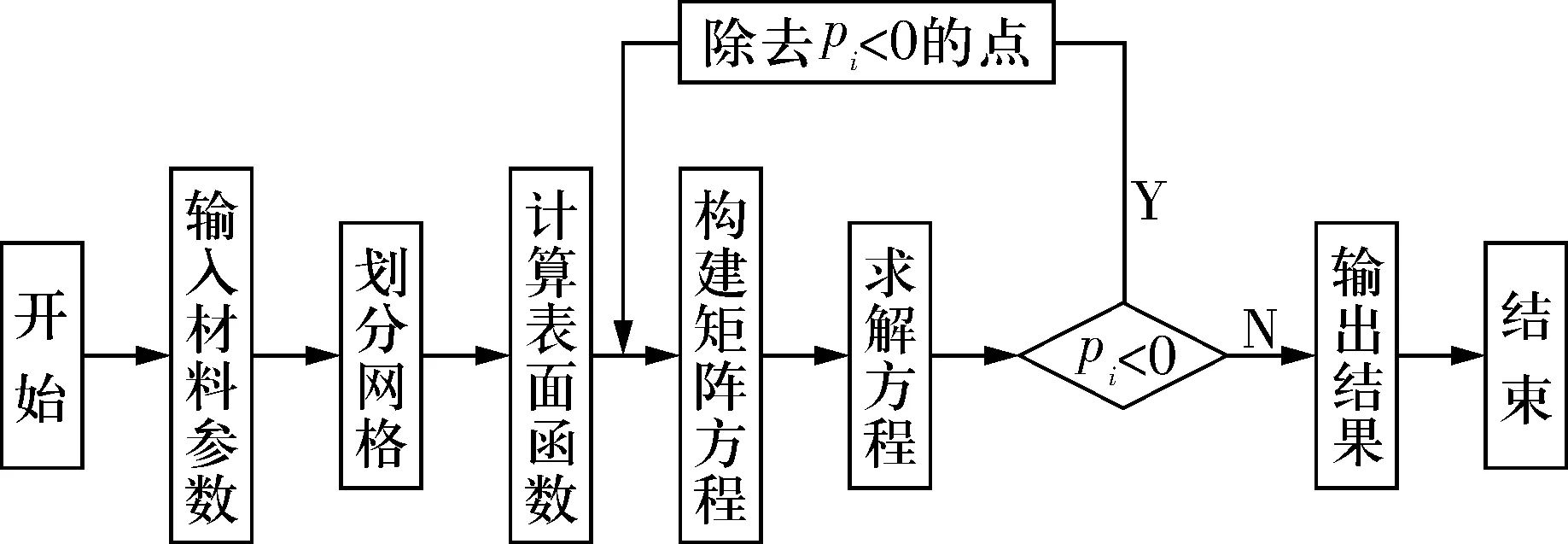
图3 程序流程图

4 轴承的应力分析

以某公司生产的型号为23156CA轴承(图4)为例进行计算，其主要几何参数如表1所示，轴承材料为GCr15SiMn，弹性模量E=2.08 GPa，泊松比ν=0.3，滚子数目为2×21，接触角为11.3°，滚子为双排错位排列。

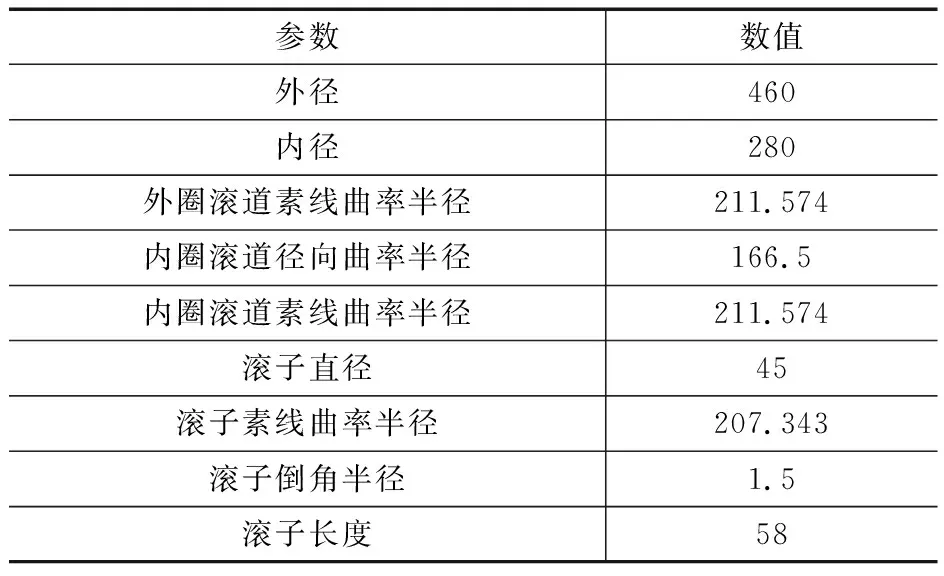
表1 轴承几何参数 mm

图4 调心滚子轴承23156CA

4.1 程序正确性验证

当对轴承施加一较小的载荷时，接触区域为一椭圆，因此可以利用Hertz理论验证该程序的正确性，Hertz解基于文献[10]中公式计算得到。为了保证计算结果的精确性，滚子和滚道接触区域宽度和长度方向划分为20×100个网格。对受力最大的滚子施加Q=50 kN的力，所得到的接触应力如图5所示，计算结果对照表2，可以看出与Hertz解相比较，该数值方法计算的结果相差很小，因此程序的结果是正确的。

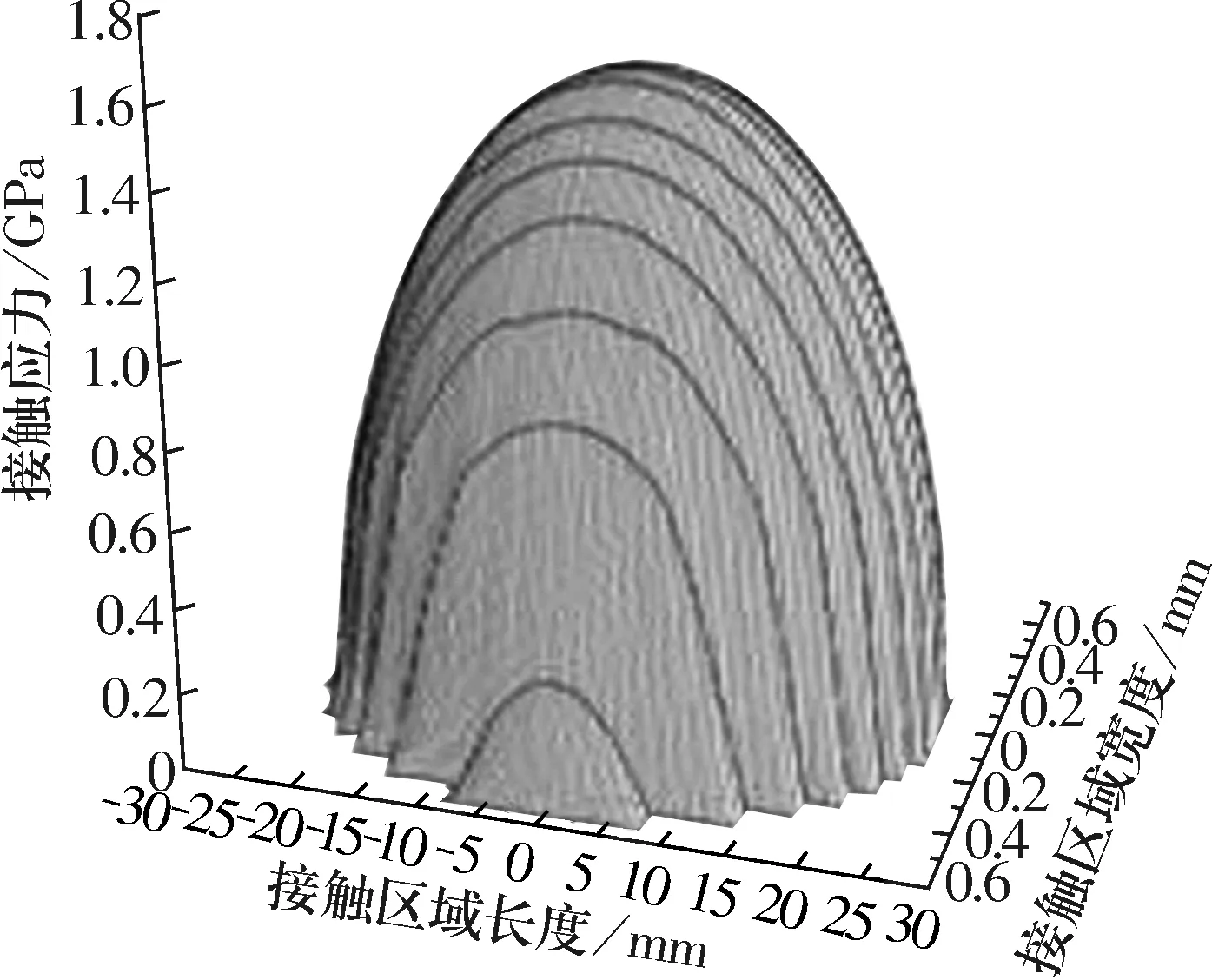
图5 施加50 kN时滚子-内圈接触应力分布

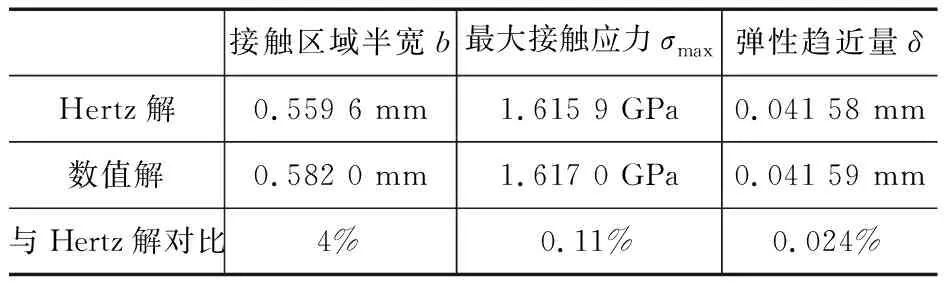
表2 数值解与Hertz解对比

4.2 原设计几何尺寸及技术要求下的计算

该轴承所设计的径向基本额定动载荷为Cr=2 200.3 kN，对于正常径向游隙的滚子轴承，受力最大滚子载荷可根据(12)式计算。

(12)

根据文献[10]得Jr=0.457 7，将Fr分别取0.15Cr，0.2Cr，0.3Cr，0.5Cr，0.7Cr值可算得Qmax分别为35，46.7，70，116.7，163.4 kN。以内圈和滚子的接触为例，在程序中施加几种载荷计算结果如图6所示。

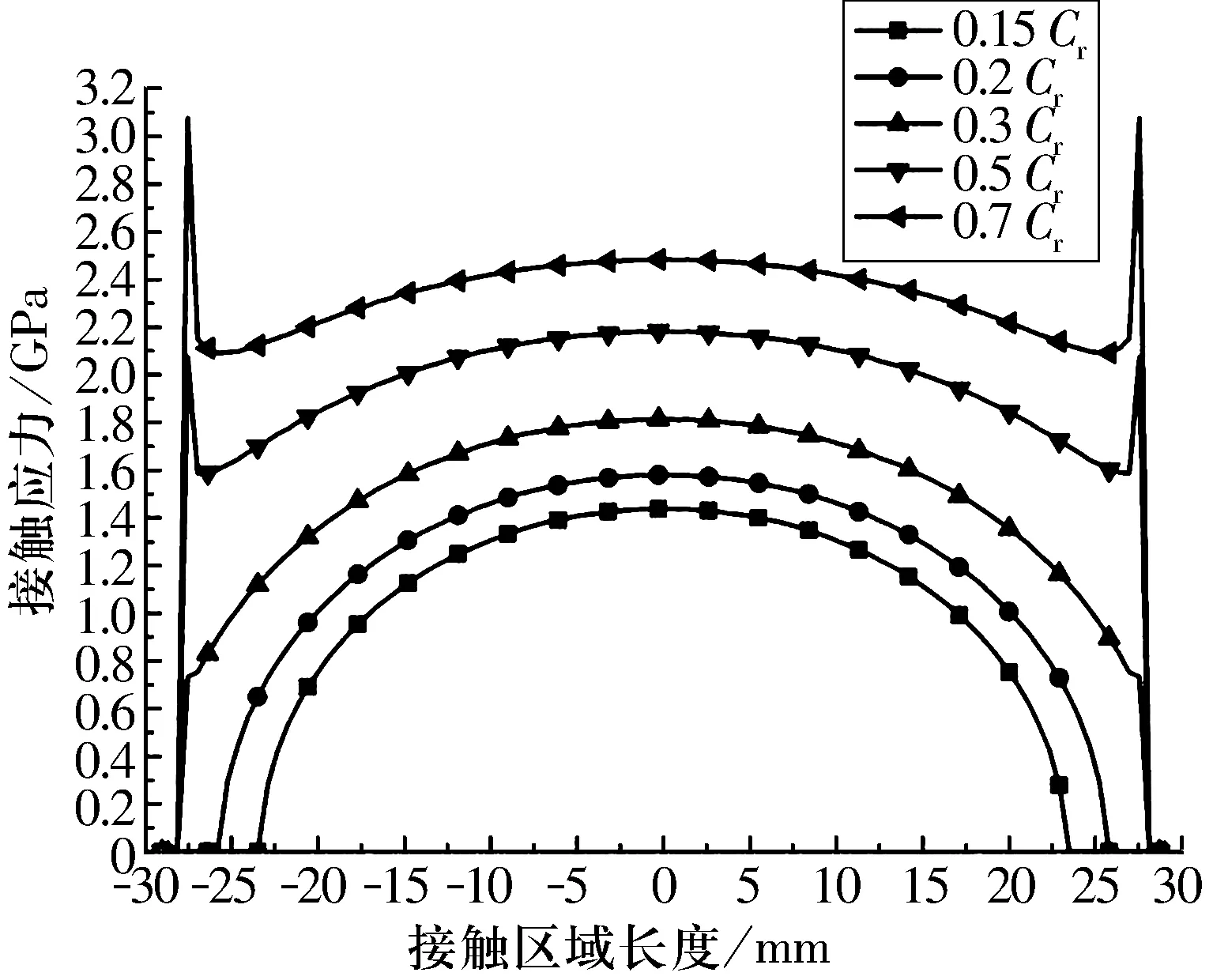
图6 0.15～0.7Cr时受力最大滚子-滚道接触应力分布

由图6可以看出，随着载荷的增大，接触应力和接触区域增大。当施加载荷为0.15Cr时，滚子和滚道的接触区域长度只有46.4 mm，只占滚子有效长度的83.8%，有16.2%的滚子有效长度没有用到；当载荷增加到0.2Cr时，接触区域长度为51.04 mm，占滚子总长度的92%，仍然有8%的滚子有效长度没有利用。一般情况下轴承的重载是指0.15～0.2Cr，但是通过计算得出该轴承即使在0.2Cr下滚子仍然有部分长度未利用，造成了材料的浪费。当施加0.3Cr的载荷时滚子和内圈的接触区域长度刚好达到滚子的有效长度，当载荷进一步增大时在滚子的倒角处开始出现边缘应力集中；当载荷增加到0.5Cr甚至0.7Cr时边缘应力集中已经很明显，这样滚子的边缘部分很容易因疲劳而失效。由图7载荷为0.5Cr时滚子-滚道应力分布可以看出，调心滚子轴承的接触区域既不是椭圆也不是矩形，已经超出了Hertz理论解的范围。

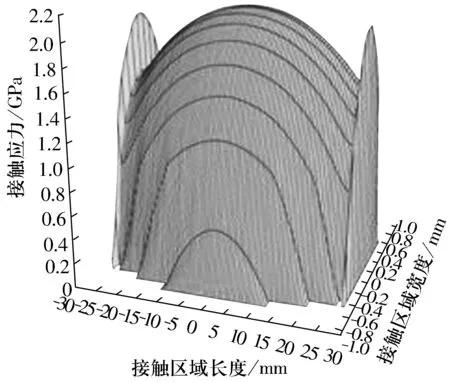
图7 0.5Cr时受力最大滚子-滚道接触应力分布

在一些特殊情况下，例如瞬时冲击或过载，轴承有可能会受到极重载荷的作用，相应的力仍要由滚子来承担。下面从两个方面对滚子进行改进以使滚子既能承受较大的接触应力又不会产生较大的边缘应力集中现象。

4.3 改变滚子与滚道的密合度

根据轴承的原设计尺寸计算出滚子和内滚道素线的密合度Ф=0.98，保持内滚道的曲率半径不变，改变密合度的大小，在载荷为0.5Cr时得到在不同的密合度下滚子-内滚道的接触应力如图8所示。由图可知，随着密合度的减小，边缘应力集中逐渐降低，当密合度Ф=0.965时边缘应力集中现象消失；但在边缘应力逐渐降低的过程中，滚子-内圈接触区域中部的接触应力却在不断增加，在密合度由0.98降至0.965的过程中，接触区域中部的应力由2.182 GPa增加到2.388 GPa。

图8 不同密合度下滚子-内圈接触应力

因此，通过改变滚子与滚道的密合度可以减少或者消除边缘应力集中，但是由于载荷的总量是一定的，边缘应力降低的同时又导致了中间应力的增加。

4.4 滚子倒角的改进

由于滚子倒角和素线交点处的应力集中会在很大程度上减小滚子的寿命，通过改变滚子倒角可以达到降低边缘应力集中的目的。传统的CAD倒角方式是选择两条曲线直接输入倒角半径值，如果在该滚子的设计中采取这种倒角方式，当倒角值过大时，必定会使滚子的中间素线减小，滚子和滚道的接触面也会减小，这样会大大增加滚子中间部分的应力值。倒角改进方式如图9所示，原设计中倒角半径为1.5 mm，实际上两圆弧交点离端面距离为1.3 mm，设该点为c，固定c点将倒角半径值增大。在载荷为0.5Cr时，滚子-内圈密合度为0.98，在滚子端部修形半径R=60 mm时，所得的滚子轴向中间界面上的应力分布情况如图10所示。由图可知，在滚子端部修形半径R=60 mm时，接触区域中间应力没有增大，倒角和滚子素线交点处应力值大大降低，倒角边缘应力值为0。

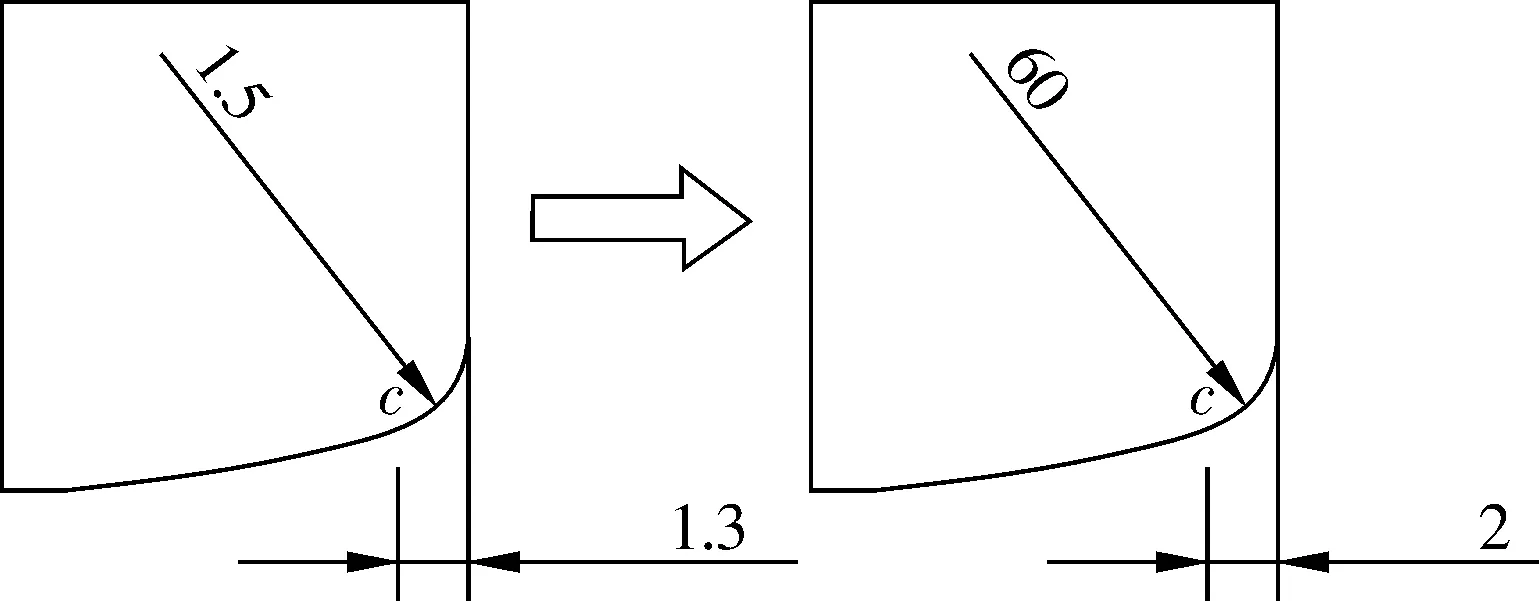
图9 倒角的改进

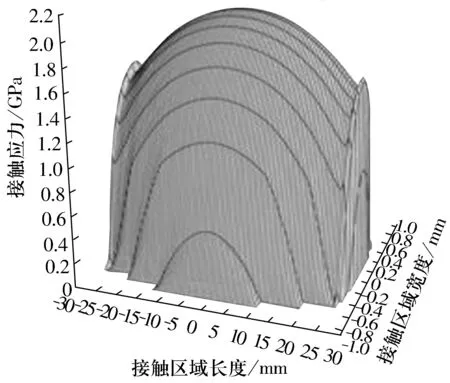
图10 滚子端部修形半径R=60 mm时受力最大滚子-滚道接触应力分布

当滚子端部修形半径增大到120 mm时，滚子-滚道应力分布如图11所示，可以看出边缘应力逐渐变小，变小的趋势要小于接触区域中间的应力，另外接触区域分布也有了较大的改善。

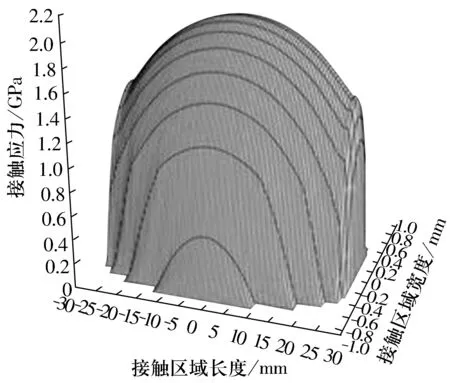
图11 滚子端部修形半径R=120 mm时受力最大滚子-滚道接触应力分布

轴承在重载情况下，理想的滚子-滚道接触情况应该是接触区域长度为滚子的有效长度，在极重载荷或瞬时冲击等特殊载荷条件下，施加在滚子上的载荷会更大，此时设计良好的滚子倒角部分可以起到一定的承载作用。

5 结论

(1) 在轻载情况下，球面滚子与滚道的接触区域为椭圆形，接触状况属于Hertz接触范围，经过计算，得到了和经典的Hertz理论较为一致的解，从而验证了程序的正确性。

(2)在重载情况下，由图7可知接触区域既不是椭圆也不是矩形，超出了Hertz理论的计算范围，此时按照线接触的方式求解表面接触应力是不正确的，利用数值计算方法在这种情况下计算出了球面滚子和内圈滚道的表面接触应力。

(3)对轴承施加0.15Cr载荷时，滚子的有效长度并未完全利用，当载荷增加到0.3Cr时刚好完全利用滚子的有效长度，载荷进一步增加时滚子倒角处开始出现边缘应力集中现象。通过改变滚子和滚道的密合度；采用新的倒角设计方法，并改进滚子倒角处的曲率半径，可使得在极重载荷或者瞬时冲击载荷下，滚子-滚道的边缘集中应力大大减小，接触应力分布也有了较大改善。