钢丝杨氏弹性模量测量的误差分析及改进方法
金玉玲
(天津城市建设学院 基础学科部,天津 300384)
杨氏弹性模量是表征固体材料性质的一个重要物理量,是工程技术中机械构件选材时的重要参数[1].杨氏弹性模量的测量是物理实验中巧妙地利用光杠杆放大法测量微小伸长量的典型实验.实验中所用的测量方法及测量工具较多,数据处理方法典型,通过仪器调整能使学生得到全面的训练,是一个很好的教学实验[2].但是,实验的计算结果较之理论值(2.00~2.10)×1011N/m2有较大的误差[3].笔者通过分析实验产生误差的原因,找出了改进实验的一些可行方法.
1 实验改进前的数据处理
1.1 原始数据
钢丝原长 L=0.798 5,m,镜面到标尺的距离 D,=,1.558 5 m,光杠杆杆长 d,=,0.077 85 m,加减外力后望远镜中标尺读数的变化如表1所示.

表1 加减砝码时望远镜中标尺读数的变化
加外力前钢丝直径 ai(i=1 2 3)的测量结果分别为 0.726,0.728,0.725 mm,千分尺零点读数为+0.010 mm.
通过计算得到:加外力前钢丝直径的平均值a=0.726 mm,修正零点后的直径平均值a′=0.716mm,用逐差法处理数据[4]得到

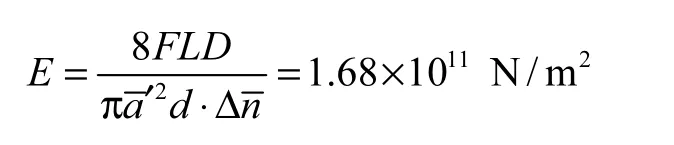
1.2 误差处理
L,D,d三个量为单次测量,用米尺测量L和D,用卡尺测量d,单次测量的标准偏差等于仪器最小分度值的mm.


将上述各测定值及其标准偏差代入相对误差公式,算得 E的相对误差为,E的绝对误差σE=9.7%×1.68× 1011=2× 1010N/m2
1.3 比较各直接测量量引起的误差在总误差中所占的百分数

2 实验改进方法
从各直接测量量的误差在总误差中所占的百分数看,钢丝直径a和用逐差法求得的望远镜中标尺读数的平均值,这两个量对总的相对误差影响最大,要提高测量精度,减小测量误差,使杨氏通性模量 E的测量值接近标准值,必须减小和的值.
2.1 减小的方法
因为给钢丝加相同的力,钢丝的伸长量应相等,可是笔者计算出的望远镜中标尺读数的差值分别为:Δn1=3.18 cm,Δn2=2.62 cm,Δn3=2.53 cm.Δn1与Δn2,Δn3的数值相差很大,其原因是钢丝太粗,砝码盘太轻,不能将钢丝拉直.因此需预加砝码,将钢丝拉直,以减小标尺读数的误差.
2.2 减小的方法
在对钢丝直径的不同位置进行多次测量时,因为钢丝不直或生锈,使得钢丝直径粗细不均匀,不直或生锈处测量值比实际值大,因此增加测量次数,从一组数据中剔除偏差很大的数据,可以减小直径测量的误差.
3 实验改进后的测量结果与分析
针对以上的改进方法,笔者提出了切实可行的操作步骤并通过实验验证了预加砝码的千克数,使得杨氏弹性模量的测量值更接近理论值,减小了测量误差.
3.1 改进后的实验方法
调整好仪器后,先在砝码盘上加 X kg的砝码[6],从望远镜标尺中读数为 n0,然后逐次增加 2.00 kg砝码,分别记下标尺读数 n1,n2,n3,n4,n5,再依次减砝码(每次减 2.00 kg)记下标尺读数 n4′,n3′,n2′,n1′,n0′.计算同一力下标尺读数的平均值,然后用逐差法求,再求E值.
3.2 改进后的实验结果
改进后的实验数据如表2所示.
通过计算可得



表2 改进方法后的测量结果
通过对加力前,在砝码盘上预加 1.00,2.00,3.00,4.00 kg砝码的测量数据的分析,比较改进方法前、后的五个杨氏弹性模量E值和它们的相对误差,可得出结论:当 X =0 kg时(只挂砝码盘,即通常的测量方法),E与理论值相差最大,相对误差也较大.当X=1.00 kg时(预先在砝码盘上加 1.00 kg砝码,改进方法),E1比 E有所增大,但与理论值相差较大,相对误差较大.当 X=2.00 kg时(预先在砝码盘上加2.00 kg砝码,改进方法),E2与理论值差值减小,相对误差较大.X=3.00 kg时(预先在砝码盘上加 3.00 kg砝码,改进方法),E3接近理论值,相对误差明显减小,较合理.X=4.00 kg时(预先在砝码盘上加 4.00 kg砝码,改进方法),E4与E3近似相等,误差也近似相等.考虑到实际情况,砝码盘的长度有限,因此取X=3.00 kg时较合理.
4 结 论
从以上分析可以看出,减小影响最大的两个直接测量量的误差可以使整个实验误差明显减小.通过对本实验的实验方法的改进,减小了和的值,特别是使的值明显减小,使得实验结果与标准值十分接近,实验精度大大提高.
[1] 方利广. 大学物理实验[M]. 上海:同济大学出版社,2006:29-30.
[2] 杨桂娟,梅 妍. 大学物理实验[M]. 大连:大连理工大学出版社,2006:54-58.
[3] 秦先明. 拉伸法测杨氏模量的实验误差分析及其消除方法[J]. 中国科学教育,2005(1):91-92.
[4] 张兆奎,缪连元,张 立. 大学物理实验[M]. 北京:高等教育出版社,2001:63-67.
[5] 杨述武. 普通物理实验[M]. 北京:高等教育出版社,2000:88-90.
[6] 薛晋惠,曾林泽,冉 利. 杨氏模量测量方法的改进[J]. 川北医学院学报,2002,17(4):12-13.

